计算一个神经网络的输出(Computing a Neural Network's output)
计算一个神经网络的输出(Computing a Neural Network’s output)
Note:在编程实现一个神经网络的时候,有一个注意点就是我们要记得保存每一步计算出来的 z z z和 a a a,以及每一步的 d w dw dw、 d b db db等,以便我们进行反向传播。
下图是有一个隐藏层的简单两层神经网络结构:
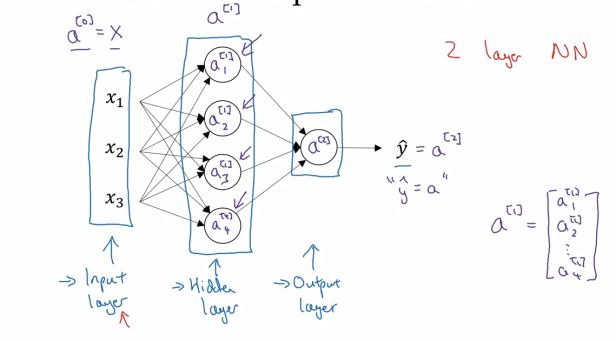
其中, x x x表示输入特征, a a a表示每个神经元的输出, W W W表示特征的权重,上标表示神经网络的层数(隐藏层为1),下标表示该层的第几个神经元。这是神经网络的符号惯例,下同。
神经网络的计算
关于神经网络是怎么计算的,从逻辑回归开始,如下图所示。用圆圈表示神经网络的计算单元,逻辑回归的计算有两个步骤,首先你按步骤计算出 z z z,然后在第二步中你以sigmoid函数为激活函数计算 z z z(得出 a a a),一个神经网络只是这样子做了好多次重复计算。
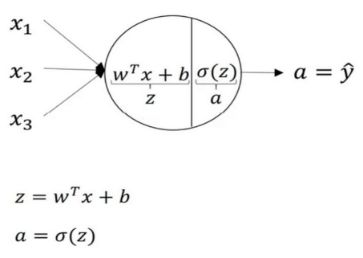
回到两层的神经网络,我们从隐藏层的第一个神经元开始计算,如上图第一个最上面的箭头所指。从上图可以看出,输入与逻辑回归相似,这个神经元的计算与逻辑回归一样分为两步,小圆圈代表了计算的两个步骤。
第一步,计算 z 1 [ 1 ] , z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] z^{[1]}_1,z^{[1]}_1 = w^{[1]T}_1x + b^{[1]}_1 z1[1],z1[1]=w1[1]Tx+b1[1]。
第二步,通过激活函数计算 a 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) a^{[1]}_1,a^{[1]}_1 = \sigma(z^{[1]}_1) a1[1],a1[1]=σ(z1[1])。
隐藏层的第二个以及后面两个神经元的计算过程一样,只是注意符号表示不同,最终分别得到 a 2 [ 1 ] 、 a 3 [ 1 ] 、 a 4 [ 1 ] a^{[1]}_2、a^{[1]}_3、a^{[1]}_4 a2[1]、a3[1]、a4[1],详细结果见下:
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) z^{[1]}_1 = w^{[1]T}_1x + b^{[1]}_1, a^{[1]}_1 = \sigma(z^{[1]}_1) z1[1]=w1[1]Tx+b1[1],a1[1]=σ(z1[1])
z 2 [ 1 ] = w 2 [ 1 ] T x + b 2 [ 1 ] , a 2 [ 1 ] = σ ( z 2 [ 1 ] ) z^{[1]}_2 = w^{[1]T}_2x + b^{[1]}_2, a^{[1]}_2 = \sigma(z^{[1]}_2) z2[1]=w2[1]Tx+b2[1],a2[1]=σ(z2[1])
z 3 [ 1 ] = w 3 [ 1 ] T x + b 3 [ 1 ] , a 3 [ 1 ] = σ ( z 3 [ 1 ] ) z^{[1]}_3 = w^{[1]T}_3x + b^{[1]}_3, a^{[1]}_3 = \sigma(z^{[1]}_3) z3[1]=w3[1]Tx+b3[1],a3[1]=σ(z3[1])
z 4 [ 1 ] = w 4 [ 1 ] T x + b 4 [ 1 ] , a 4 [ 1 ] = σ ( z 4 [ 1 ] ) z^{[1]}_4 = w^{[1]T}_4x + b^{[1]}_4, a^{[1]}_4 = \sigma(z^{[1]}_4) z4[1]=w4[1]Tx+b4[1],a4[1]=σ(z4[1])
向量化计算
如果你执行神经网络的程序,用for循环来做这些看起来真的很低效。所以接下来我们要做的就是把这四个等式向量化。向量化的过程是将神经网络中的一层神经元参数纵向堆积起来,例如隐藏层中的 w w w纵向堆积起来变成一个 ( 4 , 3 ) (4,3) (4,3)的矩阵,用符号 W [ 1 ] W^{[1]} W[1]表示。另一个看待这个的方法是我们有四个逻辑回归单元,且每一个逻辑回归单元都有相对应的参数——向量 w w w,把这四个向量堆积在一起,你会得出这4×3的矩阵。
因此,
公式如下:
z [ n ] = w [ n ] x + b [ n ] z^{[n]} = w^{[n]}x + b^{[n]} z[n]=w[n]x+b[n]
a [ n ] = σ ( z [ n ] ) a^{[n]}=\sigma(z^{[n]}) a[n]=σ(z[n])
详细过程见下:
a [ 1 ] = [ a 1 [ 1 ] a 2 [ 1 ] a 3 [ 1 ] a 4 [ 1 ] ] = σ ( z [ 1 ] ) a^{[1]} = \left[ \begin{array}{c} a^{[1]}_{1}\\ a^{[1]}_{2}\\ a^{[1]}_{3}\\ a^{[1]}_{4} \end{array} \right] = \sigma(z^{[1]}) a[1]=⎣⎢⎢⎢⎡a1[1]a2[1]a3[1]a4[1]⎦⎥⎥⎥⎤=σ(z[1])
[ z 1 [ 1 ] z 2 [ 1 ] z 3 [ 1 ] z 4 [ 1 ] ] = [ . . . W 1 [ 1 ] T . . . . . . W 2 [ 1 ] T . . . . . . W 3 [ 1 ] T . . . . . . W 4 [ 1 ] T . . . ] ⏞ W [ 1 ] ∗ [ x 1 x 2 x 3 ] ⏞ i n p u t + [ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] b 4 [ 1 ] ] ⏞ b [ 1 ] \left[ \begin{array}{c} z^{[1]}_{1}\\ z^{[1]}_{2}\\ z^{[1]}_{3}\\ z^{[1]}_{4}\\ \end{array} \right] = \overbrace{ \left[ \begin{array}{c} ...W^{[1]T}_{1}...\\ ...W^{[1]T}_{2}...\\ ...W^{[1]T}_{3}...\\ ...W^{[1]T}_{4}... \end{array} \right] }^{W^{[1]}} * \overbrace{ \left[ \begin{array}{c} x_1\\ x_2\\ x_3\\ \end{array} \right] }^{input} + \overbrace{ \left[ \begin{array}{c} b^{[1]}_1\\ b^{[1]}_2\\ b^{[1]}_3\\ b^{[1]}_4\\ \end{array} \right] }^{b^{[1]}} ⎣⎢⎢⎢⎡z1[1]z2[1]z3[1]z4[1]⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡...W1[1]T......W2[1]T......W3[1]T......W4[1]T...⎦⎥⎥⎥⎤ W[1]∗⎣⎡x1x2x3⎦⎤ input+⎣⎢⎢⎢⎡b1[1]b2[1]b3[1]b4[1]⎦⎥⎥⎥⎤ b[1]
对于神经网络的第一层,给予一个输入 x x x,得到 a [ 1 ] a^{[1]} a[1], x x x可以表示为 a [ 0 ] a^{[0]} a[0]。通过相似的衍生你会发现,后一层的表示同样可以写成类似的形式,得到 a [ 2 ] a^{[2]} a[2], y ^ = a [ 2 ] \hat{y} = a^{[2]} y^=a[2],具体过程见上述公式。
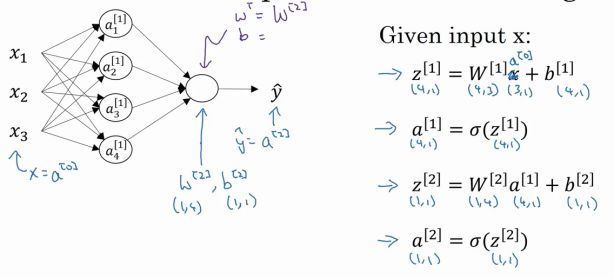
如上图左半部分所示为神经网络,把网络左边部分盖住先忽略,那么最后的输出单元就相当于一个逻辑回归的计算单元。当你有一个包含一层隐藏层的神经网络,你需要去实现以计算得到输出的是右边的四个等式,并且可以看成是一个向量化的计算过程,计算出隐藏层的四个逻辑回归单元和整个隐藏层的输出结果,如果编程实现需要的也只是这四行代码。
多样本向量化(Vectorizing across multiple examples)
逻辑回归是将各个训练样本组合成矩阵,对矩阵的各列进行计算。神经网络是通过对逻辑回归中的等式简单的变形,让神经网络计算出输出值。这种计算是所有的训练样本同时进行的,以下是实现它具体的步骤:
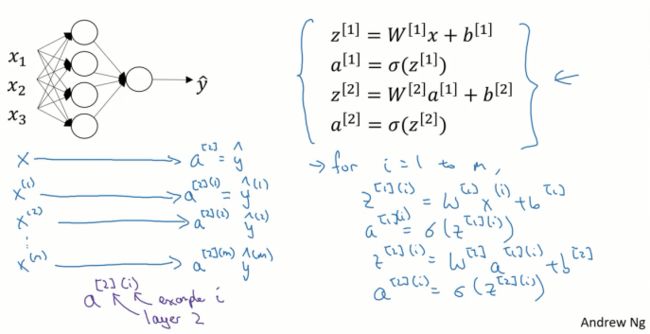
上文所述中得到的四个等式。它们给出如何计算出 z [ 1 ] z^{[1]} z[1], a [ 1 ] a^{[1]} a[1], z [ 2 ] z^{[2]} z[2], a [ 2 ] a^{[2]} a[2]。
对于一个给定的输入特征向量 X X X,这四个等式可以计算出 α [ 2 ] \alpha^{[2]} α[2]等于 y ^ \hat{y} y^。这是针对于单一的训练样本。如果有 m m m个训练样本,那么就需要重复这个过程。
用第一个训练样本 x [ 1 ] x^{[1]} x[1]来计算出预测值 y ^ [ 1 ] \hat{y}^{[1]} y^[1],就是第一个训练样本上得出的结果。
然后,用 x [ 2 ] x^{[2]} x[2]来计算出预测值 y ^ [ 2 ] \hat{y}^{[2]} y^[2],循环往复,直至用 x [ m ] x^{[m]} x[m]计算出 y ^ [ m ] \hat{y}^{[m]} y^[m]。
用激活函数表示法,如上图左下所示,它写成 a [ 2 ] ( 1 ) a^{[2](1)} a[2](1)、 a [ 2 ] ( 2 ) a^{[2](2)} a[2](2)和 a [ 2 ] ( m ) a^{[2](m)} a[2](m)。
【注】: a [ 2 ] ( i ) a^{[2](i)} a[2](i), ( i ) (i) (i)是指第 i i i个训练样本而 [ 2 ] [2] [2]是指第二层。
如果有一个非向量化形式的实现,而且要计算出它的预测值,对于所有训练样本,需要让 i i i从1到 m m m实现这四个等式:
z [ 1 ] ( i ) = W [ 1 ] ( i ) x ( i ) + b [ 1 ] ( i ) z^{[1](i)}=W^{[1](i)}x^{(i)}+b^{[1](i)} z[1](i)=W[1](i)x(i)+b[1](i)
a [ 1 ] ( i ) = σ ( z [ 1 ] ( i ) ) a^{[1](i)}=\sigma(z^{[1](i)}) a[1](i)=σ(z[1](i))
z [ 2 ] ( i ) = W [ 2 ] ( i ) a [ 1 ] ( i ) + b [ 2 ] ( i ) z^{[2](i)}=W^{[2](i)}a^{[1](i)}+b^{[2](i)} z[2](i)=W[2](i)a[1](i)+b[2](i)
a [ 2 ] ( i ) = σ ( z [ 2 ] ( i ) ) a^{[2](i)}=\sigma(z^{[2](i)}) a[2](i)=σ(z[2](i))
对于上面的这个方程中的 ( i ) ^{(i)} (i),是所有依赖于训练样本的变量,即将 ( i ) (i) (i)添加到 x x x, z z z和 a a a。如果想计算 m m m个训练样本上的所有输出,就应该向量化整个计算,以简化这列。
向量化实现:
x = [ ⋮ ⋮ ⋮ ⋮ x ( 1 ) x ( 2 ) ⋯ x ( m ) ⋮ ⋮ ⋮ ⋮ ] x = \left[ \begin{array}{c} \vdots & \vdots & \vdots & \vdots\\ x^{(1)} & x^{(2)} & \cdots & x^{(m)}\\ \vdots & \vdots & \vdots & \vdots\\ \end{array} \right] x=⎣⎢⎢⎡⋮x(1)⋮⋮x(2)⋮⋮⋯⋮⋮x(m)⋮⎦⎥⎥⎤
Z [ 1 ] = [ ⋮ ⋮ ⋮ ⋮ z [ 1 ] ( 1 ) z [ 1 ] ( 2 ) ⋯ z [ 1 ] ( m ) ⋮ ⋮ ⋮ ⋮ ] Z^{[1]} = \left[ \begin{array}{c} \vdots & \vdots & \vdots & \vdots\\ z^{[1](1)} & z^{[1](2)} & \cdots & z^{[1](m)}\\ \vdots & \vdots & \vdots & \vdots\\ \end{array} \right] Z[1]=⎣⎢⎢⎡⋮z[1](1)⋮⋮z[1](2)⋮⋮⋯⋮⋮z[1](m)⋮⎦⎥⎥⎤
A [ 1 ] = [ ⋮ ⋮ ⋮ ⋮ α [ 1 ] ( 1 ) α [ 1 ] ( 2 ) ⋯ α [ 1 ] ( m ) ⋮ ⋮ ⋮ ⋮ ] A^{[1]} = \left[ \begin{array}{c} \vdots & \vdots & \vdots & \vdots\\ \alpha^{[1](1)} & \alpha^{[1](2)} & \cdots & \alpha^{[1](m)}\\ \vdots & \vdots & \vdots & \vdots\\ \end{array} \right] A[1]=⎣⎢⎢⎡⋮α[1](1)⋮⋮α[1](2)⋮⋮⋯⋮⋮α[1](m)⋮⎦⎥⎥⎤
公式:
z [ 1 ] ( i ) = W [ 1 ] ( i ) x ( i ) + b [ 1 ] α [ 1 ] ( i ) = σ ( z [ 1 ] ( i ) ) z [ 2 ] ( i ) = W [ 2 ] ( i ) α [ 1 ] ( i ) + b [ 2 ] α [ 2 ] ( i ) = σ ( z [ 2 ] ( i ) ) } ⟹ { A [ 1 ] = σ ( z [ 1 ] ) z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] A [ 2 ] = σ ( z [ 2 ] ) \left. \begin{array}{r} \text{$z^{[1](i)} = W^{[1](i)}x^{(i)} + b^{[1]}$}\\ \text{$\alpha^{[1](i)} = \sigma(z^{[1](i)})$}\\ \text{$z^{[2](i)} = W^{[2](i)}\alpha^{[1](i)} + b^{[2]}$}\\ \text{$\alpha^{[2](i)} = \sigma(z^{[2](i)})$}\\ \end{array} \right\} \implies \begin{cases} \text{$A^{[1]} = \sigma(z^{[1]})$}\\ \text{$z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$}\\ \text{$A^{[2]} = \sigma(z^{[2]})$}\\ \end{cases} z[1](i)=W[1](i)x(i)+b[1]α[1](i)=σ(z[1](i))z[2](i)=W[2](i)α[1](i)+b[2]α[2](i)=σ(z[2](i))⎭⎪⎪⎬⎪⎪⎫⟹⎩⎪⎨⎪⎧A[1]=σ(z[1])z[2]=W[2]A[1]+b[2]A[2]=σ(z[2])
定义矩阵 X X X等于训练样本,将它们组合成矩阵的各列,形成一个 n n n维或 n n n乘以 m m m维矩阵。接下来计算见上述公式
以此类推,从小写的向量 x x x到这个大写的矩阵 X X X,只是通过组合 x x x向量在矩阵的各列中。
同理, z [ 1 ] ( 1 ) z^{[1](1)} z[1](1), z [ 1 ] ( 2 ) z^{[1](2)} z[1](2)等等都是 z [ 1 ] ( m ) z^{[1](m)} z[1](m)的列向量,将所有 m m m都组合在各列中,就的到矩阵 Z [ 1 ] Z^{[1]} Z[1]。
同理, a [ 1 ] ( 1 ) a^{[1](1)} a[1](1), a [ 1 ] ( 2 ) a^{[1](2)} a[1](2),……, a [ 1 ] ( m ) a^{[1](m)} a[1](m)将其组合在矩阵各列中,如同从向量 x x x到矩阵 X X X,以及从向量 z z z到矩阵 Z Z Z一样,就能得到矩阵 A [ 1 ] A^{[1]} A[1]。
同样的,对于 Z [ 2 ] Z^{[2]} Z[2]和 A [ 2 ] A^{[2]} A[2],也是这样得到。
这种符号其中一个作用就是,可以通过训练样本来进行索引。这就是水平索引对应于不同的训练样本的原因,这些训练样本是从左到右扫描训练集而得到的。
在垂直方向,这个垂直索引对应于神经网络中的不同节点。例如,这个节点,该值位于矩阵的最左上角对应于激活单元,它是位于第一个训练样本上的第一个隐藏单元。它的下一个值对应于第二个隐藏单元的激活值。它是位于第一个训练样本上的,以及第一个训练示例中第三个隐藏单元,等等。
当垂直扫描,是索引到隐藏单位的数字。当水平扫描,将从第一个训练示例中从第一个隐藏的单元到第二个训练样本,第三个训练样本……直到节点对应于第一个隐藏单元的激活值,且这个隐藏单元是位于这 m m m个训练样本中的最终训练样本。
从水平上看,矩阵 A A A代表了各个训练样本。从竖直上看,矩阵 A A A的不同的索引对应于不同的隐藏单元。
对于矩阵 Z , X Z,X Z,X情况也类似,水平方向上,对应于不同的训练样本;竖直方向上,对应不同的输入特征,而这就是神经网络输入层中各个节点。
神经网络上通过在多样本情况下的向量化来使用这些等式。
向量化实现的解释(Justification for vectorized implementation)
在上文第二节中,我们学习到如何将多个训练样本横向堆叠成一个矩阵 X X X,然后就可以推导出神经网络中前向传播(forward propagation)部分的向量化实现。
在这里解释一下,为什么上一节中写下的公式就是将多个样本向量化的正确实现。
我们先手动对几个样本计算一下前向传播,看看有什么规律:
公式:
z [ 1 ] ( 1 ) = W [ 1 ] x ( 1 ) + b [ 1 ] z^{[1](1)} = W^{[1]}x^{(1)} + b^{[1]} z[1](1)=W[1]x(1)+b[1]
z [ 1 ] ( 2 ) = W [ 1 ] x ( 2 ) + b [ 1 ] z^{[1](2)} = W^{[1]}x^{(2)} + b^{[1]} z[1](2)=W[1]x(2)+b[1]
z [ 1 ] ( 3 ) = W [ 1 ] x ( 3 ) + b [ 1 ] z^{[1](3)} = W^{[1]}x^{(3)} + b^{[1]} z[1](3)=W[1]x(3)+b[1]
这里,为了描述的简便,我们先忽略掉 b [ 1 ] b^{[1]} b[1]后面你将会看到利用Python 的广播机制,可以很容易的将 b [ 1 ] b^{[1]} b[1] 加进来。
现在 W [ 1 ] W^{[1]} W[1] 是一个矩阵, x ( 1 ) , x ( 2 ) , x ( 3 ) x^{(1)},x^{(2)},x^{(3)} x(1),x(2),x(3)都是列向量,矩阵乘以列向量得到列向量,下面将它们用图形直观的表示出来:
公式:
W [ 1 ] x = [ ⋯ ⋯ ⋯ ] [ ⋮ ⋮ ⋮ ⋮ x ( 1 ) x ( 2 ) x ( 3 ) ⋮ ⋮ ⋮ ⋮ ⋮ ] = [ ⋮ ⋮ ⋮ ⋮ w ( 1 ) x ( 1 ) w ( 1 ) x ( 2 ) w ( 1 ) x ( 3 ) ⋮ ⋮ ⋮ ⋮ ⋮ ] = [ ⋮ ⋮ ⋮ ⋮ z [ 1 ] ( 1 ) z [ 1 ] ( 2 ) z [ 1 ] ( 3 ) ⋮ ⋮ ⋮ ⋮ ⋮ ] = Z [ 1 ] W^{[1]} x = \left[ \begin{array}{ccc} \cdots \\ \cdots \\ \cdots \\ \end{array} \right] \left[ \begin{array}{c} \vdots &\vdots & \vdots & \vdots \\ x^{(1)} & x^{(2)} & x^{(3)} & \vdots\\ \vdots &\vdots & \vdots & \vdots \\ \end{array} \right] = \left[ \begin{array}{c} \vdots &\vdots & \vdots & \vdots \\ w^{(1)}x^{(1)} & w^{(1)}x^{(2)} & w^{(1)}x^{(3)} & \vdots\\ \vdots &\vdots & \vdots & \vdots \\ \end{array} \right] =\\ \left[ \begin{array}{c} \vdots &\vdots & \vdots & \vdots \\ z^{[1](1)} & z^{[1](2)} & z^{[1](3)} & \vdots\\ \vdots &\vdots & \vdots & \vdots \\ \end{array} \right] = Z^{[1]} W[1]x=⎣⎡⋯⋯⋯⎦⎤⎣⎢⎢⎢⎡⋮x(1)⋮⋮x(2)⋮⋮x(3)⋮⋮⋮⋮⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡⋮w(1)x(1)⋮⋮w(1)x(2)⋮⋮w(1)x(3)⋮⋮⋮⋮⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡⋮z[1](1)⋮⋮z[1](2)⋮⋮z[1](3)⋮⋮⋮⋮⎦⎥⎥⎥⎤=Z[1]
从图中可以看出,当加入更多样本时,只需向矩阵 X X X中加入更多列。
所以从这里我们也可以了解到,为什么之前我们对单个样本的计算要写成
z [ 1 ] ( i ) = W [ 1 ] x ( i ) + b [ 1 ] z^{[1](i)} = W^{[1]}x^{(i)} + b^{[1]} z[1](i)=W[1]x(i)+b[1]
这种形式,因为当有不同的训练样本时,将它们堆到矩阵 X X X的各列中,那么它们的输出也就会相应的堆叠到矩阵 Z [ 1 ] Z^{[1]} Z[1] 的各列中。现在我们就可以直接计算矩阵 Z [ 1 ] Z^{[1]} Z[1] 加上 b [ 1 ] b^{[1]} b[1],因为列向量 b [ 1 ] b^{[1]} b[1] 和矩阵 Z [ 1 ] Z^{[1]} Z[1]的列向量有着相同的尺寸,而Python的广播机制对于这种矩阵与向量直接相加的处理方式是,将向量与矩阵的每一列相加。
所以这里只是说明了为什么公式 Z [ 1 ] = W [ 1 ] X + b [ 1 ] Z^{[1]} =W^{[1]}X + \ b^{[1]} Z[1]=W[1]X+ b[1]是前向传播的第一步计算的正确向量化实现,但事实证明,类似的分析可以发现,前向传播的其它步也可以使用非常相似的逻辑,即如果将输入按列向量横向堆叠进矩阵,那么通过公式计算之后,也能得到成列堆叠的输出。