Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution——论文笔记
目录
- 1. Motivation
- 2. 相关工作
- 2.1 提高CNN框架的效率
- 2.2 多尺度表示学习
- 3 网络结构
- 3.1 Octave特征表示
- 3.2 Octave 卷积
- 3.3实现细节
- 4 实验
- 4.1 实验设置
- 4.2 模型简化测试
- 4.3 和当前在ImageNet上SOTAs相比
- 5 总结
论文传送门:
Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
1. Motivation
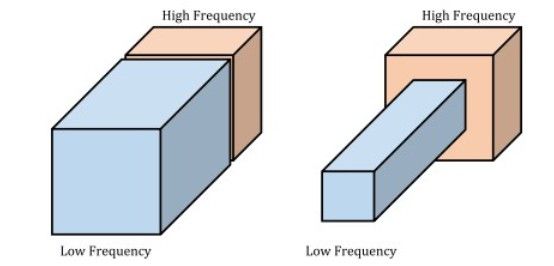
声音频段中有高频部分和低频部分,图片像素中也可以将信息分为高频信息和低频信息,低频信息中包含那些缓慢变化的、结构性的信息,而高频信息一般包含那些变化较大、包含图片细节的信息,因此我们可以把一张图片认为是高频信息和低频信息的混合表示。下图是一个图像的高频信息和低频信息分离表示。

为了提高CNN的性能和准确率,有很多的工作致力于减少模型参数内在的冗余,在加快训练速度的同时能够获得更多正交的高级特征从而提高模型的表示能力,但是实际上每一层CNN输出的特征图也存在着大量的冗余,我们以原始输入为例,图片的每一个像素之间并不是孤立的,相邻的元素之间存在着密切的联系,将它们联合在一起存储表示往往能够更加准确的描述图片的信息,所以我们以单一像素的形式存储是及其浪费存储和计算资源的。
因此,我们可以将特征图按照频率分成两部分,一部分是高频信息,一部分是低频信息,然后我们可以将低频信息的数据通过使相邻元素之间共享信息来降维,进而降低其空间冗余性。在对低维数据进行处理的时候,我们还相当于变相的扩大了其感受野,使得网络能够学习到更加高级的特征,有助于提高网络的准确性。
本文的贡献如下:
- 提出将卷积特征图按照不同的频率分成两组,并对不同频率的数据进行不同的卷积处理。因为低频信息可以被安全的压缩而不用担心影响网络的准确率,所以这可以使得我们节省大量的存储和计算资源;
- 设计了一个名为OctConv的即插即用的运行单元,可以直接作为普通CNN卷积运算单元的替换,OctConv可以直接处理我们提出的新的特征图表示并且降低了低频数据的冗余性;
- 使用上面设计的OctConv实现流行的CNN框架,并与当前最好结果进行对比,同时和当前最好的AutoML框架进行了对比。
2. 相关工作
2.1 提高CNN框架的效率
自从AlexNet、VGG等框架使用堆叠大量卷积层的方法构架网络并取得了巨大的成绩之后,研究者们为了提高CNN的效率做出了很多的努力。
ResNet、DenseNet通过增加跨越多层的快捷连接来加强特征的重用,同时也是为了减轻梯度消失问题,降低了优化的困难。如下图所示:
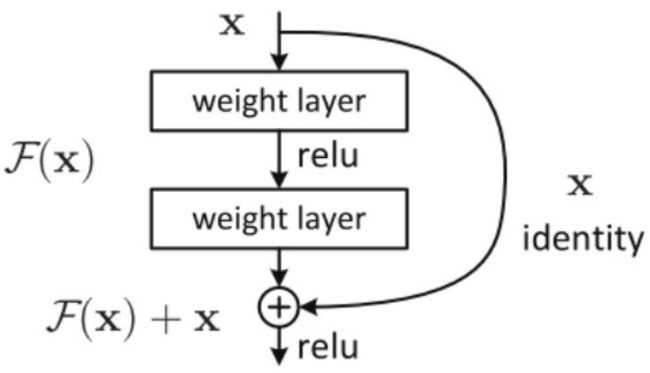
因为我们可以在现有网络结构上直接堆叠一个恒等映射层,也就是一个什么都不做的层,而不影响整体的效果,所以深层网络不应该比稍浅一些的网络造成更大的误差,所以ResNet引入了残差块,并且希望该结构能够fit剩余映射,而不是直接去fit底层映射。ResNet并不是第一个利用快捷连接的神经网络,Highway Network首次引入了Gated shortcut connections,用于控制通过该连接的信息量,同样的思想我们还可以在LSTM的设计中发现,它利用不同的门控单元来控制信息的流动。
ResNeXt和ShuffleNet框架利用稀疏连接的分组卷积方法来降低不同通道之间的冗余性,如下图所示:
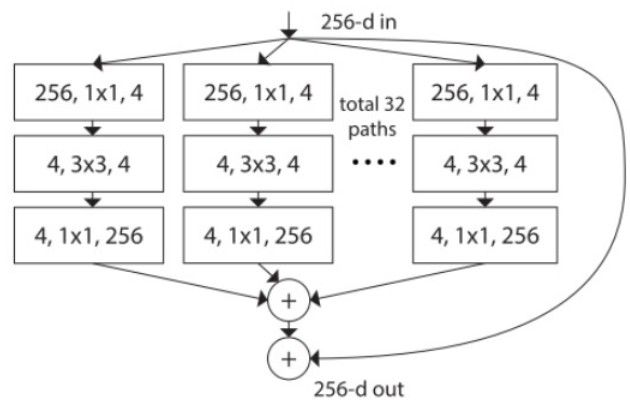
Xception和MobileNet使用深度可分离卷积层来减小连接的密集程度。
2.2 多尺度表示学习
本文提出的OctConv在不同的空间分辨率下对特征图进行卷积,得到了具有较大接收域的多尺度特征表示。尺度空间很早就被用于局部特征提取,比如之前很流行的SIFT特征,在深度学习领域,现有方法主要聚焦于融合多尺度特征,更好的获取全局信息。然而类似的这些方法大多只在网络结构的某些曾或者网络的末端加入提出的新的结构,bL-Net和ELASTIC-Net使用频繁的对特征图进行上采样和下采样来捕获多尺度特征。但是以上这些方法都是设计为残差块的替代品,当被用于不同的网络结构时需要额外的专业知识和更多的超参数优化。
3 网络结构
3.1 Octave特征表示
对于一般的CNN来说,输入和输出特征图的空间分辨率是相同的,然而对于空间频率模型,即本文提出的方法来说,一个自然图片可以被因式分解成捕获全局信息和粗略架构的低频信号和捕获优化细节的高频信号。我们认为存在一个特征图的子集可以表示空间中的低频信号的变化和冗余信息。
为了减少这种空间冗余性,我们引入了Octave特征表示,显示的将特征图分成了高频和低频两部分。假设输入特征图为 X ∈ R c ∗ h ∗ w X \in R^{c*h*w} X∈Rc∗h∗w,其中c是通道数,h、w是特征图的尺寸,我们在通道维度将特征图分为两部分,即 X = { X H , X L } X=\{X^H, X^L\} X={XH,XL},其中, X H ∈ R ( 1 − α ) c ∗ h ∗ w , X L ∈ R α c ∗ h 2 ∗ w 2 , α ∈ { 0 , 1 } X^H \in R^{(1-\alpha)c*h*w},X^L \in R^{\alpha c * \frac{h} {2}* \frac{w}{2}}, \ \ \alpha \in \{0,1\} XH∈R(1−α)c∗h∗w,XL∈Rαc∗2h∗2w, α∈{0,1}, α \alpha α表示通道被分配到低频部分的比例。如下图所示:
3.2 Octave 卷积
上面介绍的Octave特征表示降低了低频信息的空间冗余性,并且比正常CNN特征表示更加复杂,所以不能直接被正常的CNN所处理,一直比较Naive的做法是对低频表示进行上采样使其达到和高频信息一致的尺寸然后组合这两个部分,就可以得到能够被普通CNN处理的数据格式,但是这种做法即增加了内存的消耗,也增加了大量的计算。因此,本文设计了可以直接处理 X = { X H , X L } X=\{X^H, X^L\} X={XH,XL}这种特征表示的卷积层:Octave Convolution。
Vanilla Convolution:
设 W ∈ R c ∗ k ∗ k W \in R^{c*k*k} W∈Rc∗k∗k表示一个卷积核, X , Y ∈ R c ∗ h ∗ w X,Y \in R^{c*h*w} X,Y∈Rc∗h∗w表示输入和输出张量,那么输出特征 Y p , q ∈ R c Y_{p,q} \in R^c Yp,q∈Rc可以表示为:
Y p , q = ∑ i , j ∈ N k W ( i + k − 1 2 , j + k − 1 2 ) T X ( p + i , q + j ) Y_{p,q}=\sum_{i, j \in N_k} W_{(i + \frac{k-1}{2}, j + \frac{k-1}{2})}^T X_{(p+i, q+j)} Yp,q=i,j∈Nk∑W(i+2k−1,j+2k−1)TX(p+i,q+j)
上式比较简单,这里不多做解释。
Octave Convolution:
我们的目标是在分别对高频和低频信息进行卷积处理的同时还允许二者之间进行有效的信息交互。因此由上面的介绍我们可以得到:
Y H = Y H → H + Y L → H Y L = Y L → L + Y H → L Y^H=Y^{H\rightarrow H} + Y^{L \rightarrow H}\\ Y^L=Y^{L\rightarrow L} + Y^{H \rightarrow L}\\ YH=YH→H+YL→HYL=YL→L+YH→L
如下图所示:
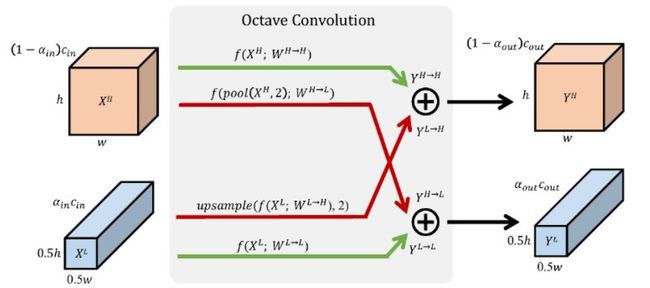
为了上面的计算,我们将卷积核W分成四个部分 W = { W H , W L } = { W H → H , W H → L , W L → L , W L → H } W=\{W^H, W^L\}=\{W^{H\rightarrow H}, W^{H\rightarrow L}, W^{L\rightarrow L}, W^{L\rightarrow H}\} W={WH,WL}={WH→H,WH→L,WL→L,WL→H},如下图所示:
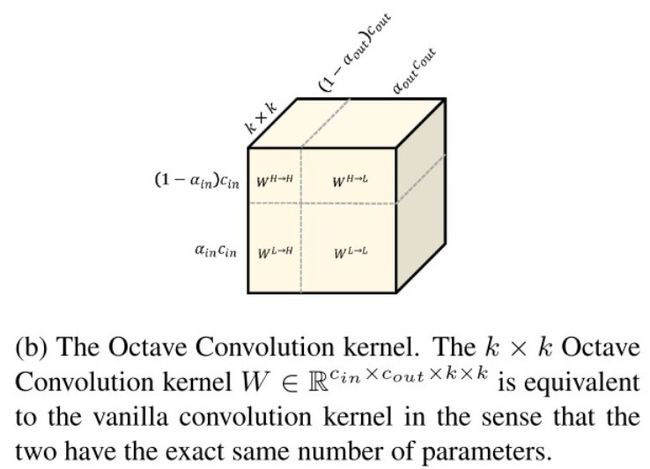
对于频内信息交流,我们直接使用普通的CNN卷积计算,对于频间的信息交流,我们将上/下采样和卷积操作放在一起,避免了显示的计算和存储采样结果。公式如下:
Y p , q H = Y p , q H → H + Y p , q L → H = ∑ i , j ∈ N k W i + k − 1 2 , j + k − 1 2 H → H T X p + i , q + j H + ∑ i , j ∈ N k W i + k − 1 2 , j + k − 1 2 L → H T X ⌊ p 2 ⌋ + i , ⌊ q 2 ⌋ + j L \begin{aligned} Y_{p,q}^H&=Y_{p,q}^{H\rightarrow H} + Y_{p, q}^{L\rightarrow H}\\ &=\sum_{i,j \in N_k}{W_{i+\frac{k-1}{2}, j +\frac{k-1}{2}}^{H\rightarrow H}}^T X_{p+i, q+j}^H\\ &+\sum_{i,j \in N_k}{W_{i+\frac{k-1}{2}, j +\frac{k-1}{2}}^{L\rightarrow H}}^TX_{\lfloor \frac{p}{2} \rfloor +i, \lfloor \frac{q}{2} \rfloor+j}^L \end{aligned} Yp,qH=Yp,qH→H+Yp,qL→H=i,j∈Nk∑Wi+2k−1,j+2k−1H→HTXp+i,q+jH+i,j∈Nk∑Wi+2k−1,j+2k−1L→HTX⌊2p⌋+i,⌊2q⌋+jL
Y p , q L = Y p , q L → L + Y p , q H → L = ∑ i , j ∈ N k W i + k − 1 2 , j + k − 1 2 L → L T X p + i , q + j L + ∑ i , j ∈ N k W i + k − 1 2 , j + k − 1 2 H → L T X 2 ∗ p + 0.5 + i , 2 ∗ q + 0.5 + j H \begin{aligned} Y_{p,q}^L&=Y_{p,q}^{L\rightarrow L} + Y_{p, q}^{H\rightarrow L}\\ &=\sum_{i,j \in N_k}{W_{i+\frac{k-1}{2}, j +\frac{k-1}{2}}^{L\rightarrow L}}^T X_{p+i, q+j}^L\\ &+\sum_{i,j \in N_k}{W_{i+\frac{k-1}{2}, j +\frac{k-1}{2}}^{H\rightarrow L}}^TX_{2*p+0.5+i, 2*q+0.5+j}^H \end{aligned} Yp,qL=Yp,qL→L+Yp,qH→L=i,j∈Nk∑Wi+2k−1,j+2k−1L→LTXp+i,q+jL+i,j∈Nk∑Wi+2k−1,j+2k−1H→LTX2∗p+0.5+i,2∗q+0.5+jH
上式中的 ⌊ p 2 ⌋ \lfloor \frac{p}{2} \rfloor ⌊2p⌋是为了上采样,同样的, 2 ∗ p + 0.5 + i 2*p+0.5+i 2∗p+0.5+i的目的是下采样,加上0.5度目的是为了保证下采样之后的输出特征图分布不偏移,相当于平均池化。
通过设置不同的 α \alpha α值,我们可以将数据进行不同程度的压缩,同时节省了大量的计算,下面是一个统计表:
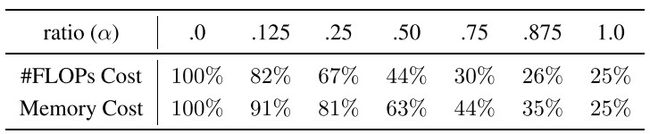
3.3实现细节
上一节中我们提到下采样时使用平均池化的思想,而不是一般的Strided convolution,具体原因如下图:
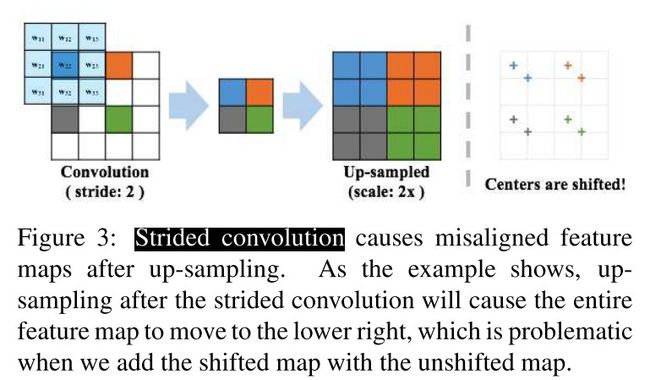
如文中所述,使用Strided convolution会导致输出的特征图偏移。
这样,我们可以将Octave Convolution的计算表示如下:
Y H = f ( X H ; W H → H ) + upsample ( f ( X L ; W L → H ) , 2 ) Y L = f ( X L ; W L → L ) + f ( pool ( X H , 2 ) ; W H → L ) ) \begin{aligned} Y^{H} &=f\left(X^{H} ; W^{H \rightarrow H}\right)+\text { upsample }\left(f\left(X^{L} ; W^{L \rightarrow H}\right), 2\right) \\ Y^{L} &=f\left(X^{L} ; W^{L \rightarrow L}\right)+f\left(\operatorname{pool}\left(X^{H}, 2\right) ; W^{H \rightarrow L}\right) ) \end{aligned} YHYL=f(XH;WH→H)+ upsample (f(XL;WL→H),2)=f(XL;WL→L)+f(pool(XH,2);WH→L))
Octave Convolution还适用于一些常见变种卷积类型,比Group Convoolution和Depthwise Conolution。这里多介绍一下这两种卷积的工作方式:
Group Convoolution:分组卷积最早在AlexNet中出现,由于当时的硬件资源有限,训练AlexNet时卷积操作不能全部放在同一个GPU处理,因此作者把feature maps分给多个GPU分别进行处理,最后把多个GPU的结果进行融合。
具体来说就是对于输入 X ∈ R c 1 ∗ h ∗ w X \in \mathcal{R}^{c_1*h*w} X∈Rc1∗h∗w,普通卷积方式是用 c 2 c_2 c2个大小为 c 1 ∗ k ∗ k c_1*k*k c1∗k∗k的卷积核对输入进行卷积计算,其中 c 2 c_2 c2是输出通道数, c 1 c_1 c1是输入通道数,h,w是输入特征图大小, k ∗ k k*k k∗k是卷积核大小,当输入规模很大时,这个计算需要很大的存储,因此我们可以将它分成两部分来计算,我们将输入和输出在通道那个维度切分成两个部分,将输入数据分成了2组(组数为g),需要注意的是,这种分组只是在深度上进行划分,即某几个通道编为一组,这个具体的数量由 c 1 / g c_1/g c1/g决定。因为输出数据的改变,相应的,卷积核也需要做出同样的改变。即每组中卷积核的深度也就变成了 c 1 / g c_1/g c1/g,而卷积核的大小是不需要改变的,此时每组的卷积核的个数就变成了 c 2 / g c_2/g c2/g个,而不是原来的 c 2 c_2 c2了。然后用每组的卷积核同它们对应组内的输入数据卷积,得到了输出数据以后,再用concatenate的方式组合起来,最终的输出数据的通道仍旧是 c 2 c_2 c2。
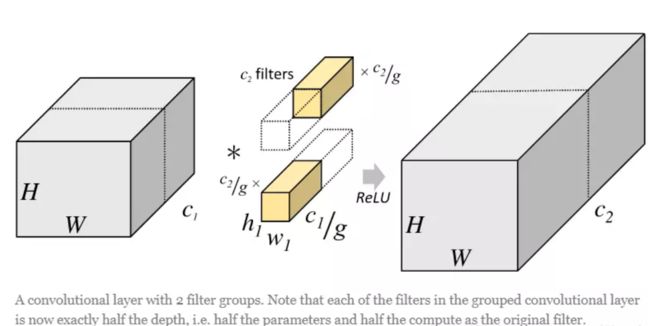
我们可以看到分组卷积减少了大量的计算,但是同时由于直接简单的将输入按照通道分成了多个组,而多个组之间没有任何的信息交流,所以对特征的捕获是不利的。
Depthwise Conolution:Depthwise(DW)卷积与Pointwise(PW)卷积,合起来被称作Depthwise Separable Convolution(参见Google的Xception),该结构和常规卷积操作类似,可用来提取特征,但相比于常规卷积操作,其参数量和运算成本较低。所以在一些轻量级网络中会碰到这种结构如MobileNet。
不同于常规卷积操作,Depthwise Convolution的一个卷积核负责一个通道,一个通道只被一个卷积核卷积。上面所提到的常规卷积每个卷积核是同时操作输入图片的每个通道。同样是对于一张5×5像素、三通道彩色输入图片(shape为5×5×3),Depthwise Convolution首先经过第一次卷积运算,不同于上面的常规卷积,DW完全是在二维平面内进行。卷积核的数量与上一层的通道数相同(通道和卷积核一一对应)。所以一个三通道的图像经过运算后生成了3个Feature map(如果有same padding则尺寸与输入层相同为5×5),如下图所示:

Depthwise Convolution完成后的Feature map数量与输入层的通道数相同,无法扩展Feature map。而且这种运算对输入层的每个通道独立进行卷积运算,没有有效的利用不同通道在相同空间位置上的feature信息。因此需要Pointwise Convolution来将这些Feature map进行组合生成新的Feature map。
Pointwise Convolution的运算与常规卷积运算非常相似,它的卷积核的尺寸为 1×1×M,M为上一层的通道数。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合,生成新的Feature map。有几个卷积核就有几个输出Feature map。如下图所示。

对于Group Convolution,我们看可以简单的把Octave Convolution的四个卷积操作都替换成Group Convolution,同样的,对于Depthwise Convolution也可以这样做。
4 实验
4.1 实验设置
选取了一些比较流行的CNN框架,并将它们的出了第一层卷积层之外的卷积层替换为Octave Convolution,并增加了一个超参数 α \alpha α,表示低频信息的比例。
4.2 模型简化测试
探究了两个问题:
- OctConv是否比普通CNN能够更好的权衡算力和准确率?
- OctConv适合在什么样的情形下使用?
在几个流行框架上的测试结果如下图所示:

观察结果如下:
- flops-accuracy权衡曲线为凹曲线,精度先上升后缓慢下降。
- 我们主要观察到两个特殊的点:第一个在α= 0.5,网络得到类似或者更好的结果;第二个在α= 0.125,网络达到最好的精度,比baseline高出1.2%。
我们将准确度的提高归功于OctConv对高低频信息处理的有效设计以及相应的扩大低频信息的感受野,它提供了更多的上下文信息。准确率达在到最高点之后并没有突然下降,表明对低频信息的高度压缩不会导致重大的信息丢失。有趣的是,75%的feature map可以压缩到一半的分辨率,而准确率只有0.4%的下降,这证明了对平滑变化的feature map进行分组和压缩的有效性,可以减少CNNs中的空间冗余。
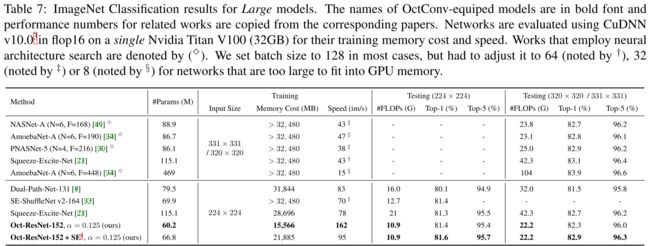
4.3 和当前在ImageNet上SOTAs相比
见下图:
5 总结
本文所做的工作主要解决了普通CNN中feature map中的信息冗余问题,并提出了OctConv,其可以非常方便的用于其他比较流行的CNN架构,在节省了大量的计算和存储资源的同时,通过不同频率之间的信息交换和感受野的夸大,对模型的精度有些许的提高。