受限玻尔兹曼机(RBM)+对比散度算法(CD-k)
受限玻尔兹曼机(RBM)+对比散度算法(CD-k)
- 主要内容：
- 受限玻尔兹曼机（RBM）基本原理
- 受限玻尔兹曼机（RBM）训练过程——对比散度算法（CD-k）
1. 受限玻尔兹曼机（RBM）基本原理
受限玻尔兹曼机(RBM)是一种典型的神经网络模型，由一层可视层 v 和一层隐藏层 h 组成，该网络的可视层 v 和隐藏层 h 神经元彼此互联，但同一层内神经元无连接，如图1。RBM能够通过隐藏层获得可视层神经元的高阶相关性，因此可以通过RBM进行特征提取。RBM中神经元有两种状态:“激活”和“未激活”，一般用二进制的1和0表示。受限玻尔兹曼机一个最主要的优点是在给定可视层神经元状态时，隐藏层某一神经元的状态是条件独立于该隐藏层其它神经元的状态；反之，各个可视层神经元的状态亦条件独立。
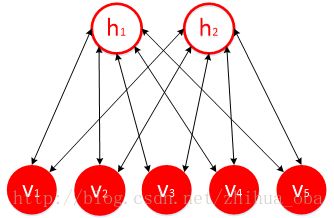
图1 RBM模型
受限玻尔兹曼机是一种基于能量的模型，可视层神经元向量 v 和隐藏层神经元向量 h 联合配置的能量函数为：
(1−1)
联合似然为：
(1−2)
条件似然函数为：
(1−3)
隐藏层各神经元的条件概率为：
(1−4)
可视层各神经元的条件概率为：
(1−5)
，为
sigmoid 激活函数。
若 b ， c ， W 均为训练好的参数。对于样本集中任意一个样本点 xi=(xi,1,xi,2,...,xi,n) (n为属性个数)，其属性值 xi,j 对应可视层神经元 vj 。根据公式(1-4)，将样本点 xi 所有属性值代入公式(1-4)，可得特征提取后的样本点 x′i 。
接下来介绍如何对RBM进行训练得到参数 b ， c ， W 。
2. 受限玻尔兹曼机（RBM）训练过程——对比散度算法（CD-k）
学习RBM的任务是求出参数的值，来拟合给定的训练数据。Hinton[1]提出了RBM的一个快速学习算法，即对比散度(Contrastive Divergence，CD)。由于CD-k算法中（k表示采样次数），当k=1时，即只进行一步吉布斯采样，就能达到很好的拟合效果[2]。故一般采用CD-1算法的形式，来拟合各参数的值，如图2。
图2 CD-1
设可视层 v 的重构（reconstruction）为 v∗ ，根据重构的可视层 v∗ 所得隐藏层为 h∗ 。设学习效率为 ε ，经过对比散度算法对RBM进行训练后，权重矩阵 W 、可视层的偏置向量 b 、隐藏层的偏置向量 c ，根据文献[1][3]，更新规则如下：
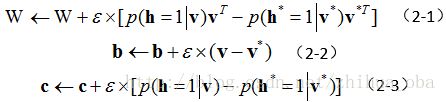
RBM的对比散度算法主要步骤：根据训练集中样本点设置可视层神经元 v 激活状态，根据公式（1-4）计算所有隐藏层神经元状态；在隐藏层各神经元的状态 h 确定之后，根据公式（1-5）计算在隐藏层确定的情况下，所有可视层神经元的状态，从而产生可视层的一个重构 v∗ ；如果此时 v 和 v∗ 一样，那么得到的隐藏层 h 就是可视层 v 的另外一种表达，此时隐藏层可以作为可视层输入数据的特征。同时在训练中，可以利用可视层的状态与重构可视层的状态的误差来调整RBM的参数，从而使得 v 和 v∗ 的重构误差尽可能减小。
对于初学者来讲，在训练RBM的过程中，并不了解如何根据样本点 xi=(xi,1,xi,2,...,xi,n) (n为属性个数)来设置对应可视层 v 的状态，以及如何设置隐藏层神经元的状态。此处提供一种常用的方法，并做简要说明：
对于训练集 S 中所有样本点 (x1,x2,...,xN) （N为训练样本点的个数），计算在第 j 个属性下所有样本点的最大值 maxi∈N(xi,j) ，以及最小值 mini∈N(xi,j) ，当 xi,j−mini∈N(xi,j)maxi∈N(xi,j)−mini∈N(xi,j) 大于阈值 δj,1 时，则对应可视层神经元状态处于激活状态，即“1”，否则为“0”。将可视层神经元状态值，此时只有“0”和“1”，代入至公式（1-4），得到隐藏层神经元的激活概率，当激活概率大于阈值 δj,2 时，隐藏层神经元的状态值为“1”，否则为“0”。阈值 δj,1 ， δj,2 的设定，可以根据数据集的不同有所不同，亦或是随机产生[0,1]上的随机数，作为 δj,1 ， δj,2 的值。
关于对比散度算法中，相关参数的设置，文献[3]给出了一些初步的方法，感兴趣的小童鞋，可以了解一下。
- 参考文献：
[1] Hinton G E. Training products of experts by minimizing contrastive divergence[J]. Neural Computation, 2002, 14(8):1771-1800.
[2] Bengio Y. Learning Deep Architectures for AI[J]. Foundations & Trends® in Machine Learning, 2009, 2(1):1-127.
[3] 张春霞, 姬楠楠, 王冠伟. 受限波尔兹曼机?[J]. 工程数学学报, 2015(2):159-173.