MLE估计和MAP估计 —— 基础解析与实例
0. 开头
最近在学习机器学习的过程中,了解到了三种参数估计方法,最大似然估计(Maximum Likelihood Estimation)、最大后验概率估计(Maximum A Posterior Estimation)和贝叶斯估计(Bayesian Estimation)。MLE估计较为基础,大多数本科阶段数理统计课程都会有所涉及,故一笔略过;本文重点介绍后两类参数估计方法,并逐一给出示例。
1. MLE估计
MLE估计的假设条件是随机变量独立同分布,因此若我们知道随机变量总体的分布(概率密度函数),其样本点的联合概率密度函数可写作:
f ( x 1 , x 2 , x 3 , . . . . . . , x n , Θ ) = f ( x 1 , Θ ) ∗ f ( x 2 , Θ ) ∗ f ( x 3 , Θ ) ∗ . . . . . . ∗ f ( x n , Θ ) f(x_1,x_2,x_3,......,x_n,\Theta) = f(x_1,\Theta)*f(x_2,\Theta)*f(x_3,\Theta)*......*f(x_n,\Theta) f(x1,x2,x3,......,xn,Θ)=f(x1,Θ)∗f(x2,Θ)∗f(x3,Θ)∗......∗f(xn,Θ)
其核心思想就是求解未知参数使得当前样本发生的概率最大,用数学表达式写出来就是(此处默认只有一个参数):
Θ ^ M L = a r g m a x f ( x 1 , x 2 , . . . , x n ∣ Θ ) \hat{\Theta}_{ML} = argmax f(x_1,x_2,...,x_n|\Theta) Θ^ML=argmaxf(x1,x2,...,xn∣Θ)
1.1 MLE估计实例
抛硬币十次,结果6正4反。假设如果正面朝上,随机变量X取1,反之取0,故我们得到一组样本
{1,1,1,1,1,1,0,0,0,0}。很明显X符合伯努利分布,其概率密度函数(pdf)为:
f x = Θ x ( 1 − Θ ) ( 1 − x ) f_x={\Theta}^x(1-{\Theta})^{(1-x)} fx=Θx(1−Θ)(1−x)
从常识来说,我们都知道投掷一枚正常的硬币,得到正面的概率为0.5,但是现在假设我们并不知道参数的总体分布,仅依据十个样本点推断概率的总体估计。因为X是独立同分布的,我们写出10次试验的联合概率密度函数:
f ( x 1 , x 2 , x 3 , . . . . . . , x 10 , Θ ) = Θ 6 ( 1 − Θ ) 4 f(x_1,x_2,x_3,......,x_{10},\Theta) =\Theta^{6}(1-\Theta)^{4} f(x1,x2,x3,......,x10,Θ)=Θ6(1−Θ)4
为方便计算,两边取log:
l n f ( x 1 , x 2 , x 3 , . . . . . . , x 10 , Θ ) = 6 l n Θ + 4 l n ( 1 − Θ ) lnf(x_1,x_2,x_3,......,x_{10},\Theta) =6ln\Theta+4ln(1-\Theta) lnf(x1,x2,x3,......,x10,Θ)=6lnΘ+4ln(1−Θ)
对θ求导:
∂ l n f ( x 1 , x 2 , x 3 , . . . . . . , x 10 , Θ ) ∂ Θ = 0 \frac{\partial lnf(x_1,x_2,x_3,......,x_{10},\Theta)}{\partial \Theta} =0 ∂Θ∂lnf(x1,x2,x3,......,x10,Θ)=0
最终得到:
Θ ^ M L = 6 / 10 \hat{\Theta}_{ML} = 6/10 Θ^ML=6/10
这个例子可以看到,最大似然估计量就是实验中正面出现的频率。Intuitively,只有出现正面概率是0.6的时候,抛十次硬币得到6正4反的概率才最大化。由于MLE是根据样本子集对总体分布情况进行估计,在样本子集数据量较少时,并不是特别准确。如果实验次数变为100、1000次,MLE估计量会逐渐逼近0.5。
2. MAP估计
在MLE估计的情况下,我们对未知参数的分布一无所知。而在MAP估计的情景下,我们对未知参数会有一个先验的分布认知,例如在上一个抛硬币例子中,我们事前清楚正面朝上的概率是50%。在此基础上,我们通过样本数据对先验概率进行“调节”,最终得到一个最大化的参数估计。数学表达式为:
P ( Θ ∣ x 1 , x 2 , . . . , x n ) = P ( x 1 , x 2 , . . . , x n ∣ Θ ) P ( Θ ) P ( x 1 , x 2 , . . . , x n ) P(\Theta |x_1,x_2,...,x_n) = \frac{P(x_1,x_2,...,x_n|\Theta)P(\Theta)}{P(x_1,x_2,...,x_n)} P(Θ∣x1,x2,...,xn)=P(x1,x2,...,xn)P(x1,x2,...,xn∣Θ)P(Θ)
上述公式中,P (Θ)就是参数的先验概率分布,P(x1,x2,…,xn|Θ)是样本的联合分布函数。我们的目标是:
Θ ^ M A P = A r g m a x P ( x 1 , x 2 , . . . , x n ∣ Θ ) P ( Θ ) P ( x 1 , x 2 , . . . , x n ) \hat{\Theta}_{MAP} = Argmax \frac{P(x_1,x_2,...,x_n|\Theta)P(\Theta)}{P(x_1,x_2,...,x_n)} Θ^MAP=ArgmaxP(x1,x2,...,xn)P(x1,x2,...,xn∣Θ)P(Θ)
由于分母是常数,故:
Θ ^ M A P = A r g m a x P ( x 1 , x 2 , . . . , x n ∣ Θ ) P ( Θ ) \hat{\Theta}_{MAP} = Argmax P(x_1,x_2,...,x_n|\Theta)P(\Theta) Θ^MAP=ArgmaxP(x1,x2,...,xn∣Θ)P(Θ)
2.1 Beta分布
在详细阐述MAP估计应用前,先简要介绍一下Beta分布及基本性质,先看百度百科的解释:
“贝塔分布(Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在机器学习和数理统计学中有重要应用。在概率论中,贝塔分布,也称Β分布,是指一组定义在(0,1) 区间的连续概率分布。”
其概率密度函数为:
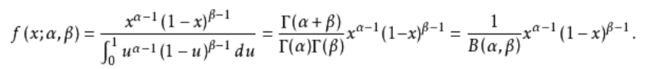
Beta分布定义域为(0,1),有两个参数α和β,其函数形状随参数的变化而变化。Beta分布实际常应用于模拟概率的分布,尤其是当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。这正好可以用来模拟我们MAP估计中,先验概率分布P(Θ)。下面给出B(β = 3,α = 4)的概率密度函数图像:

我们可以观察到该分布众数(mode)在0.6左右。若对其PDF函数关于X求导,我们可以得出Beta分的众数公式为:
M o d e = α − 1 α + β − 2 Mode = \frac{α-1}{α+β-2} Mode=α+β−2α−1
这个众数就好比我们的先验概率,换句话说,我们事前知道参数的取值大概率是在0.6左右的,我们通过调节α和β的取值来改变我们对于先验概率的认识。下图给出先验概率同为0.6的两个Beta分布的PDF:

虽然两个分布众数都为0.6,B(40,27)方差更小而B(4,3)方差较大。通俗地说,我们抛掷硬币67次得到40次正面使得我们对先验概率0.6的结论更加自信(不容易被更多样本数据所“稀释”!),而7次实验4次正面使得先验概率0.6没有那么可信,更容易被新的样本信息的摄入而改变我们对于未知参数的看法。
除了方便于我们模拟先验概率的分布这一特性,Beta分布其另一个重要性质是“其为伯努利分布和二项式分布的共轭先验分布的密度函数”,从而大大方便了我们的计算,这点留到下一小节具体阐述。
2.2 MAP估计实例
抛硬币十次,结果6正4反。假设如果正面朝上,随机变量X取1,反之取0,故我们得到一组样本
{1,1,1,1,1,1,0,0,0,0}。故样本的概率密度函数为:
P ( x 1 , x 2 , . . . , x 1 0 ∣ Θ ) = f ( x 1 , x 2 , x 3 , . . . . . . , x 1 0 , Θ ) = Θ 6 ( 1 − Θ ) 4 P(x_1,x_2,...,x_10|\Theta) = f(x_1,x_2,x_3,......,x_10,\Theta) =\Theta^{6}(1-\Theta)^{4} P(x1,x2,...,x10∣Θ)=f(x1,x2,x3,......,x10,Θ)=Θ6(1−Θ)4
假设我们的先验概率为0.7,取α = 22,β = 10 ,则先验概率密度函数为:
P ( Θ ) = B e t a ( 5 , 5 ) = Θ 21 ( 1 − Θ ) 9 B ( 22 , 10 ) P(\Theta)=Beta(5,5)=\frac{\Theta^{21}(1-\Theta)^9}{B(22,10)} P(Θ)=Beta(5,5)=B(22,10)Θ21(1−Θ)9
代入公式:
Θ ^ M A P = A r g m a x P ( x 1 , x 2 , . . . , x n ∣ Θ ) P ( Θ ) \hat{\Theta}_{MAP} = Argmax P(x_1,x_2,...,x_n|\Theta)P(\Theta) Θ^MAP=ArgmaxP(x1,x2,...,xn∣Θ)P(Θ)
得到:
Θ ^ M A P = A r g m a x Θ 6 ( 1 − Θ ) 4 Θ 21 ( 1 − Θ ) 9 B ( 22 , 10 ) = Θ 27 ( 1 − Θ ) 13 B ( 22 , 10 ) \hat{\Theta}_{MAP} = Argmax \Theta^{6}(1-\Theta)^4\frac{\Theta^{21}(1-\Theta)^9}{B(22,10)}=\frac{\Theta^{27}(1-\Theta)^{13}}{B(22,10)} Θ^MAP=ArgmaxΘ6(1−Θ)4B(22,10)Θ21(1−Θ)9=B(22,10)Θ27(1−Θ)13
仔细观察上式我们发现,P(X|Θ)与Beta(α=22,β=10)的乘积仍然是一个Beta分布,Beta(α=28,β=14)。Beta分布的这种性质就是上文提及的**“其与伯努利分布和二项分布的共轭性”,通俗地说,先验分布P(Θ)吸收了二项分布的样本信息后,调整过后的分布仍然是Beta分布**,这大大方便了我们的计算。
由于B(22,10)是常数,右边的式子取log对Θ求导,得到:
Θ M A P = 27 40 = 0.675 \Theta_{MAP} = \frac{27}{40}=0.675 ΘMAP=4027=0.675
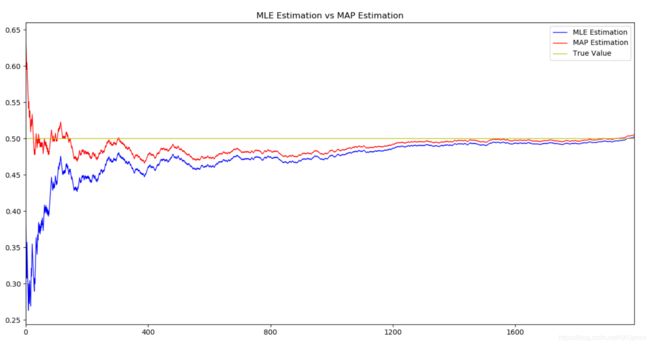
从结果可以看出,我们的先验概率0.7吸收了样本信息,得出了0.675的后验概率。若实验无限重复下去,MAP估计值和MLE估计值会不断逼近0.5(真实抛硬币概率),如下图(2000次投掷)。
3. Beyasian估计
贝叶斯估计是最大后验估计的进一步扩展,贝叶斯估计同样假定Θ是一个随机变量,但贝叶斯估计并不是直接估计出Θ的某个特定值,而是估计Θ的分布:
P ( Θ ∣ x 1 , x 2 , . . . , x n ) = P ( x 1 , x 2 , . . . , x n ∣ Θ ) P ( Θ ) ∫ Θ P ( x 1 , x 2 , . . . , x n ∣ Θ ) P ( Θ ) d Θ P(\Theta |x_1,x_2,...,x_n) = \frac{P(x_1,x_2,...,x_n|\Theta)P(\Theta)}{\int_{\Theta}P(x_1,x_2,...,x_n|\Theta)P(\Theta)d\Theta} P(Θ∣x1,x2,...,xn)=∫ΘP(x1,x2,...,xn∣Θ)P(Θ)dΘP(x1,x2,...,xn∣Θ)P(Θ)
可见贝叶斯估计的难点在于下方积分的计算。若是在上文的例子中,选用共轭分布作为先验概率,能使计算变得极为简洁;若不是则需要通过如蒙特卡洛积分等很多计算方法去计算。
3.1 Beyasian估计实例
还是以上的例子,掷硬币,得到6正4反,我们先用Beyasian方法估计Θ的分布:
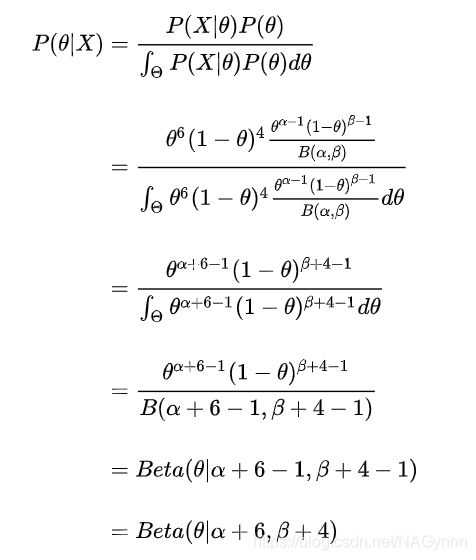
由于先验概率分布Beta分布的共轭性**(注:二项分布参数的共轭先验是Beta分布,多项式分布参数的共轭先验是Dirichlet分布,指数分布参数的共轭先验是Gamma分布,⾼斯分布均值的共轭先验是另⼀个⾼斯分布,泊松分布的共轭先验是Gamma分布)**,后验概率Θ仍为Beta分布。
所以使用贝叶斯估计,最佳估计量Θ为:
Θ B e y a s i a n = ∫ Θ Θ P ( Θ ∣ X ) d Θ = E [ Θ ] = α α + β \Theta_{Beyasian}=\int_{\Theta}\Theta P(\Theta|X)d\Theta= E[\Theta] = \frac{α}{α+β} ΘBeyasian=∫ΘΘP(Θ∣X)dΘ=E[Θ]=α+βα
使用MAP实例中的α和β值,得后验概率0.6875.
必须注意的是,Beyasian分布并不是为了计算参数的点估计值,而是用来估计新测量数据出现的概率,对于新出现的数据x_hat:
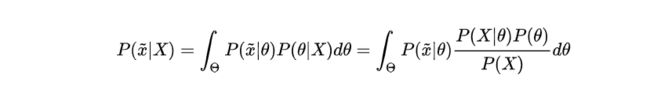
4. 总结
MLE和MAP估计都认为参数是个未知的固定值,区别在于MAP估计加入了参数的先验概率作为考虑因素,当参数的先验概率P(Θ)是(0,1)均匀分布时,两种估计方法相同。Beyasian方法将参数当作一个随机分量,计算的是参数在样本上的后验分布。
*Reference: *
[1]: “Ch.2 Estimating Probabilities: MLE and MAP”, Tom M. Mitchell
http://www.cs.cmu.edu/~tom/NewChapters.html
[2]: “贝叶斯估计、最大似然估计、最大后验概率估计”, SnailTyan
https://www.jianshu.com/p/9c153d82ba2d