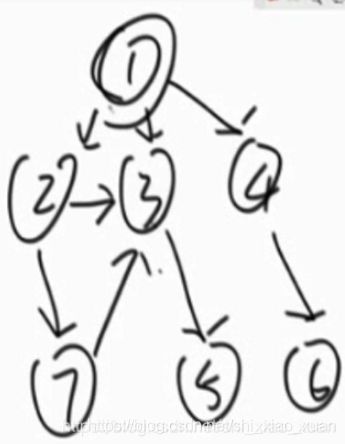
左神算法基础class6—题目3拓扑排序

1.题目：拓扑排序

拓扑排序算法适用范围：要求①有向图②有入度为0的节点③没有环

2.分析

在程序编译时，往往会有头文件互相依赖的情况，在图中箭头被指向的节点可以看做依赖于指向它的节点。如下图a依赖于b,c,d，而b又依赖c,k;d依赖k

那么拓扑排序的输出顺序是不依赖别的点的先输出。先输出k,c,删去k,c这时没有别的节点指向b,d了，输出b,d，最后，节点只剩下a再输出。
在图中可以用入度表示依赖情况，入度为零就是没有别的点指向它，可以先输出。输出后其指向的节点入度减一视为删去输出的点。
过程如下：
①为了方便查找，使用map存储节点与入度方便查找与修改入度（不能反过来），使用queue存储入度为零的节点用于暂存需要输出的点。
②遍历图中的所有节点，把所有入度为零的节点放入队列
③输出入度为零的节点
④把入度为零的节点所指向的节点的入度减一（相当于删去当前节点）若减一后入度为零加入队列
⑤在入度为0的队列不空的情况下重复③④

3.核心代码

list<Node*> sortedTopology(Graph graph)
{
     
	unordered_map<Node*,int> inMap;			//存储节点与入度 
	queue<Node*> zeroInQueue;				//存储入度为零的节点 
	unordered_map<int,Node*>::iterator ite = graph.nodes.begin();
	//遍历图中的所有节点，把所有入度为零的节点放入队列 
	while(ite != graph.nodes.end())								
	{
     
		inMap.insert(pair<Node*,int>(ite->second,ite->second->in));
		if(ite->second->in == 0)
			zeroInQueue.push(ite->second);
		ite++;
	}
	//输出入度为零的节点
	//把入度为零的节点所指向的节点的入度减一（相当于删去当前节点）
	//若又有入度为零的节点加入队列
	list<Node*> result;
	while(!zeroInQueue.empty())
	{
     
		Node* help = zeroInQueue.front();
		zeroInQueue.pop();
		result.push_back(help);
		cout<<help->value<<" ";
		for(Node* t : help->nexts)			 
		{
     
			if(--inMap.find(t)->second == 0)
				zeroInQueue.push(t);
		}
	}
	return result;
}

4.完整代码

#include 
#include "GraphGenerator.h"
#include "Node.h"
#include "Edge.h"
#include "Graph.h"
#include 
#include 
#include 
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
//拓扑排序 
list<Node*> sortedTopology(Graph graph)
{
     
	unordered_map<Node*,int> inMap;								//存储节点与入度 
	queue<Node*> zeroInQueue;									//存储入度为零的节点 
	unordered_map<int,Node*>::iterator ite = graph.nodes.begin();
	//遍历图中的所有节点，把所有入度为零的节点放入队列 
	while(ite != graph.nodes.end())								
	{
     
		inMap.insert(pair<Node*,int>(ite->second,ite->second->in));
		if(ite->second->in == 0)
			zeroInQueue.push(ite->second);
		ite++;
	}
	//输出入度为零的节点
	//把入度为零的节点所指向的节点的入度减一（相当于删去当前节点）
	//若又有入度为零的节点加入队列
	list<Node*> result;
	while(!zeroInQueue.empty())
	{
     
		Node* help = zeroInQueue.front();
		zeroInQueue.pop();
		result.push_back(help);
		cout<<help->value<<" ";
		for(Node* t : help->nexts)			 
		{
     
			if(--inMap.find(t)->second == 0)
				zeroInQueue.push(t);
		}
	}
	return result;
}
int main(int argc, char** argv) {
     
	
	vector<vector<int> > matrix= {
     {
     12,1,2},
								  {
     13,1,3},
								  {
     14,1,4},
								  {
     9,2,7},
								  {
     10,7,3},
								  {
     8,3,5},
								  {
     10,4,6}};
	GraphGenerator g;
	Graph graph = g.createGraph(matrix);
	sortedTopology(graph);
	return 0;
}

注：图的存储请见图的存储与表达中。

5.输出结果

应该打印：1,2,4,7,6,3,5