最短路径算法----Bellman-ford和SPFA算法
核心也是:对于边e(i,j), 如果w(i) + e(i,j) < w(j),就更新w(j)。这是一个松弛操作,即:估计的最短路径值渐渐地被更加准确的值替代,直至得到最优解(wiki)
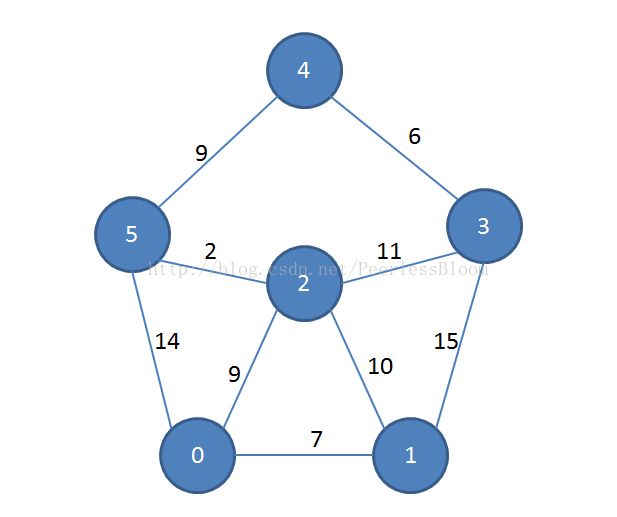
对于图
有
def bellman_ford(graph, start_node):
# graph:n*n matrix
# find min distance from start_node
length = len(graph)
s = {start_node:0} # the minimum distance between node i and v
# init s: O(Vertex)
for node in xrange(0, length):
if node == start_node:
continue
s[node] = max_int
# loose
# run (vertex - 1) times
for v in xrange(1, length):
# for every edge
for i in xrange(0, length):
for j in xrange(0, length):
if graph[i][j] != max_int and s[i] + graph[i][j] < s[j]:
s[j] = s[i] + graph[i][j]
return s使用二维矩阵表示图,时间复杂度是O(Vertex^3);
如果使用图数据结构,可以达到O(Vertex * Edge)
由于存在负权回路,还有一步检查的操作:
def test_negate_circle(graph, s):
# for every edge
length = len(graph)
for i in xrange(0, length):
for j in xrange(0, length):
if graph[i][j] != max_int and s[i] + graph[i][j] < s[j]:
return True
return False如果有负值回路,就说明永远能找到到目标点更小的一条边。
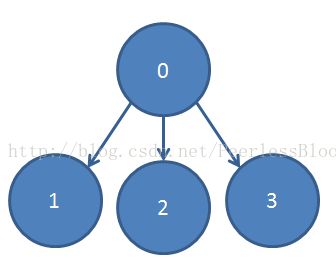
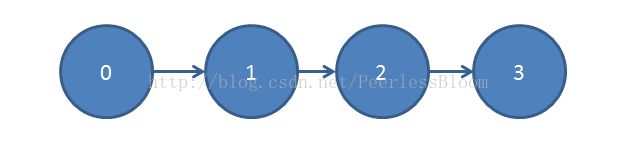
对于上面的第一张图,深度为1,显然只需要遍历一次边就能得到结果了。但是对于第二张图,在最坏的情况下,需要遍历3次才可以。
下面假设所有边的权值为1,人肉模拟一下最坏结果:
第一遍:u:{0:0, 1:1, 2:max_int, 3:max_int}
第二遍:u:{0:0, 1:1, 2:2, 3:max_int}
第三遍:u:{0:0, 1:1, 2:2, 3:3}
所以,遍历Vertex-1次可以改为:遍历所有边的最大深度。
什么是遍历所有边的最大深度?
从上图来看,如果用BFS遍历所有点得到图的深度为2:
第零层:0
第一层:1,2
第二层:3
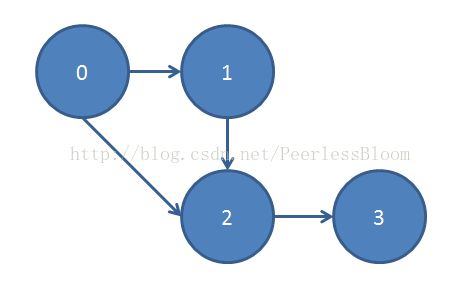
但是实际上,可能存在0->1->2->3,使得0~3的距离最短。
遍历所有边的最大深度的结果则是:
第零层:0
第一层:1[e(0,1)],2[e(0,2)]
第二层:2[e(1,2)]
第三层:3[e(2,3)]
这个层数只是估算出来的最坏情况,也就是循环次数的上界
实际上,如果在一次遍历所有的边的时候,没有松弛操作,那么继续遍历也没有意义了。
这就是SPFA的思想:松弛操作必定只会发生在最短路径前导节点松弛成功过的节点上,用一个队列记录松弛过的节点,可以避免了冗余计算。
也就是说,只有对更新过的w(i),才有可能出现w(i) + e(i,j) < w(j)。第一个更新的就是开始节点啦,更新后的权重为0。
def SPFA(graph, start_node):
length = len(graph)
s = {i:max_int for i in xrange(0, length)}
s[start_node] = 0
queue_loose = deque([start_node])
circle_tester = defaultdict(lambda : 0)
while queue_loose:
i = queue_loose.popleft()
# update s
for j in xrange(0, length):
if graph[i][j] != max_int and s[i] + graph[i][j] < s[j]:
s[j] = s[i] + graph[i][j]
queue_loose.append(j)
# test circle
circle_tester[j] += 1
if circle_tester[j] == length:
# has negate circle
return None
return s负权环的检测我也写在SPFA里面了,如果一个节点访问次数大于Vertex次,就认为有环。
原因我猜想是:最多有Vextex-1个节点(除去自己)会对某个节点产生影响,如果大于这个数,说明有负环。
如果不对,希望大家提出指正~谢谢
驱动
graph = [[0, 7, 9, max_int, max_int, 14],
[7, 0, 10, 15, max_int, max_int],
[9, 10, 0, 11, max_int, 2],
[max_int, 15, 11, 0, 6, max_int],
[max_int, max_int, max_int, 6, 0, 9],
[14, max_int, 2, max_int, 9, 0]]
print SPFA(graph, 0)