MEMS惯性传感器初始姿态角的确定
9轴MEMS惯性传感器初始姿态角的计算
随着微机电系统( Micro Electromechanical System,MEMS) 技术的不断发展,基于MEMS的惯性传感器得到了更加广泛的应用,比如机器人跟踪导航,行人定位。惯性导航系统利用初始的位置、速度和姿态信息,通过陀螺仪和加速度测量的角速率和比力进行二次积分推算得到目标的位置、速度和姿态信息。因此,初始对准的好坏将确定惯性导航系统的精度和稳定性。
MEMS惯性传感器中加速度计的精度通常优于1mg,而陀螺仪无法敏感到地球自转,因此可以利用加速度计确定惯性导航系统的横滚角和俯仰角,但却无法利用陀螺仪确定航向角信息。利用磁力计能确定惯性导航系统的初始航向角
导航坐标系和载体坐标系之间的关系
这里的导航坐标系采用北向-东向-地向(NED)坐标系,记为n系;载体坐标系采用前向-右向-向下坐标系,记为b系。绕着载体的 x \ x x轴旋转为横滚角,绕着载体的 y \ y y轴旋转为俯仰角,绕着载体的 z \ z z轴旋转为航向角。导航坐标系依次沿着 x \ x x轴、 y \ y y轴和 z \ z z轴旋转能变换到载体坐标系中,那么载体坐标系和导航坐标系的姿态旋转矩阵DCM可表示为:
C b n = [ c o s θ c o s ψ − c o s ϕ s i n ψ + s i n ϕ s i n θ c o s ψ s i n ϕ s i n ψ + c o s ϕ s i n θ c o s ψ c o s θ s i n ψ c o s ϕ c o s ψ + s i n ϕ s i n θ s i n ψ − s i n ϕ c o s ψ + c o s ϕ s i n θ s i n ψ − s i n θ s i n ϕ c o s θ c o s ϕ c o s θ ] \ C{^n_b} = \begin{bmatrix} {cos\theta cos \psi} & {-cos\phi sin \psi +sin\phi sin\theta cos \psi} & {sin\phi sin \psi +cos\phi sin\theta cos \psi} \\ {cos\theta sin\psi} & {cos\phi cos\psi +sin\phi sin\theta sin\psi} & {-sin\phi cos\psi +cos\phi sin\theta sin\psi} \\ {-sin\theta} & {sin\phi cos\theta} &{cos\phi cos\theta} \end{bmatrix} Cbn=⎣⎡cosθcosψcosθsinψ−sinθ−cosϕsinψ+sinϕsinθcosψcosϕcosψ+sinϕsinθsinψsinϕcosθsinϕsinψ+cosϕsinθcosψ−sinϕcosψ+cosϕsinθsinψcosϕcosθ⎦⎤其中, θ \theta θ为俯仰角, ϕ \phi ϕ为横滚角, ψ \psi ψ为航向角。
注:选择的导航坐标系和载体坐标系和这里的不一致,以及旋转顺序和这里的不一致,所产生的旋转矩阵均不相同。
注:坐标系统和姿态旋转矩阵是惯性导航系统最基础最核心的部分。
初始横滚角和俯仰角的计算
当传感器静止时,加速度计测量的是重力在载体坐标系下的投影。由于是MEMS传感器器件误差较大,可以不考虑重力在北方向和东方向的投影,即不考虑重力的垂线偏差,那么重力和加速度计的比力(加速度)之间的关系为:
f i b b = C n b g n f^b_{ib} = C{^b_n}g^n fibb=Cnbgn其中, f i b b = [ f i b , x b f i b , y b f i b , z b ] ′ f^b_{ib}=\begin{bmatrix} f^b_{ib,x} &f^b_{ib,y}&f^b_{ib,z} \end{bmatrix}' fibb=[fib,xbfib,ybfib,zb]′为加速度计输出的x,y和z轴的比力(或加速度)信息, g n = [ 0 0 g D n ] ′ g^n=\begin{bmatrix} 0 &0&g^n_D \end{bmatrix}' gn=[00gDn]′为导航坐标系下重力在北(North)、东(East)和地(Down)方向三个的投影。通过上面DCM矩阵可以展开为:
[ f i b , x b f i b , y b f i b , z b ] = [ − s i n θ − c o s θ s i n ϕ − c o s θ c o s ϕ ] g D n . . . . . . ( 1 ) \begin{bmatrix} f^b_{ib,x} \\f^b_{ib,y}\\f^b_{ib,z} \end{bmatrix}=\begin{bmatrix} -sin\theta \\-cos\theta sin\phi \\-cos\theta cos\phi \end{bmatrix}g^n_D \space ......(1) ⎣⎡fib,xbfib,ybfib,zb⎦⎤=⎣⎡−sinθ−cosθsinϕ−cosθcosϕ⎦⎤gDn ......(1)通过公式(1)可以计算静止期间惯性传感器的初始横滚角和俯仰角,计算公式为:
θ = a t a n ( f i b , x b f i b , y b ∗ f i b , y b + f i b , z b ∗ f i b , z b ) , ϕ = a t a n 2 ( − f i b , y b , − f i b , z b ) \theta=atan(\cfrac{f^b_{ib,x}}{\sqrt{\smash[b]{{f^b_{ib,y}*{f^b_{ib,y}+{f^b_{ib,z}*{f^b_{ib,z} }}}}}}}) \space, \phi=atan2(-f^b_{ib,y},-f^b_{ib,z}) θ=atan(fib,yb∗fib,yb+fib,zb∗fib,zbfib,xb) ,ϕ=atan2(−fib,yb,−fib,zb)
初始磁航角的计算
由于陀螺仪无法敏感到地球自转,因此可通过磁力计确定初始的航向角。当传感器静止时,测力计测量的是地磁场在载体坐标系下的投影。磁力计量测的磁场和地磁场之间的关系可表示为:
m n = C b , p r n m b m^n=C{^n_{b,pr}}m^b mn=Cb,prnmb其中, m n = [ m x n m y n m z n ] ′ m^n=\begin{bmatrix} m^n_x &m^n_y&m^n_z \end{bmatrix}' mn=[mxnmynmzn]′为地磁场, m b = [ m x b m y b m z b ] ′ m^b=\begin{bmatrix} m^b_x &m^b_y&m^b_z \end{bmatrix}' mb=[mxbmybmzb]′为磁力计测量的磁场。在通过加速度计确定横滚角和俯仰角之后,姿态转换矩阵DCM可以表示为:
C b , p r n = [ c o s θ s i n ϕ s i n θ c o s ϕ s i n θ 0 c o s ϕ − s i n ϕ − s i n θ s i n ϕ c o s θ c o s ϕ c o s θ ] C{^n_{b,pr}} =\begin{bmatrix} cos\theta & sin\phi sin\theta &cos\phi sin\theta \\ 0 & cos\phi& -sin\phi \\ {-sin\theta} & {sin\phi cos\theta} &{cos\phi cos\theta} \end{bmatrix} Cb,prn=⎣⎡cosθ0−sinθsinϕsinθcosϕsinϕcosθcosϕsinθ−sinϕcosϕcosθ⎦⎤磁航角的计算公式为: c o s ψ m = − a t a n 2 ( m y n , m x n ) cos {\psi_m} = -atan2(m^n_y,m^n_x) cosψm=−atan2(myn,mxn)那么磁航角计算公式可进一步表示为:
c o s ψ m = − a t a n 2 ( m y b c o s ϕ − m z b s i n ϕ , m x b c o s θ + m y b s i n ϕ s i n θ + m z b c o s ϕ s i n θ ) cos {\psi_m} = -atan2(m^b_ycos\phi-m^b_zsin\phi,m^b_xcos\theta+m^b_ysin\phi sin\theta+m^b_zcos\phi sin\theta) cosψm=−atan2(mybcosϕ−mzbsinϕ,mxbcosθ+mybsinϕsinθ+mzbcosϕsinθ)
初始航向角的计算
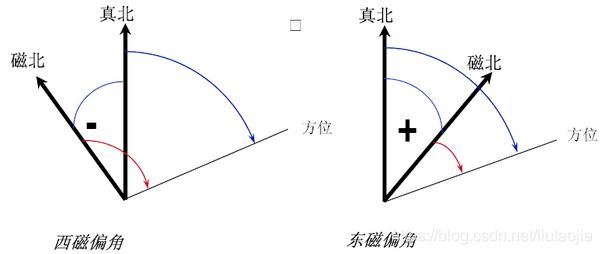
由于地理北极和磁力北极之间存在一个磁偏角,惯性导航中初始的航向角是以地理北极(真北)进行计算的,因此计算初始航向角的时候需要减去磁偏角。磁偏角可以通过查表或者公式计算出来(一个城市内磁偏角相同)。
磁北和真北(地理北极)之间的关系可以通过下图表示
磁偏角可以通过该网址查询[武汉的磁偏角为-4°26′]:magnetic-declination: http://www.magnetic-declination.com/