简记AlexNet
《简记AlexNet》
文章《ImageNet Classification with Deep Convolutional Neural Networks》介绍的网络结构,是早期的经典结构,在2012年以较大优势夺得ImageNet竞赛的冠军,作者是Hiton的学生。
Key Words:ReLU、LRN、Overlapping Pooling、Drop out
Beijing, 2020
作者:多伦多大学的Alex Krizhevsky等人
Paper:http://www.cs.toronto.edu/~fritz/absps/imagenet.pdf
Agile Pioneer
模型介绍
作为早期经典模型,其模型大小达到了240MB。
该模型有5个卷积层,3个池化层和3个全连接层,比之前的网络更深,因为使用多GPU训练,所以第一层卷积后有两个完全一样的分支,用以加速训练。
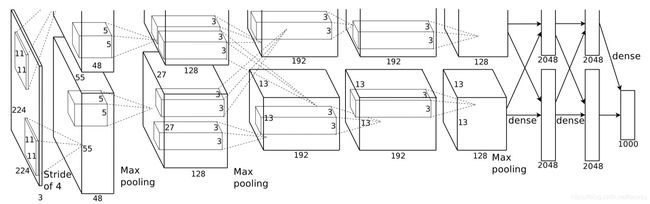
我觉得这个图画的不好,容易让人误解,以为网络是由两部分组成的,我当时作为初学者第一次接触的时候就产生了误解,实际上是第一层的96个卷积核,分到了两片GPU上做运算了,每片负责运算48个核,卷积核大小为11x11,此后的层就分到了两片GPU上做运算了。
-
第一层: 卷积层1,输入为 224×224×3224 \times 224 \times 3224×224×3的图像,卷积核的数量为96,论文中两片GPU分别计算48个核; 卷积核的大小为 11×11×311 \times 11 \times 311×11×3; stride = 4, stride表示的是步长, pad = 0, 表示不扩充边缘;
-
卷积后的图形大小是怎样的呢?
- wide = (224 + 2 * padding - kernel_size) / stride + 1 = 54
- height = (224 + 2 * padding - kernel_size) / stride + 1 = 54
- dimention = 96
然后进行 (Local Response Normalized), 后面跟着池化pool_size = (3, 3), stride = 2, pad = 0 最终获得第一层卷积的feature map
-
最终第一层卷积的输出为 27 x 27 x 96
-
第二层: 卷积层2, 输入为上一层卷积的feature map, 卷积的个数为256个,论文中的两个GPU分别有128个卷积核。卷积核的大小为:5×5×485 \times 5 \times 485×5×48; pad = 2, stride = 1; 然后做 LRN, 最后 max_pooling, pool_size = (3, 3), stride = 2;
-
第三层: 卷积3, 输入为第二层的输出,卷积核个数为384, kernel_size = (3×3×2563 \times 3 \times 2563×3×256), padding = 1, 第三层没有做LRN和Pool
-
第四层: 卷积4, 输入为第三层的输出,卷积核个数为384, kernel_size = (3×33 \times 33×3), padding = 1, 和第三层一样,没有LRN和Pool
-
第五层: 卷积5, 输入为第四层的输出,卷积核个数为256, kernel_size = (3×33 \times 33×3), padding = 1。然后直接进行max_pooling, pool_size = (3, 3), stride = 2;
-
第6,7,8层是全连接层 ,每一层的神经元的个数为4096,最终输出softmax为1000,所以这部分的参数量很大,ImageNet这个比赛的分类个数为1000。全连接层中使用了RELU和Dropout。
网络架构
Pytorch 实现代码如下:
class AlexNet(nn.Module):
def __init__(self, num_classes=NUM_CLASSES):
super(AlexNet, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(1, 96, kernel_size=11,padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2),
nn.Conv2d(96, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2),
nn.Conv2d(256, 384, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(384, 384, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(384, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2),
)
self.classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(256 * 2 * 2, 4096),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(4096, 4096),
nn.ReLU(inplace=True),
nn.Linear(4096, 10),
)
def forward(self, x):
x = self.features(x)
x = x.view(x.size(0), 256 * 2 * 2)
x = self.classifier(x)
return x
核心思想
-
采用ReLU激活函数
-
局部响应归一化LRN,简单来说就是第i个通道上的x, y位置的激活函数的输出要除以沿着通道方向的相邻 n/2 半径的通道同位置元素的平方和的beta次方
b x , y i = a x , y i / ( k + α ∑ j = m a x ( 0 , i − n / 2 ) m i n ( N − 1 , i + n / 2 ) ( a x , y j ) 2 ) b^i_{x,y} = a^i_{x,y} / (k + \alpha \sum^{min(N - 1, i + n / 2)}_{j = max(0, i - n / 2)}(a^j_{x,y})^2) bx,yi=ax,yi/(k+αj=max(0,i−n/2)∑min(N−1,i+n/2)(ax,yj)2)
后来,在2015年 Very Deep Convolutional Networks for Large-Scale Image Recognition中提到LRN基本没什么用。
-
Overlapping Pooling (stride < pool_size),论文中说,在训练模型过程中,覆盖的池化层更不容易过拟合。
-
引入Drop out
-
数据增强
-
多GPU并行
总结&思考
Q1:论文中提到的saturating neurons与non-saturating neurons的区别?
A1:
- non-saturating neurons = 没有被挤压(到一个特定的区间)处理过的值
- saturating neurons = 被挤压(到一个特定的区间)过的值
似乎谈论saturating neurons 和 non-saturating neurons的场景都会有non-linear activation的身影,这里可以将non-linear activations分为两类:
-
输出saturating neurons的activation:
- sigmoid: input neurons的值会被挤压到[0,1]的区间
- tanh:input neurons的值会被挤压到[-1,1]的区间
-
输出non-saturating neurons 的activation:
- relu:input neurons的值,要么变0, 要么保持原值(无挤压,无最大最小值限制)
- leaky_relu:input neurons的值, 要么按照某比例缩小,要么保持原值(无挤压,无最大最小值限制)
Q2: 为什么要用relu这样的能生成non-saturating neurons的non-linear activations, 而不用生成saturating neurons的sigmoid或tanh?
A2:
- 规避vanishing, exploding of gradients 带来的gradient值过大过小,导致训练效率低下

- 如上图所示,使用了RELU后(实线),对比tanh(虚线),训练效率大幅提升(但论文中似乎没有提及规避vanishing, exploding of gradients的问题)
Q3:最后,回头问一句,什么是saturation? 为什么要叫saturating, non-saturating?
A3:
- 因为有一个数学计算叫做saturation arithmetic
- 这个算法就是要求将input的值全部变成在某个最大值和最小值之间的值