机器学习——Python实战单变量线性回归

单变量线性回归的实战

本文主要进行用Python单变量线性回归的一个入门实战（吴恩达机器学习练习1）。
讲在前面：进行机器学习，首先要对使用Python进行数据分析非常熟悉，因为机器学习要与数据作斗争，当然用Matlab也可以进行机器学习中的运算，对于我个人我还是比较喜欢用Python。我会尽量把代码描述的详细一点，并且实时展示每一步操作后数据的情况。话不多说，开始吧！

问题简述

你将使用单变量预测食品卡车利润。假设你是一家餐厅的CEO，并正在考虑在不同的城市开设一个新的分店。这个餐厅在各个城市都有餐车，你有城市的利润和人口数据，你可以使用此数据帮助选择下一个要扩展的城市。文件ex1data1.txt包含线性回归问题的数据集。第一列是城市人口，第二列是那个城市的一辆食品卡车的利润。利润负值表示损失。
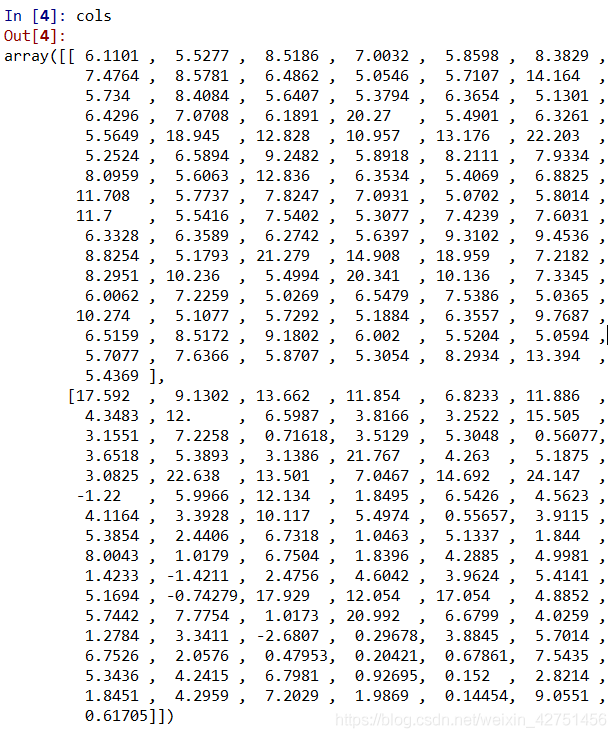
我们来看一下给出的数据集：

第一列是城市人口数量，第二列是该城市对应的餐车利润。

解决问题

单变量线性回归，我们需要定义假设函数、代价函数以及使用梯度下降算法，公式在上一篇博客里面有讲过，接下来我们开始一步一步操作。对了，我个人使用的Jupyter Notebook，它比较易于调试和交互。

1.导入数据以及必要的库

import numpy as np
import matplotlib.pyplot as plt

data = 'ex1data1.txt'

2.对数据进行初步整理

我们使用numpy的loadtxt来导入数据，我已注释至代码块。

cols = np.loadtxt(data,delimiter=',',usecols=(0,1),unpack=True) 
# delimiter用于分隔值
#usecols(0,1)代表读取第1列，第2列
#unpack是指会把每一列当成一个向量输出而不是合并在一起
X = np.transpose(np.array(cols[:-1]))
y = np.transpose(np.array(cols[-1:]))
#X矩阵和y向量
m = y.size #训练集的数量
X = np.insert(X,0,1,axis=1)

我们来看一下数据每一步都是什么样的吧！

1. cols

2. X矩阵和y向量

3. m

3.对数据进行可视化

我们使用matplotlib来对我们的训练集进行可视化

plt.figure(figsize=(10,6)) # 以长10英寸，宽10英寸的大小创建一个窗口
plt.plot(X[:,1],y[:,0],'r.',markersize=10)
plt.grid(True)
plt.ylabel('Profit')
plt.xlabel('Population of city')

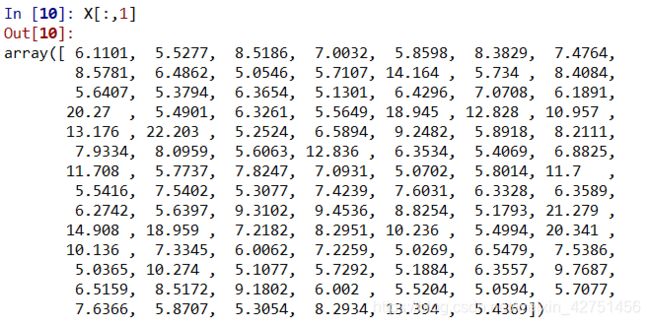
你可能会有疑问，X[:,1]又是什么？它指的是我们使用X的第二列，看下图：

我们来看一下我们可视化的结果：

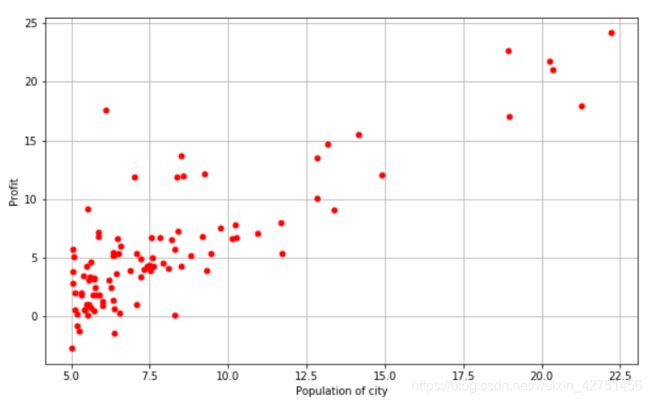
关于matplotlib如果你还有不懂的可以上百度查一下这个模块。

4.定义假设函数以及代价函数

iterations = 1500 # 设置梯度下降的迭代次数
alpha = 0.01 # 设置梯度下降的学习率

def Hypothesis(theta,X):
    return np.dot(X,theta) # 定义线性回归的假设函数

def costFunction(mytheta,X,y): # 定义代价函数
    return float((1./(2*m)) * np.dot((Hypothesis(mytheta,X)-y).T,(Hypothesis(mytheta,X)-y)))

initial_theta = np.zeros((X.shape[1],1))
print(costFunction(initial_theta,X,y))

这一段就不用过多说了，根据上一篇博客我说的公式就可以编写出函数，如果对numpy模块不太了解可以上百度查一下。我们设置迭代次数以及学习率，让θ的初始值为0并且带入代价函数，打印的结果如下：

5.定义梯度下降

def gradientDescent(X,theta_start=np.zeros(2)):
    theta = theta_start
    jVec = []
    thetaHistory = []
    for i in range(iterations):
        tmptheta = theta
        jVec.append(costFunction(theta,X,y))
        thetaHistory.append(list(theta[:,0]))
        for j in range(len(tmptheta)):
            tmptheta[j] = theta[j] - (alpha/m)*np.sum((Hypothesis(initial_theta,X) - y)*np.array(X[:,j]).reshape(m,1))
        theta = tmptheta
    return theta,thetaHistory,jVec

这里对其中一些变量解释一下：

jVec是用来记录代价函数迭代的过程的，方便我们可视化。
thetaHistory是用来记录我们尝试的θ的值。

如果这一块有问题，那么多半是像我刚开始一样对梯度下降的过程不太清楚，多思考一下想通了就好了。。

6.运行梯度下降得到最优解并使其过程可视化

initial_theta = np.zeros((X.shape[1],1))
theta,thetaHistory,jVec = gradientDescent(X,initial_theta)
def plotConvergence(jVec):
    plt.figure(figsize=(10,6))
    plt.plot(range(len(jVec)),jVec,'bo')
    plt.grid(True)
    plt.title('Convergence of Cost Function')
    plt.xlabel("Iteraions Number")
    plt.ylabel('Cost Function')
    dummy = plt.xlim([-0.05*iterations,1.05*iterations])
    
    
plotConvergence(jVec)
dummy = plt.ylim([4,7])

我们给θ一个初始值0，再直接运行梯度下降。其实这一部分主要是可视化的，运行梯度下降只用了两行。梯度下降的过程都在上一块，那我们看一下我们的各个变量：

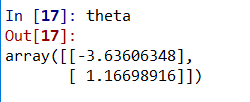
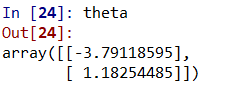
最优解θ（迭代次数不同这里可能不同）：

如果将迭代次数调至2000则θ如下：

θ的历史值：

实在太多了，毕竟设置了1500次迭代。

剩下的就是可视化了，我们直接来看代价函数的收敛过程吧！

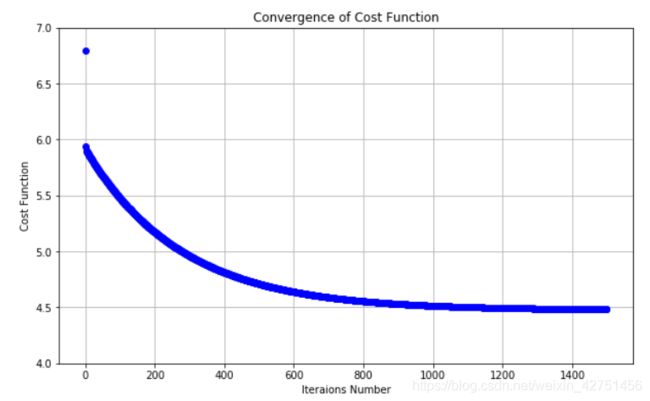
可以看出迭代次数在1200-1400之后就趋于平缓，所以设置1500次是可行的。

7.用得出的最优解θ拟合数据

def myfit(xVal):
    return theta[0] + theta[1]*xVal

plt.figure(figsize=(10,6))
plt.plot(X[:,1],y[:,0],'r.',markersize=10,label='Training Data')
plt.plot(X[:,1],myfit(X[:,1]),'b-',label='Hypothesis:h(x) = %0.2f + %0.2fx'%(theta[0],theta[1]))
plt.grid(True)
plt.ylabel('Profit in $10,000s')
plt.xlabel('Population of city in $10,000s')
plt.legend()

这一部分基本就是可视化的过程，把θ应用进去得出直线，查看拟合情况。结果如下：

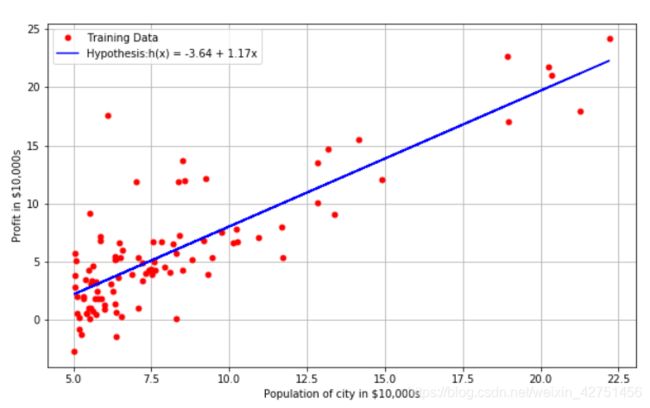
从可视化的结果来看我们拟合的还是差不多的，那么问题来了，如果你是这家餐馆的CEO，你会选在哪个城市开下家分店？

8.结语

可以看出单变量解决问题有点不太准确，开分店还和别的因素有关，比如城市的消费水平，政府政策等等，单就这个例子来说单变量肯定没有多变量准确。

好了这个实战就说到这里啦，如果你有问题请留言，我会第一时间回复。本人也是一名学生，写文章的同时肯定会有错误发生，还请多多包容，指出错误。下一篇我会写多变量线性回归，问题和建议请联系：[email protected]

还请您关注公众号第一时间获取文章，更轻松地与我联系！

感谢您的阅读！如果觉得有用不妨分享给其他朋友哦~如需转载，请注明原文出处，作者：vergilben