c++ 数据结构 图的应用（实现图的深度优先和广度优先遍历）——以邻接表为存储结构

数据结构实习——图及应用（图的遍历）

一、问题描述

很多涉及图上操作的算法都是以图的遍历操作为基础的。试写一个程序，演示无向图的遍历操作。

二、基本要求

以邻接表为存储结构，实现连通无向图的深度优先和广度优先遍历。以用户指定的结点为起点，分别输出每种遍历下的结点访问序列和相应生成树的边集。

三、实现提示

设图的结点不超过30个，每个结点用一个编号表示（如果一个图有n个结点，则它们的编号分别为1，2，…，n）。通过输入图的全部边输入一个图，每个边为一个数对，可以对边的输入顺序做出某种限制。注意，生成树的边是有向边，端点顺序不能颠倒。

四、测试数据

1、测试单个结点且没有边
2、测试如下图所示的图的遍历结果

五、设计思想

本题要求我们以邻接表为存储结构，实现连通无向图的深度优先和广度优先遍历，下面分别讲述邻接表、深度优先遍历和广度优先遍历。
1、邻接表
邻接表是类似于树的孩子链表。顺序存储结构与链式存储相结合。对图G中Vi，将邻接于Vi的顶点链成一个单链表，即邻接表，再将邻接表表头放到数组中，构成图的邻接表。

2、无向图深度优先遍历
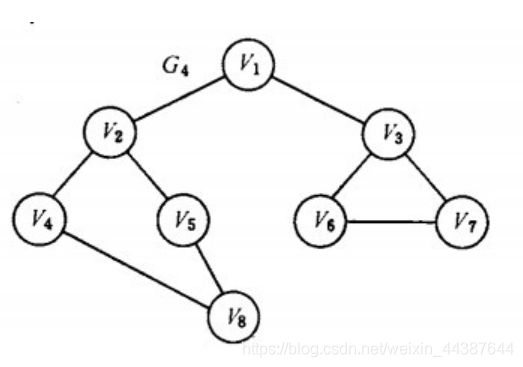
针对本次的测试数据2，从顶点搜索，访问顶点v1，选择未曾访问的邻接点v2。从v2出发，选择未曾访问的邻接点v4，以此类推，v4，v8，v5搜索。在访问了v5之后，邻接点12458都被访问，回到v8。最后回到v1。然后又从v1搜索v3。
结果：
v1–>v2–>v4–>v8–>v5–>v3–>v6–>v7

3、无向图广度优先遍历
广度优先遍历可以说是按照图的层次结构遍历。访问一个点，将该店未被访问的邻接点依次全部访问，记录最早被访问的点，从这个点出发，该店未被访问的邻接点依次全部访问……循环最终都被访问过。
如图，先访问v1和邻接点v2和v3，然后访问v2的邻接点v4和v5及v3的邻接点v6和v7，最后访问v4的邻接点v8。此时所有顶点都被访问，结束遍历。
结果：
v1–>v2–>v3–>v4–>v5–>v6–>v7–>v8

六、设计图示

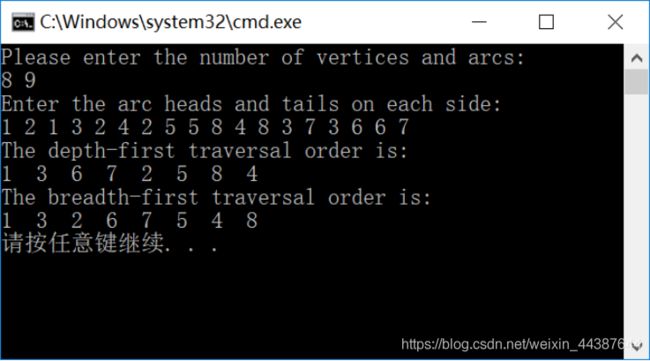
七、测试结果

1、

2、

八、测试结果分析

根据测试出的结果显示，我测试出的结果，与我预期的结果不一致，通过调试，我发现 我的程序编写和算法设计，基本没什么问题，或者说应该没有什么严重的问题，而且，测试的结果理论上也是可以得到的。
从理论上来讲，图的深度优先遍历和广度优先遍历是不唯一的，因为，只需判断下一个结点有没有被访问过，如果都没被访问过，所以访问哪个都是可以的，但是，如果算法确定了，图中点和边的存储顺序确定了，那访问顺序也是确定的，所以，我暂时还没有找到解决这一问题的方法，不过，程序本身和测试结果都是正确的，也算是完成了本次实习任务。、

九、附录

【源代码】

#include "stdafx.h"
#include
using namespace std;

#define MAX_VERTEX_NUM 30           //图的最大顶点数不超过30个
#define MAXQSIZE 40                 //队列的最大容量

enum BOOL{
      False, True };

typedef struct ArcNode
{
     
	int adjvex;                      //顶点位置
	struct ArcNode *nextarc;         //指向下一条弧的指针
}ArcNode;                            //弧结点

typedef struct{
     
	ArcNode* AdjList[MAX_VERTEX_NUM];            //指向第一条依附该顶点的弧的指针
	int vexnum, arcnum;                          //图的当前顶点和弧数
}Graph;

typedef struct                       //队列结构
{
     
	int elem[MAXQSIZE];              //数据域
	int front;                       // 队头指针
	int rear;                       // 队尾指针
}SqQueue;

BOOL visited[MAX_VERTEX_NUM];       //全局变量——访问标志数组
void CreateGraph(Graph &);          //生成图的邻接表
void DFSTraverse(Graph);            //深度优先搜索遍历图
void DFS(Graph, int);
void BFSTraverse(Graph);            //广度优先搜索遍历图
void Initial(SqQueue &);            //初始化一个队列
BOOL QueueEmpty(SqQueue);           //判断队列是否为空
BOOL EnQueue(SqQueue &, int);       //将一个元素入队列
BOOL DeQueue(SqQueue &, int &);     //将一个元素出队列
int firstAdjVex(Graph, int);        //求图中某一顶点的第一个邻接顶点
int NextAdjVex(Graph, int, int);    //求某一顶点的下一个邻接顶点

void CreateGraph(Graph &G){
     
	//构造邻接表结构的图G
	int i;
	int start, end;
	ArcNode *s;
	for (i = 1; i <= G.vexnum; i++)
		G.AdjList[i] = NULL;                              //初始化指针数组
	if (G.arcnum == 0){
     
		cout << "The graph have no edges." << endl;
	}
	else{
     
		for (i = 1; i <= G.arcnum; i++)
		{
     
			cin >> start >> end;                              //输入弧的起点和终点
			s = (ArcNode *)malloc(sizeof(ArcNode));           //生成一个弧结点
			s->nextarc = G.AdjList[start];                    //插入到邻接表中
			s->adjvex = end;
			G.AdjList[start] = s;
			{
     
				s = (ArcNode *)malloc(sizeof(ArcNode));
				s->nextarc = G.AdjList[end];
				s->adjvex = start;
				G.AdjList[end] = s;
			}
		}
	}
}

void DFSTraverse(Graph G)
{
     
	//深度优先遍历图G
	int i;
	cout << "The depth-first traversal order is:" << endl;
	for (i = 1; i <= G.vexnum; i++)
		visited[i] = False;               //访问标志数组初始化
	for (i = 1; i <= G.vexnum; i++)
	if (!visited[i]) DFS(G, i);
	cout << endl;
}

void DFS(Graph G, int i){
     
	//从第i个顶点出发递归地深度遍历图G
	int w;
	visited[i] = True;                                             //访问第i个顶点
	cout << i <<"  ";
	for (w = firstAdjVex(G, i); w > 0; w = NextAdjVex(G, i, w))
	if (!visited[w]) DFS(G, w);                                    //对尚未访问的邻接顶点w调用DFS
}

void BFSTraverse(Graph G){
     
	//按广度优先非递归的遍历图G，使用辅助队列Q和访问标志数组visited
	int i, u, w;
	SqQueue	Q;
	cout << "The breadth-first traversal order is:" << endl;
	for (i = 1; i <= G.vexnum; i++) visited[i] = False;                        //访问标志数组初始化
	Initial(Q);                                                                //初始化队列
	for (i = 1; i <= G.vexnum; i++)
	if (!visited[i])
	{
     
		visited[i] = True;                                                      //访问顶点i
		cout << i<< "  ";
		EnQueue(Q, i);                                                          //将序号i入队列
		while (!QueueEmpty(Q))                                                  //若队列不空，继续
		{
     
			DeQueue(Q, u);                                                      //将队头元素出队列并置u
			for (w = firstAdjVex(G, u); w > 0; w = NextAdjVex(G, u, w))
			if (!visited[w])                                                    //对u的尚未访问的邻接顶点w进行访问并入队列
			{
     
				visited[w] = True;
				cout << w << "  ";
				EnQueue(Q, w);
			}
		}
	}
	cout << endl;
}

int firstAdjVex(Graph G, int v)
{
     
	//在图G中寻找第v个顶点的第一个邻接顶点
	if (!G.AdjList[v])
		return 0;
	else
		return(G.AdjList[v]->adjvex);
}

int NextAdjVex(Graph G, int v, int u)
{
     
	//在图中寻找第v个顶点的相对于u的下一个邻接顶点
	ArcNode *p;
	p = G.AdjList[v];
	while (p->adjvex != u) p = p->nextarc;                    //在顶点v的弧链中找到顶点u
	if (p->nextarc == NULL)
		return 0;                                             //若已经是最后一个结点，返回0
	else
		return(p->nextarc->adjvex);                           //返回下一个邻接顶点的序号
}

void Initial(SqQueue &Q)
{
     
	//队列初始化
	Q.front = Q.rear = 0;
}

BOOL QueueEmpty(SqQueue Q){
     
	//判断队列是否已空，若空返回True,否则返回False
	if (Q.front == Q.rear)
		return True;
	else
		return False;
}

BOOL EnQueue(SqQueue &Q, int ch)
{
     
	//入队列，成功返回True,失败返回False
	if ((Q.rear + 1) % MAXQSIZE == Q.front)
		return False;
	Q.elem[Q.rear] = ch;
	Q.rear = (Q.rear + 1) % MAXQSIZE;
	return True;
}

BOOL DeQueue(SqQueue &Q, int &ch)
{
     
	//出队列，成功返回True,并用ch返回该元素值，失败返回False
	if (Q.front == Q.rear)
		return False;
	ch = Q.elem[Q.front];
	Q.front = (Q.front + 1) % MAXQSIZE;
	return True;//成功出队列，返回True
}

void main(){
     
	Graph G;                        //采用邻接表结构的图
	
	cout << "Please enter the number of vertices and arcs:" << endl;
	cin >> G.vexnum >> G.arcnum;

	cout << "Enter the arc heads and tails on each side:" << endl;
	CreateGraph(G);

	DFSTraverse(G);
	BFSTraverse(G);


	//cout << "Please enter any number to finish running.";
	int stay;
	cin >> stay;  //由于要上交.exe可执行文件，程序完执行，就会自动关闭了，这里是临时增加的停留操作，让执行结果在窗口中停留

}