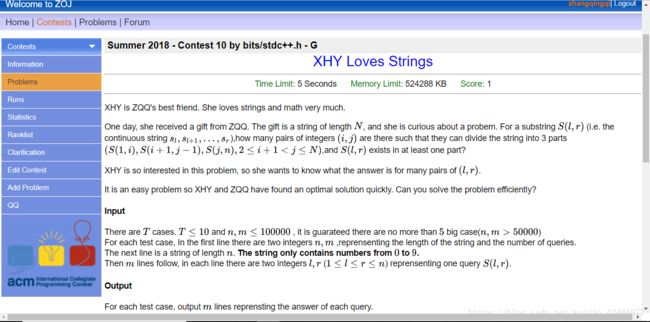
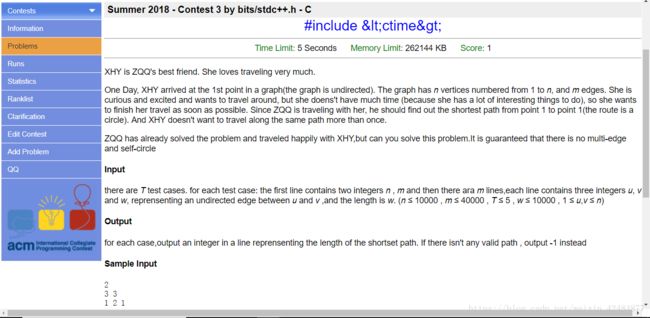
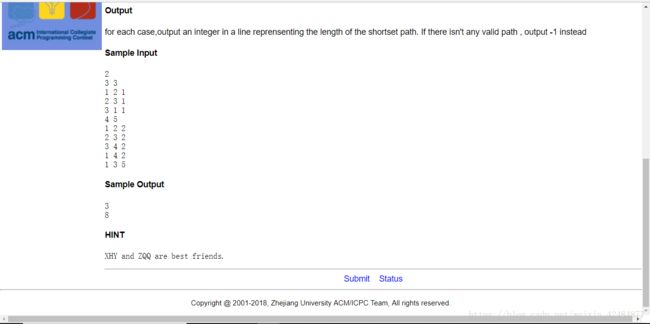
ACM出题日记
7.25
算是正经的出(ban)了一道题。
类似的思路我也想过,然后yjq学长刚好出了一道更难写的题,就直接搬过来了。
题目思路很巧妙,就是具体实现细节过于复杂,所以只能算半道好题。
考场上也没有人过。()有个学军的同学交了以前的标程都没过。)是有点遗憾。
算是积累了一次宝贵的出题经验。以后做的题多了,自己再多思考,就可以出出来更多好题了。原创题还是一个很重要的能力!
造数据也是非常重要的,一道好题一定要配上很强的数据。随机数据不强。一开始我用随机数据对拍,std犯了很大的错误都没有拍出来。还是yjq的数据靠谱!
#include" "<1,tot) cout<" "<" "<" "<" "<void init(){
rep(i,1,tot) adde(pnt[i],i) , jump[0][i] = pnt[i];
dfs(0);
rep(i,1,18)
rep(j,1,tot)
jump[i][j] = jump[i - 1][jump[i - 1][j]];
}
ll query(int x,int l,int r,int L,int R){ //查询和,注意合并的时候要把左右区间的相邻位置的和更新一下
if ( L > R ) return 0;
if ( !x ) return 0;
if ( L <= l && R >= r ) return sum[x] - sum2[x];
ll res = 0; int mid = (l + r) >> 1;
if ( L <= mid ) res += query(ls[x],l,mid,L,R);
if ( R > mid ) res += query(rs[x],mid + 1,r,L,R);
if ( L <= rm[ls[x]] && lm[rs[x]] <= R ) res -= (ll)rm[ls[x]] * lm[rs[x]];
return res;
}
int queryL(int x,int l,int r,int d){ //查询一个位置的前驱
if ( d < 1 ) return 0;
if ( !x ) return 0;
if ( l == r ) return l;
int mid = (l + r) >> 1;
if ( d <= mid || !rs[x] ) return queryL(ls[x],l,mid,d);
int id = queryL(rs[x],mid + 1,r,d);
if ( !id ) return rm[ls[x]];
return id;
}
int queryR(int x,int l,int r,int d){ //查询一个位置的后继
if ( d > n ) return 0;
if ( !x ) return 0;
if ( l == r ) return l;
int mid = (l + r) >> 1;
if ( d > mid || !ls[x] ) return queryR(rs[x],mid + 1,r,d);
int id = queryR(ls[x],l,mid,d);
if ( !id ) return lm[rs[x]];
return id;
}
ll query(int x,int len){ //统计不合法情况
int l = rm[x] - len + 1 , r = min(lm[x] + len - 2,n);
if ( rm[x] == lm[x] ){ //如果只有一个位置
return (ll)(len - 1) * (2 * n - len - 2) / 2;
}
//两个位置且互不相交
if ( queryR(x,1,n,lm[x] + 1) == rm[x] && rm[x] - lm[x] >= len ) return (ll)(len - 1) * (len - 1);
int fir = queryL(x,1,n,l - 1);
int last = queryR(x,1,n,r + 1);
ll csum = 0;
//如果没有相交的部分直接返回0
if ( last && last <= fir ) return 0;
// cout<
if ( !fir ) fir = len , csum = query(x,1,n,l,r) - (ll)lm[x] * len;
else csum = query(x,1,n,fir,r) - (ll)fir * fir; //要把上一个位置的贡献减掉
if ( last ){ //判一下最后一个合法位置是否是最后一次在原串中出现的位置
int rid = queryL(x,1,n,last - 1);
csum -= (ll)(rm[x] - len + 1) * (r - fir + 1);
csum += (ll)(r - rid + 1) * last;
}
else{
//按照推的式子算贡献,后面是个等差数列求和
csum -= (ll)(rm[x] - len + 1) * (rm[x] - fir);
csum += max(0ll,(ll)(lm[x] - rm[x] + len - 1) * (2 * n - lm[x] - rm[x] + len - 2) / 2);
}
return csum;
}
void solve(int l,int r){
int cur = rec[r],len = r - l + 1;
repd(i,18,0) if ( val[jump[i][cur]] >= len ) cur = jump[i][cur]; //倍增定位一个串对应的节点
ll ans = (ll)(n - 2) * (n - 1) / 2 - query(rt[cur],len);
printf("%lld\n",ans);
}
}sam;
int main(){
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
scanf("%d",&T);
// T = 1;
while ( T-- ){
sam.clear();
scanf("%d %d",&n,&q);
scanf("%s",ch + 1);
rep(i,1,n) sam.insert(ch[i] - '0');
sam.init();//sam.print();
while ( q-- ){
int l,r;
scanf("%d %d",&l,&r);
sam.solve(l,r);
}
}
return 0;
}
怎么上传题解啊QAQ
大概就是维护每个串的所有出现位置(pnt树上合并线段树)
然后计算一下贡献。细节非常多(见7.22文件夹)
附上第一场搬的sb题留作纪(jing)念(xing)
数据要认真造