机器学习（回归四）——线性回归-正则化

上篇博客是针对普通线性回归往往存在欠拟合的情况，采用多项式扩展的方式，从而映射到多维空间来拟合。多项式扩展的时候，如果指定的阶数比较大，那么有可能导致过拟合。也就是模型太契合训练数据了。数据上表现就是参数过多、过大。过拟合在实际机器学习应用中是普遍存在的。

正则化的引入

对于前面提到的目标函数：
$$J(\theta )=\frac{1}{2}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$
现在，我们要防止过拟合，可以通过调节参数值，让参数越小越好。也可以说参数越小，模型越简单。比如说除了两个参数外，其他的参数都小到为0了，此时完全可以只关心这两个参数的情况了，从而从高维空间降到了低维空间。

为了防止数据过拟合，也就是的θ值在样本空间中不能过大/过小，可以在目标函数之上增加一个平方和损失：
$$J(\theta )=\frac{1}{2}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2+\lambda \sum _{i=1}^m{\mathbf{\theta }}_j^2$$
加上的这项后半部分，也可写成 ${\theta }^T\theta$ 或 ||θ||（也叫二范式）这就是正则项：$\lambda {\sum }_{i=1}^m{\mathbf{\theta }}_j^2$ 这里这个正则项叫做 L2-norm，有的地方也叫惩罚项，就是原始J(θ)的一个惩罚值。

两部分加在一起最小化，是我们要达到的目的。第一项是凸函数，第二项也是凸函数，而且是两个开口向上的凸的函数，叠加后还是凸函数。也就存在最小值，且在极值的位置，即求导为0的地方。最终求得的结果：
$$\mathbf{\theta }={\left(X^{T}X+\lambda I\right)}^{-1}{X}^T\mathbf{y}$$

是不是很熟悉？没错这就是《机器学习（回归一）——线性回归-最小二乘》中为了防止不可逆或者过拟合的问题存在，可以增加额外数据影响，使得最终的矩阵是可逆的，从而得到的式子。

常见线性回归正则化模型

故：为了解决过拟合问题，我们可以选择在损失函数中加入惩罚项（对于系统过磊的惩罚），主要分为L1-norm和L2-norm，以及他俩结合的线性回归模型：

1. 使用L2正则的线性回归模型就称为Ridge回归（岭回归）
   $$J(\theta )=\frac{1}{2}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2+\lambda \sum _{i=1}^m{\mathbf{\theta }}_j^2\lambda >0$$
2. 使用L1正则的线性回归模型就称为LASSO回归（Least Absolute Shrinkage and Selection Operator）
   $$J(\theta )=\frac{1}{2}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2+\lambda \sum _{i=1}^m|{\mathbf{\theta }}_j|\lambda >0$$
3. 同时使用L1正则和L2正则的线性回归模型就称为 Elasitc Net 算法（弹性网络算法）
   $$J(\theta )=\frac{1}{2}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2+\lambda \left(p\sum _{i=1}^m|{\mathbf{\theta }}_j|+(1-p)\sum _{i=1}^m{\mathbf{\theta }}_j^2\right)\{\begin{array}{l}\lambda >0\\ p\in [0,1]\end{array}$$

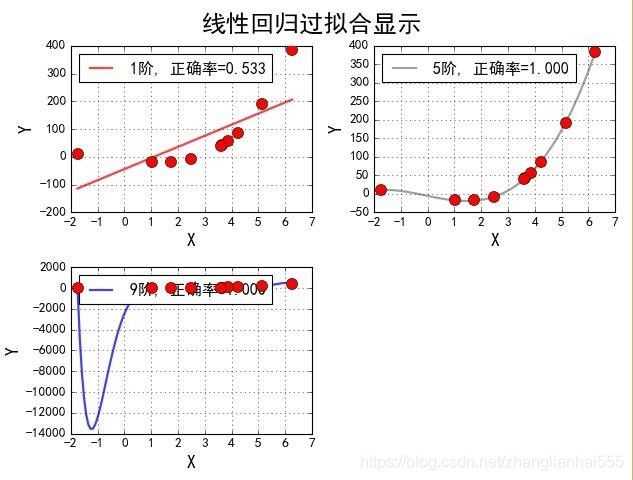
各种线性回归过拟合显示

这里自己手动生成数据，来看看各种不同的线性回归模型在过拟合时的显示效果。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import warnings
import sklearn
from sklearn.linear_model import LinearRegression, LassoCV, RidgeCV, ElasticNetCV
from sklearn.preprocessing import PolynomialFeatures#数据预处理，标准化
from sklearn.pipeline import Pipeline
from sklearn.linear_model.coordinate_descent import ConvergenceWarning

## 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
## 拦截异常
warnings.filterwarnings(action = 'ignore', category=ConvergenceWarning)

## 创建模拟数据
np.random.seed(100)
np.set_printoptions(linewidth=1000, suppress=True)#显示方式设置，每行的字符数用于插入换行符，是否使用科学计数法
N = 10
x = np.linspace(0, 6, N) + np.random.randn(N)
y = 1.8*x**3 + x**2 - 14*x - 7 + np.random.randn(N)
## 将其设置为矩阵
x.shape = -1, 1
y.shape = -1, 1

## RidgeCV和Ridge的区别是：前者可以进行交叉验证
models = [
    Pipeline([
            ('Poly', PolynomialFeatures(include_bias=False)),
            ('Linear', LinearRegression(fit_intercept=False))
        ]),
    Pipeline([
            ('Poly', PolynomialFeatures(include_bias=False)),
            # alpha给定的是Ridge算法中，L2正则项的权重值，也就是ppt中的兰姆达
            # alphas是给定CV交叉验证过程中，Ridge算法的alpha参数值的取值的范围
            ('Linear', RidgeCV(alphas=np.logspace(-3,2,50), fit_intercept=False))
        ]),
    Pipeline([
            ('Poly', PolynomialFeatures(include_bias=False)),
            ('Linear', LassoCV(alphas=np.logspace(0,1,10), fit_intercept=False))
        ]),
    Pipeline([
            ('Poly', PolynomialFeatures(include_bias=False)),
            # la_ratio：给定EN算法中L1正则项在整个惩罚项中的比例，这里给定的是一个列表；
            # 表示的是在CV交叉验证的过程中，EN算法L1正则项的权重比例的可选值的范围
            ('Linear', ElasticNetCV(alphas=np.logspace(0,1,10), l1_ratio=[.1, .5, .7, .9, .95, 1], fit_intercept=False))
        ])
]

## 线性模型过拟合图形识别
plt.figure(facecolor='w')
degree = np.arange(1,N,4) # 阶
dm = degree.size
colors = [] # 颜色
for c in np.linspace(16711680, 255, dm):
    colors.append('#%06x' % int(c))

model = models[0]
for i,d in enumerate(degree):
    plt.subplot(int(np.ceil(dm/2.0)),2,i+1)
    plt.plot(x, y, 'ro', ms=10, zorder=N)

    # 设置阶数
    model.set_params(Poly__degree=d)
    # 模型训练
    model.fit(x, y.ravel())
    
    lin = model.get_params('Linear')['Linear']
    output = u'%d阶，系数为：' % (d)
    # 判断lin对象中是否有对应的属性
    if hasattr(lin, 'alpha_'):
        idx = output.find(u'系数')
        output = output[:idx] + (u'alpha=%.6f, ' % lin.alpha_) + output[idx:]
    if hasattr(lin, 'l1_ratio_'):
        idx = output.find(u'系数')
        output = output[:idx] + (u'l1_ratio=%.6f, ' % lin.l1_ratio_) + output[idx:]
    print (output, lin.coef_.ravel())
    
    x_hat = np.linspace(x.min(), x.max(), num=100) ## 产生模拟数据
    x_hat.shape = -1,1
    y_hat = model.predict(x_hat)
    s = model.score(x, y)
    
    z = N - 1 if (d == 2) else 0
    label = u'%d阶, 正确率=%.3f' % (d,s)
    plt.plot(x_hat, y_hat, color=colors[i], lw=2, alpha=0.75, label=label, zorder=z)
    
    plt.legend(loc = 'upper left')
    plt.grid(True)
    plt.xlabel('X', fontsize=16)
    plt.ylabel('Y', fontsize=16)

plt.tight_layout(1, rect=(0,0,1,0.95))
plt.suptitle(u'线性回归过拟合显示', fontsize=22)
plt.show()

看一下不同阶数时的参数及效果图：

1阶，系数为： [30.38156963]
5阶，系数为： [-19.20808111 -0.21353395 3.43106275 -0.38668311 0.02765531]
9阶，系数为： [-109.41783246 187.72709809 -113.70069709 -4.58285729 36.05537154 -17.39656084 3.82839962 -0.4129825 0.01765462]

## 线性回归、Lasso回归、Ridge回归、ElasticNet比较
plt.figure(facecolor='w')
degree = np.arange(1,N, 2) # 阶， 多项式扩展允许给定的阶数
dm = degree.size
colors = [] # 颜色
for c in np.linspace(16711680, 255, dm):
    colors.append('#%06x' % int(c))
titles = [u'线性回归', u'Ridge回归', u'Lasso回归', u'ElasticNet']

for t in range(4):
    model = models[t]#选择了模型--具体的pipeline(线性、Lasso、Ridge、EN)
    plt.subplot(2,2,t+1) # 选择具体的子图
    plt.plot(x, y, 'ro', ms=10, zorder=N) # 在子图中画原始数据点； zorder：图像显示在第几层

    # 遍历不同的多项式的阶，看不同阶的情况下，模型的效果
    for i,d in enumerate(degree):
        # 设置阶数(多项式)
        model.set_params(Poly__degree=d)
        # 模型训练
        model.fit(x, y.ravel())

        # 获取得到具体的算法模型
        # model.get_params()方法返回的其实是一个dict对象，后面的Linear其实是dict对应的key
        # 也是我们在定义Pipeline的时候给定的一个名称值
        lin = model.get_params()['Linear']
        # 打印数据
        output = u'%s:%d阶，系数为：' % (titles[t],d)
        # 判断lin对象中是否有对应的属性
        if hasattr(lin, 'alpha_'): # 判断lin这个模型中是否有alpha_这个属性
            idx = output.find(u'系数')
            output = output[:idx] + (u'alpha=%.6f, ' % lin.alpha_) + output[idx:]
        if hasattr(lin, 'l1_ratio_'): # 判断lin这个模型中是否有l1_ratio_这个属性
            idx = output.find(u'系数')
            output = output[:idx] + (u'l1_ratio=%.6f, ' % lin.l1_ratio_) + output[idx:]
        # line.coef_：获取线性模型的参数列表，也就是我们ppt中的theta值，ravel()将结果转换为1维数据
        print (output, lin.coef_.ravel())

        # 产生模拟数据
        x_hat = np.linspace(x.min(), x.max(), num=100) ## 产生模拟数据
        x_hat.shape = -1,1
        # 数据预测
        y_hat = model.predict(x_hat)
        # 计算准确率
        s = model.score(x, y)

        # 当d等于5的时候，设置为N-1层，其它设置0层；将d=5的这条线凸显出来
        z = N + 1 if (d == 5) else 0
        label = u'%d阶, 正确率=%.3f' % (d,s)
        plt.plot(x_hat, y_hat, color=colors[i], lw=2, alpha=0.75, label=label, zorder=z)
    
    plt.legend(loc = 'upper left')
    plt.grid(True)
    plt.title(titles[t])
    plt.xlabel('X', fontsize=16)
    plt.ylabel('Y', fontsize=16)
plt.tight_layout(1, rect=(0,0,1,0.95))
plt.suptitle(u'各种不同线性回归过拟合显示', fontsize=22)
plt.show()

代码看着挺多，其实主要是画图。再看一下运行效果及参数：


发现：到三阶的时候，都拟合的特别好，但是到九阶时，普通的线性回归，出了明显的拐线。普通回归，到9阶时，有多个比较大的系数，而其他的没有出现这个情况；Lasso在高阶时，出现了好多非常接近0的系数。

L1正则与L2正则对比

• L2-norm中，由于对于各个维度的参数缩放是在一个圆内缩放的，不可能导致有维度参数变为0的情况，那么也就不会产生稀疏解；实际应用中，数据的维度中是存在噪音和冗余的，稀疏的解可以找到有用的维度并且减少冗余，提高回归预测的准确性和鲁棒性（减少了overfitting）(L1-norm可以达到最终解的稀疏性的要求)；

• Ridge模型具有较高的准确性、鲁棒性以及稳定性；LASSO模型具有较高的求解速度。（等于0的参数，我们就可以不用考虑，这个过程叫特征选择）；

• 如果既要考虑稳定性也考虑求解的速度，就使用Elasitc Net。

以两个参数为例，第一二个参数分别为横纵坐标，到原点小于等t的图形，分别是两个阴影部分。（左图是L1，右图是L2）J(θ)类似于一个椭圆（ax² + by²=c）。
在上图中就是一圈的椭圆线，等高线，椭圆上的值是相等的。中间的那个点是最优的解。
加上惩罚项过，最优，就是交点处。图1，交点，可以在坐标轴上，即参数可能出现0的情况。但图2就不行。

总结：

普通的线性回归往往拟合效果不好，比如图形是曲线的形式，可以做一个多项式扩展，变到高维空间。也可以说多项式扩展能解决线性回归模型欠拟合的情况。但多项式的阶数如果太高，就会导致过拟合的情况，也就是训练集上特别好，测试集不太理想。

对于过拟合可以使用L1或L2来解决，也就是在J(θ) 的基础上把模型的复杂度加上，如岭回归。

在线性回归中，可以理解为就是θ值，我们把θ值加上去，但值有正有负所以出现了常用的两种形式：L1 L2，并引入超参λ来进行调整