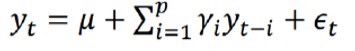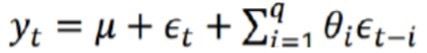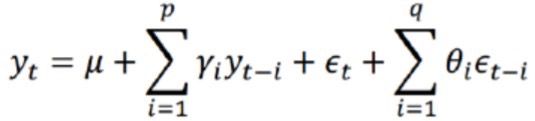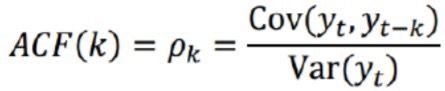使用ARIMA进行股票预测

一、ARIMA介绍

1、简介

        ARIMA模型的全称叫做自回归移动平均模型，全称是(ARIMA, Autoregressive Integrated Moving Average Model)。是统计模型(statistic model)中最常见的一种用来进行时间序列 预测的模型。模型十分简单，只需要内生变量而不需要借助其他外生变量。

2、模型介绍

1.自回归模型(AR)

        描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求，p阶自回归过程的公式定义为：

是当前值，是常数项，P是阶数，是自相关系数，是误差。不过要想使用自回归模型，有如下一些限制：

• 自回归模型是用自身的数据来进行预测；
• 必须具有平稳性；
• 必须具有自相关性，如果自相关系数(φi)小于0.5，则不宜采用；
• 自回归只适用于预测与自身前期相关的现象。

2.移动平均模型(MA)

        移动平均模型关注的是自回归模型中的误差项的累加，q阶自回归过程的公式定义：

移动平均法能有效地消除预测中的随机波动。

3.自回归移动平均模型(ARMA)

        ARIMA(p,d,q)模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)。其实就是，自回归与移动平均的结合。

        ARIMA模型干的事情就是：将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。公式定义为：

AR是自回归，p为自回归项，MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。

3、自相关函数

1.自相关函数ACF

        有序的随机变量序列与其自身相比较，自相关函数反映了同一序列在不同时序的取值之间的相关性。公式表示：

Pk的取值范围为[-1,1]。

2.偏自相关函数(PACF)

        对于一个平稳AR(p)模型，求出滞后k自相关系数p(k)时，实际上得到并不是x(t)与x(t-k)之间单纯的相关关系。x(t)同时还会受到中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的影响，而这k-1个随机变量又都和x(t-k)具有相关关系，所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响。

        也就是说，ACF还包含了其他变量的影响，而偏自相关系数PACF是严格这两个变量之间的相关性。PACF剔除了中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的干扰之后，x(t-k)对x(t)影响的相关程度。

二、数据获取

        股票数据采用的是雅虎财经提供的API接口（pandas-datareader），导包如下：

%matplotlib inline
import pandas as pd
import pandas_datareader
import datetime
import matplotlib.pylab as plt
import seaborn as sns
from matplotlib.pylab import style
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt

#设置字体、图形样式
%config InlineBackend.figure_format = 'retina'
sns.set_style("whitegrid")
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False

%matplotlib inline

plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']

我这里获取的是太极实业的股票数据，股票代码为600667.SS，数据时间段为2019到现在的数据

start = pd.datetime(2019, 1, 1)
end = pd.datetime.today()
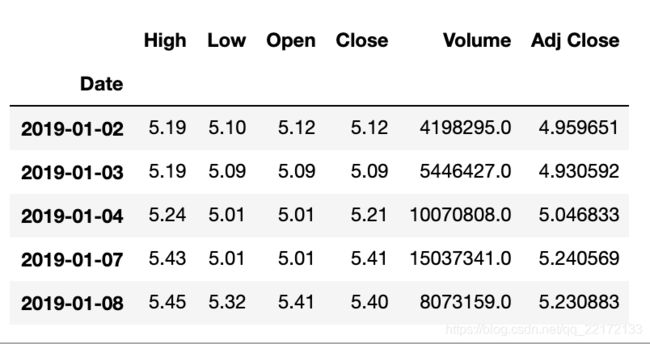
stock = pandas_datareader.DataReader('600667.SS', 'yahoo', start, end)
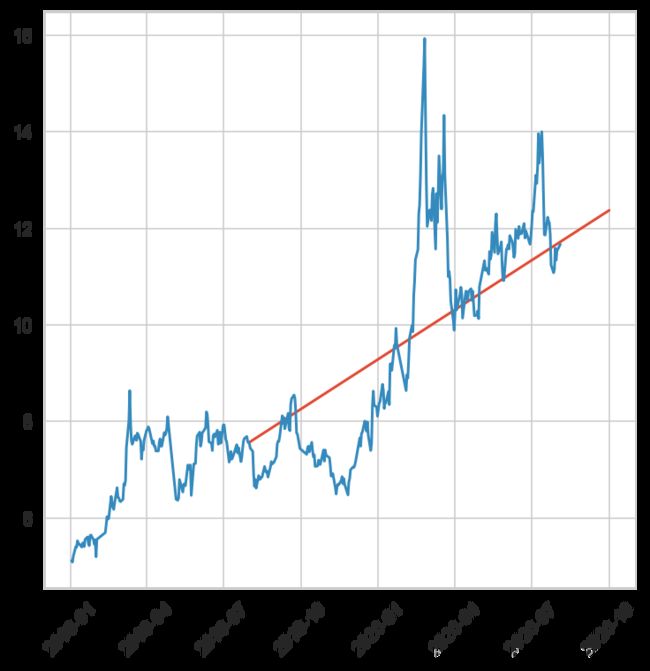
stock.head()

其中Close就是当日净值，先看一下数据走势，

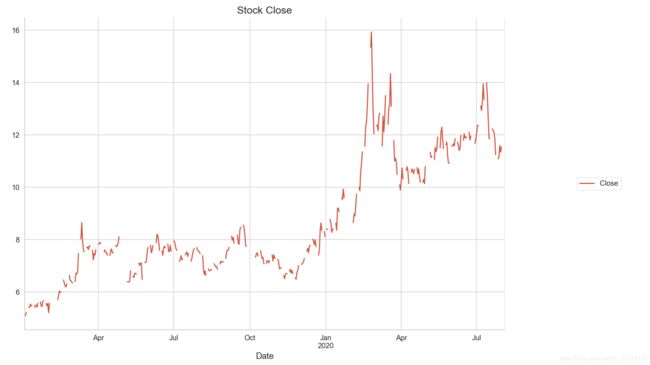
stock_train.plot(figsize=(12,8))
plt.legend(bbox_to_anchor=(1.25, 0.5))
plt.title("Stock Close")
sns.despine()

这里以天为单位，把缺失数据（休市）填充上，我这里填充的线性取值

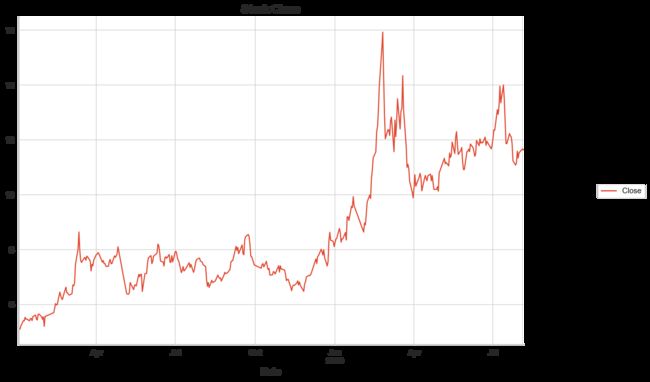
stock_train = stock_train.resample('D').interpolate('linear')

stock_train.plot(figsize=(12,8))
plt.legend(bbox_to_anchor=(1.25, 0.5))
plt.title("Stock Close")
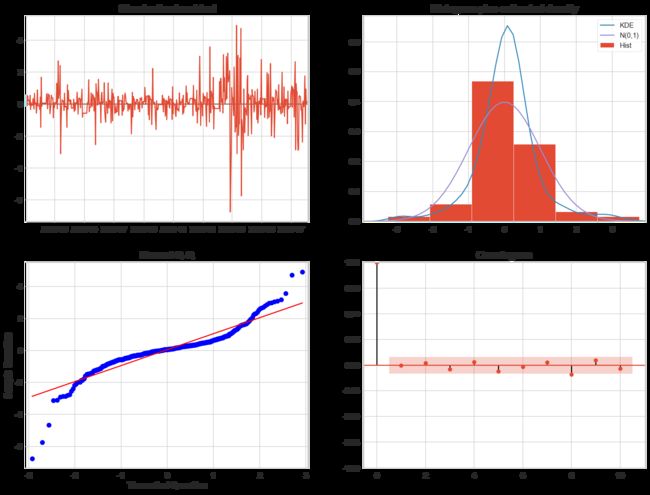
sns.despine()

 我们要想深入的了解数据，再直观一些，

def tsplot(y, lags=None, title='', figsize=(14, 8)):
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    hist_ax = plt.subplot2grid(layout, (0, 1))
    
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y.plot(ax=hist_ax, kind='hist', bins=25)
    hist_ax.set_title('Histogram')
    sns.despine()
    plt.tight_layout()
    return ts_ax, acf_ax, pacf_ax

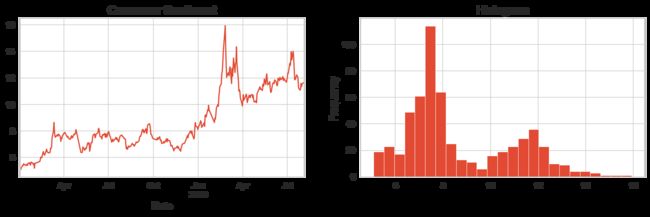
tsplot(stock_train, title='Consumer Sentiment', lags=36)

三、数据预处理

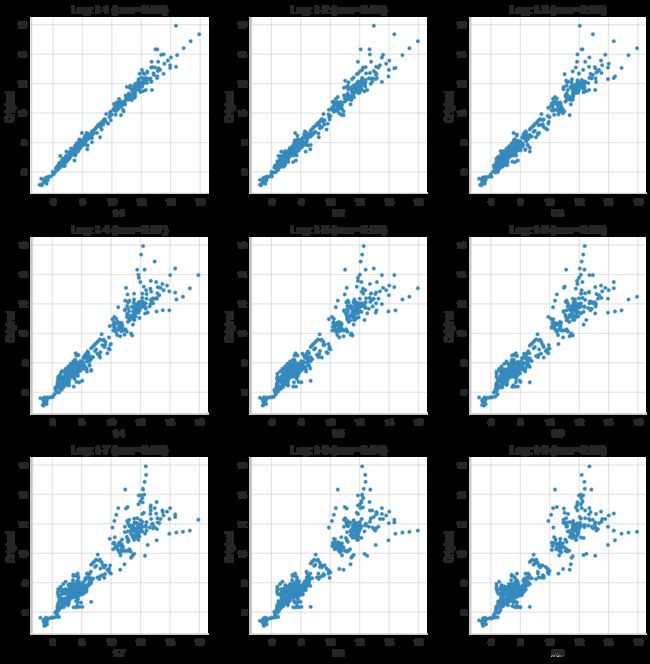
        根据上面的数据展示，可以看出数据分布不太稳定，即不平滑，做一下差分处理，可以把各阶差分数据画成散点图表示出来，如下：

lags=9
ncols=3
nrows=int(np.ceil(lags/ncols))

fig, axes = plt.subplots(ncols=ncols, nrows=nrows, figsize=(4*ncols, 4*nrows))

for ax, lag in zip(axes.flat, np.arange(1,lags+1, 1)):
    lag_str = 't-{}'.format(lag)
    X = (pd.concat([stock_train, stock_train.shift(-lag)], axis=1,
                   keys=['y'] + [lag_str]).dropna())

    X.plot(ax=ax, kind='scatter', y='y', x=lag_str);
    corr = X.corr().as_matrix()[0][1]
    ax.set_ylabel('Original')
    ax.set_title('Lag: {} (corr={:.2f})'.format(lag_str, corr));
    ax.set_aspect('equal');
    sns.despine();

fig.tight_layout();

根据散点图知道一阶差分即可（在一条直线上）。

stock_diff = stock_train.diff()
stock_diff = stock_diff.dropna()

plt.figure()
plt.plot(stock_diff)
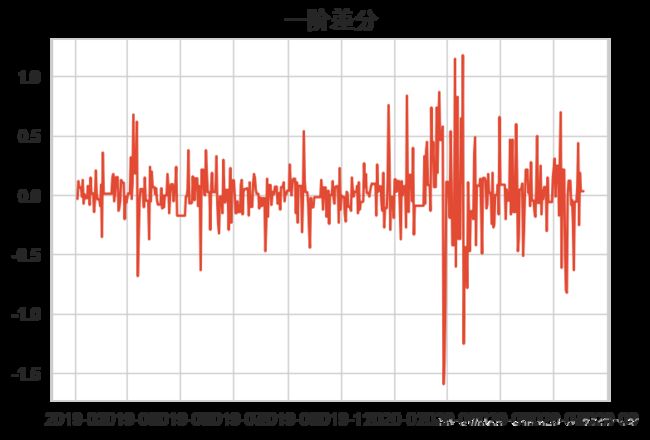
plt.title('一阶差分')
plt.show()

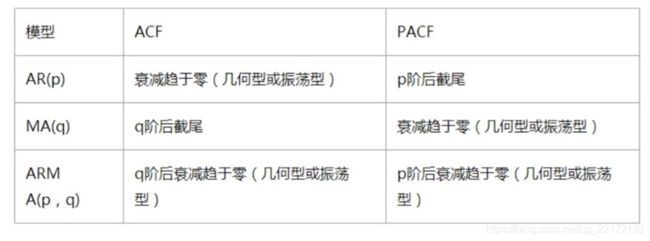
基本还算平稳，2～3月份数据波动大，因为疫情原因，可以把这部分数据去除掉比较好，不过这里就不去了。前面在介绍ARMA模型的时候，有说明过p，q，d这几个参数，d显然这里取1。那么p，q怎么确定呢？要根据ACF和PACF来确定，具体规则如下：

截尾，落在置信区间内，95%的点都符合该规则。我们需要先绘制acf和pacf的图，

fig = plt.figure(figsize=(12,8))

ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(stock_diff, lags=20,ax=ax1)
ax1.xaxis.set_ticks_position('bottom')
fig.tight_layout();

ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(stock_diff, lags=20, ax=ax2)
ax2.xaxis.set_ticks_position('bottom')
fig.tight_layout();

根据上面的规则，首先来确定q的阶数，看acf图，阴影部分表示截尾部分，也就是看从几阶开始进入阴影，从图上可以看出来是2阶，并且此时pacf也趋近于零了。再来确定p的阶数，看pacf图，可以看出2阶以后就满足了，此时acf也是趋近于0。

四、模型训练

model = ARIMA(stock_train, order=(2, 1, 2),freq='D') # p,d,q
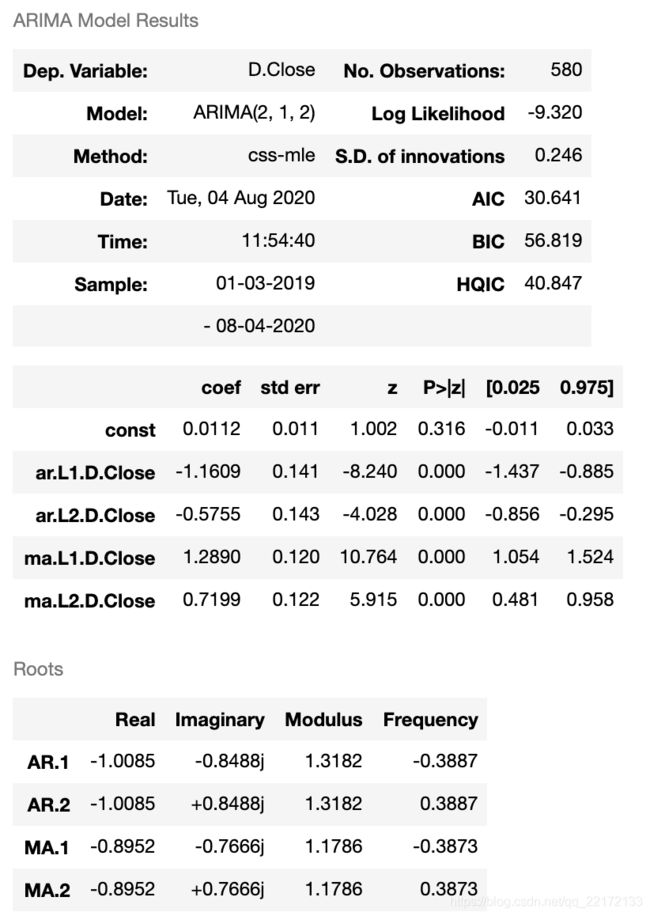
result = model.fit()
result.summary()

下面用训练的模型预测2019-08-01～2020-10-01的走势：

pred = result.predict('20190801', '20201001',dynamic=True, typ='levels')
plt.figure(figsize=(6, 6))
plt.xticks(rotation=45)
plt.plot(pred)
plt.plot(stock_train)

蓝线为实际值，红线为预测值，貌似没什么用。最后看一下，预测值的分布情况：

ARIMA本质上只能捕捉线性关系，而不能捕捉非线性关系。也就是说，采用ARIMA模型预测时序数据，必须是平稳的，如果不平稳的数据，是无法捕捉到规律的。股票数据是非稳定的，常常受政策和新闻的影响而波动，所以效果不佳，用一些谷歌搜索词变化提取一些特征，然后采用树模型预测可能会好点，以后有时间再试吧。