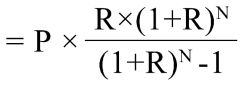非线性方程组求解-MatLab
一、非线性方程求根
通过以下问题学习此知识点:
现在你想买一套300万元的房子,首付40%,贷款20年,等额本息,已知月还款额为1.2万元,求贷款月利率为多少?
(1) 编写结合牛顿下山法和割线法的综合迭代方法求解函数,调用后求解;
(2) 使用steffenson法求解。
1、牛顿迭代法
-
又称为牛顿-拉弗森方法(Newton-Raphson method),单变量下又称为切线法。它是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。用牛顿迭代法解非线性方程,是把非线性方程f(x) = 0线性化的一种近似方法。
-
牛顿迭代法的本质是一种线性化方法,其基本思想是将非线性方程f(x)=0逐步归结为某种线性方程来求解。
设方程f(x)=0有近似根,将函数f(x)在点处展开,则有
于是,方程f(x)=0就可以近似表示为
对该方程求解,得到
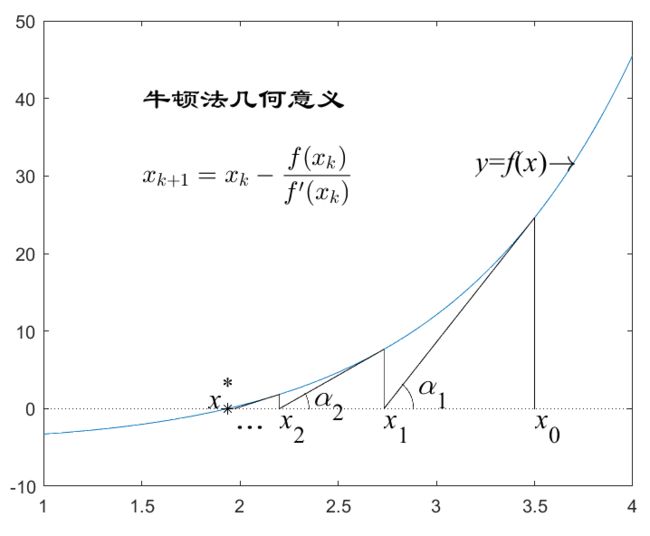
x k + 1 = x k − f ( x k ) f ′ ( x k ) ( k = 0 , 1 , 2 , 3... ) x_{k+1}=x_k-\frac{f(x_k)}{f^{'}(x_k)} \quad\quad (k=0,1,2,3...) xk+1=xk−f′(xk)f(xk)(k=0,1,2,3...)
该迭代公式即为 牛顿迭代公式。
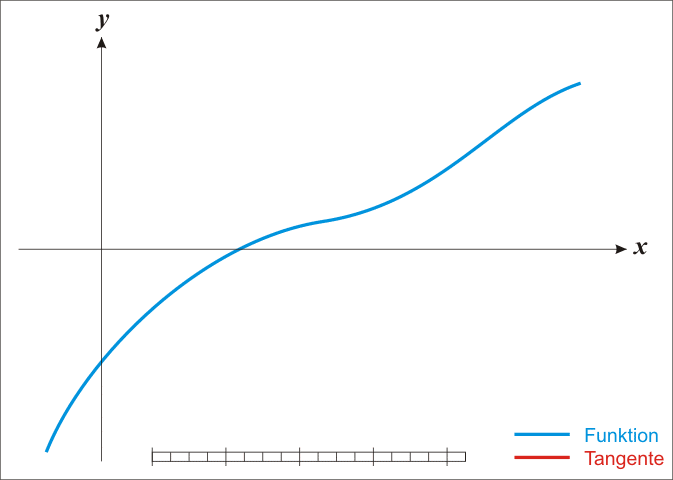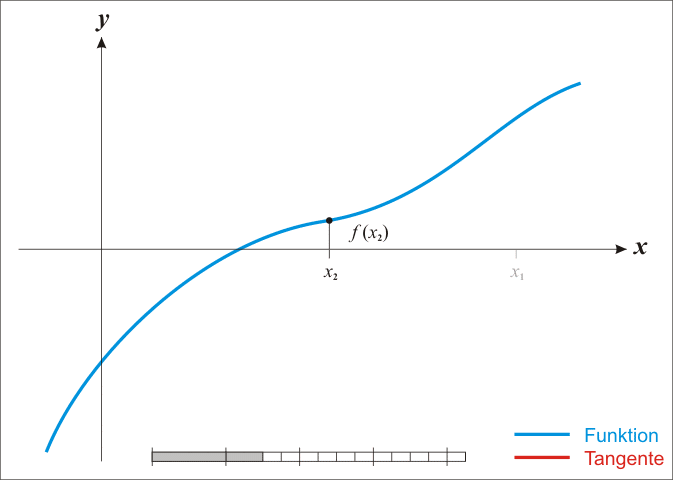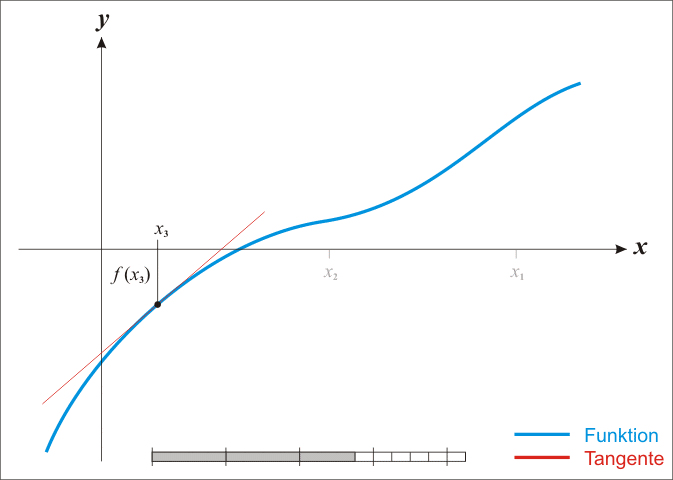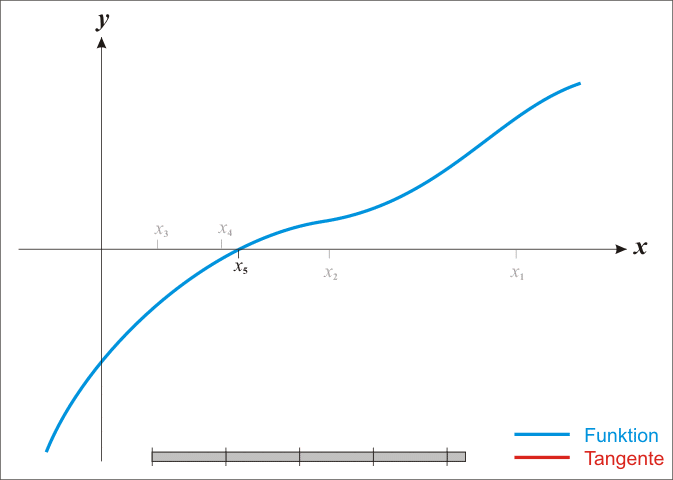
x k + 1 x_{k+1} xk+1是 y = f ( x ) y=f(x) y=f(x)的切线在点 ( x k , f ( x k ) ) (x_k,f(x_k)) (xk,f(xk))处与 x x x轴交点的横坐标。
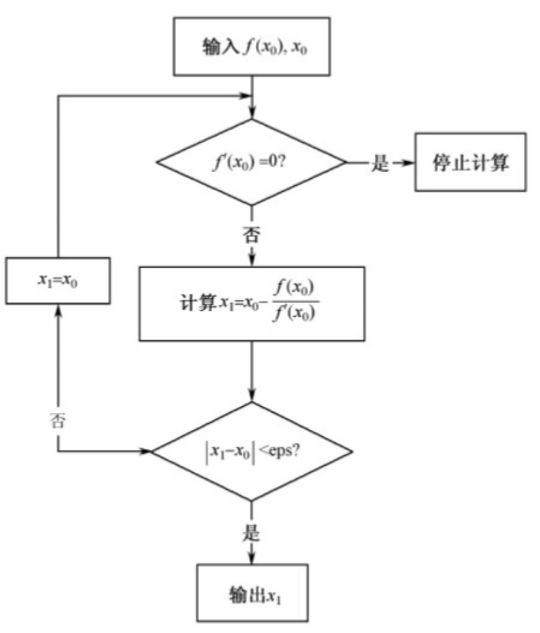
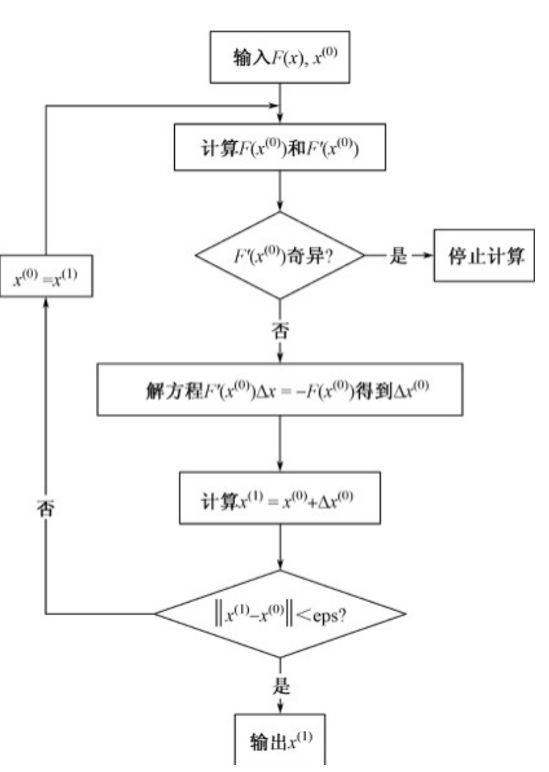
算法流程图:
对牛顿迭代法更加直观的理解
2、牛顿下山法
在牛顿迭代法中,有时候会出现如下迭代回退的情况,导致出现死循环
当选取初值有困难时,可改用如下迭代格式,以扩大初值的选取范围,
x n + 1 = x n − λ f ( x k ) f ′ ( x k ) x_{n+1}=x_n-\lambda\frac{f(x_k)}{f^{'}(x_k)} xn+1=xn−λf′(xk)f(xk)
其中λ称为下山因子,λ选取应满足单调性条件
∣ f ( x n + 1 ∣ < ∣ f ( x n ) ∣ |f(x_{n+1}|<|f(x_n)| ∣f(xn+1∣<∣f(xn)∣
这样的算法称下山法.将下山法和牛顿法结合起来使用的方法,称为牛顿下山法.
下山因子λ的选择是逐步探索的过程.从λ=1开始反复将λ减半进行试算,如果能定出λ使单调性条件成立则“下山成功”.与此相反,如果找不到使单调性条件成立的λ,则“下山失败”.此时需另选初值x0重算
3、割线法引入
割线法又称为弦截法法
-
为什么要引入割线法?
在牛顿下山法中我们需要计算被切割点的倒数,在多次迭代情况下,调用MatLab自带的求导函数会占用很多计算资源,所以,我们采用向后有限差分来近似导数计算,什么意思?
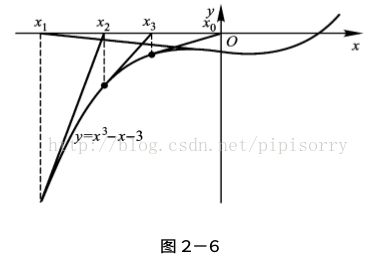
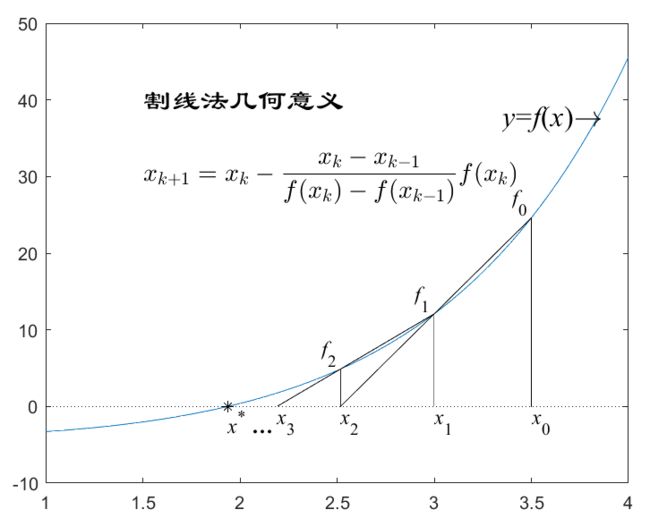
上图:
在割线法中,省略了求导步骤,用 x k x_k xk和 x k − 1 x_{k-1} xk−1两点连成的直线与x轴的交点近似代替了牛顿法中 x k + 1 x_{k+1} xk+1的求解
由此,减少了计算资源的消耗
-
需要注意
弦截法和牛顿迭代法都是线性化方法,牛顿迭代法在计算 x n + 1 x_{n+1} xn+1时只用到前一步的值 x n x_n xn,而弦截法用到前面两步的结果 x n x_n xn和 x n + 1 x_{n+1} xn+1,因此使用割线法必须先给出两个初值值 x 0 , x 1 x_0,x_{1} x0,x1.
牛顿下山法和割线法结合算法如下:
function [x,iter,X]=newton_secant(fun,x0,x1,eps,maxiter)
% 牛顿下山+割线法求解非线性方程的根
% 输入参数:
% ---fun:迭代函数
% ---x0,x1:初始迭代点
% ---eps:精度要求,默认值为1e-6
% ---maxiter:最大迭代次数,默认值为1e4
% 输出参数:
% ---x:非线性方程的近似根
% ---iter:迭代次数
% ---X:每一步迭代的结果
if nargin<3,error('输入参数至少需要3个!'),end
if nargin<4|isempty(eps),eps=1e-6;end
if nargin<5|isempty(maxiter),maxiter=1e4;end
f0 = feval(fun,x0); % 计算x0处的函数值
f1 = feval(fun,x1); % 计算x1处的函数值
k=0;err=1;%k统计迭代次数,err表示迭代精度
while abs(err)>eps
lambda=1;%下山因子
x2=x1-lambda*f1*(x1-x0)/(f1-f0);
f2 = feval(fun,x2);
while abs(f2)>=abs(f1)
lambda=lambda/2; % 更新lambda
x2=x1-lambda*f1*(x1-x0)/(f1-f0); % 牛顿下山迭代,割线法代替求导
f2=feval(fun,x2);
end
x0=x1;x1=x2;
f0=f1;f1=f2;
err=x1-x0;%更新迭代精度
k=k+1;
X(k)=x2;
end
if k>=maxiter
error('迭代次数超限,迭代失败!')
end
x=x2;iter=k;X=X';
end
解决第一个问题
180 × x ( 1 + x ) 240 ( 1 + x ) 240 − 1 − 1.2 = 0 180\times\frac{x(1+x)^{240}}{(1+x)^{240}-1}-1.2=0 180×(1+x)240−1x(1+x)240−1.2=0
fun=@(x)180*(x*(1+x)^240)/((1+x)^240-1)-1.2;
命令行调用函数解方程:
[x,iter,X]=newton_secant(fun,0.007,0.006)
输出:
x =
0.00426762528564472
iter =
4
X =
0.00437256674949125
0.0042721389151354
0.00426763795820826
0.00426762528564472
可以看到:
月利率约为 0.427 % 0.427\% 0.427%
4、steffenson法
Steffeson法的导数近似方法:
f ′ ( x k ) ≈ f ( x k + f ( x k ) ) − f ( x k ) f ( x k ) f^{'}(x_k)\approx\frac{f(x_k+f(x_k))-f(x_k)}{f(x_k)} f′(xk)≈f(xk)f(xk+f(xk))−f(xk)
则迭代公式为:
x k + 1 = x k − f 2 ( x k ) f ( x k + f ( x k ) ) − f ( x k ) ( k = 1 , 2 , 3... ) x_{k+1}=x_k-\frac{f^{2}(x_k)}{f(x_k+f(x_k))-f(x_k)}\quad\quad (k=1,2,3...) xk+1=xk−f(xk+f(xk))−f(xk)f2(xk)(k=1,2,3...)
废话少说,上代码:
function [x,iter,X] = steffenson(fun,x0,eps,maxiter)
% Steffenson法求解非线性方程的根
% 输入参数:
% ---fun:迭代函数
% ---x0:初始迭代点
% ---eps:精度要求,默认值为1e-6
% ---maxiter:最大迭代次数,默认值为1e4
% 输出参数:
% ---x:非线性方程的近似根
% ---iter:迭代次数
% ---X:每一步迭代的结果
if nargin<2,error('输入参数至少需要2个!'),end
if nargin<3|isempty(eps),eps=1e-6;end
if nargin<4|isempty(maxiter),maxiter=1e4;end
k=0;err=1;
while abs(err)>eps;
k=k+1;
f0 = feval(fun,x0); % 计算x0处的函数值
x1=x0-f0^2/(feval(fun,x0+f0)-f0); % Steffenson法迭代公式
err=x1-x0;
x0 = x1; % 更新x0数值
X(k)=x1;
end
x=x1;iter=k;X=X';
命令行调用函数解方程:
[x,iter,X]=steffenson(fun,0.007,0.006)
输出:
x =
0.00426762553393485
iter =
6
X =
0.005042607730931
0.0045032072675304
0.00433124100792348
0.00427709276934277
0.00426790263879553
0.00426762553393485
可以看到:
月利率约为 0.427 % 0.427\% 0.427%,但是迭代次数为6次
二、非线性方程组求解
通过以下问题学习此知识点:
用牛顿法求解二元方程组的根
x 2 c o s 2 x + y 2 s i n ( 2 y ) = 1 x 3 + y 3 − 6 c o s ( 2 x y ) = − 1 \begin{array}{cc} x^2 \mathrm{cos2x}+y^2 \mathrm{sin(2y)}=1 & \\ x^3 +y^3 -6\mathrm{cos(2xy)}=-1 & \end{array} x2cos2x+y2sin(2y)=1x3+y3−6cos(2xy)=−1
1、牛顿法解方程组
非线性方程组的求法有很多,此处仅对使用牛顿法求解非线性方程组的根进行学习。
将多元向量函数F(x) 在点处展开
F ( x ) ≈ F ( x ( k ) ) + F ′ ( x ( k ) ) ( x − x ( k ) ) ) F\left(x\right)\approx F\left(x^{\left(k\right)} \right)+F^{\prime } \left(\left.x^{\left(k\right)} \right)\left(x-x^{\left(k\right)} \right)\right) F(x)≈F(x(k))+F′(x(k))(x−x(k)))
其中,是F(x)的Jacobi矩阵
因此,可以得到求解非线性方程组的迭代方程
x ( k + 1 ) = x ( k ) − [ F ′ ( x ( k ) ) ] − 1 F ( x ( k ) ) x^{\left(k+1\right)} =x^{\left(k\right)} -{\left\lbrack F^{\prime } \left(x^{\left(k\right)} \right)\right\rbrack }^{-1} F\left(x^{\left(k\right)} \right) x(k+1)=x(k)−[F′(x(k))]−1F(x(k))
---------流程图--------
上代码:
function [x,iter,X]=newtong(fun,x0,eps,maxiter)
% Newton法求解非线性方程组的根
% 输入参数:
% ---fun:迭代函数
% ---x0:初始迭代点向量
% ---eps:精度要求,默认值为1e-6
% ---maxiter:最大迭代次数,默认值为1e4
% 输出参数:
% ---x:非线性方程的近似解向量
% ---iter:迭代次数
% ---X:每一步迭代的结果
if nargin<2,error('输入参数至少需要2个!'),end
if nargin<3|isempty(eps),eps=1e-6;end
if nargin<4|isempty(maxiter),maxiter=1e4;end
k=0;err=1;
while err>eps
k=k+1;
[fx0,J]=feval(fun,x0); % 求函数fun的值和jacobi矩阵
x1=x0-J\fx0; % 牛顿法迭代公式
err=norm(x1-x0);
x0=x1;
X(k,:)=x1;
end
if k==maxiter
error('迭代次数超限,迭代失败!')
end
x=x1;iter=k;
end
function [y,J]=fun(x)
% 非线性方程组
% 函数文件描述,返回函数值和jacobi矩阵
y=[x(1)^2*cos(2*x(1))+x(2)^2*sin(2*x(2))-1;
x(1)^3+x(2)^3-6*cos(2*x(1)*x(2))+1];
% 求Jacobi矩阵
syms xx yy; % 声明符号变量
%J=jacobian([2*xx-yy-exp(-xx);-xx+2*yy-exp(-yy)],[xx yy]); % 求符号jacobi矩阵
J = jacobian([xx^3*cos(2*xx)+yy^2*sin(2*yy)-1,xx^3+yy^3-6*cos(2*xx*yy)+1], [xx, yy]);
xx = x(1);
yy = x(2);
J=eval(J); % 替换
end
命令行输入:
[x,iter,X]=newtong(@fun,[5;2])
输出:
x =
16.0945044603024
-16.1035071010038
iter =
98
X =
5.10274043149926 -0.119124207216952
5.24942127220357 2.38096639162783
5.02977093770551 -13.5938666862748
16.0396552014422 -8.16234689739867
16.3648055755991 -18.4422298393681
16.5029906700455 -16.5584665672948
……