数理统计之参数估计与假设检验（一）——区间估计

参数估计与假设检验

区间估计

简单的区间估计就是对概率统计知识的应用。在浙江大学的概统书上将区间分布的几种情况进行了分类：

单个总体$N(\mu ,{\sigma }^2)$的情况

1、均值$\mu$的置信区间
（1）${\sigma }^2$已知；（2）${\sigma }^2$未知。
2、方差${\sigma }^2$的置信区间

两个总体$N({\mu }_1,{\sigma }_1^2),N({\mu }_2,{\sigma }_2^2)$的情况

1、两个总体均值差的置信区间；
2、两个总体方差比的置信区间。
具体的细节在这里就不一一赘述了。大家可以参考浙江大学的《概率论与数理统计》。

应用实例

下面大部分应用实例仅做方法和思路上的提示。

例题1：

方法一：公式法

在求得均值和方差之后，可以直接将公式转变成代码：

t=[mu-sig/sqrt(n)*tinv(1-alpha/2,n-1),mu+sig/sqrt(n)*tinv(1-alpha/2,n-1)];

方法二：直接通过MATLAB自带函数进行假设检验：

%% 以下命令ttest的返回值ci就直接给出了置信区间估计
% 其中data是要进行假设检验的数据集，要求是向量形式；mu是均值
[h,p,ci]=ttest(data,mu,0.05);  %通过假设检验也可求得置信区间

例题2：

该题目是针对于单侧的置信下限的求解

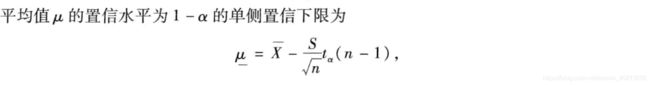
方法一：公式法
别忘了置信区间分布的计算和设定：

alpha=0.05; ta=tinv(1-alpha,4);

在求得了数据的均值和方差之后：

% 其中junzhi代表数据的均值
mu=junzhi-s/sqrt(n)*ta; %计算单侧置信下限

方法二：假设检验函数

% 其中data是原始数据集（注意要是向量的形式），junzhi代表原始数据集的均值
[h,p,ci]=ttest(data,junzhi,'Alpha',0.05,'Tail','right');  %通过假设检验也可求得置信区间

例题3：

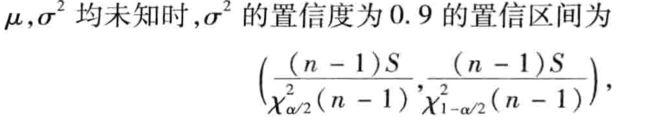
本题目在求解均值置信区间的基础上加入了方差的置信区间计算
当然本题目可以使用公式法计算，但是没有直接调用函数来得快。

clc, clear
x1=[6.683, 6.681, 6.676, 6.678, 6.679, 6.672];
x2=[6.661, 6.661, 6.667, 6.667, 6.664];
[h1,p1,ci1,st1]=ttest(x1,mean(x1),'Alpha',0.1); %均值检验和区间估计
[h2,p2,ci2,st2]=ttest(x2,mean(x2),'Alpha',0.1);
[h3,p3,ci3,st3]=vartest(x1,var(x1),'Alpha',0.1); %方差检验和区间估计
[h4,p4,ci4,st4]=vartest(x2,var(x1),'Alpha',0.1);

如果该问题将两个样本集合放在一起考虑，问题则进化成了求样本均值差的置信区间：

clc, clear
x1=[6.683, 6.681, 6.676, 6.678, 6.679, 6.672];
x2=[6.661, 6.661, 6.667, 6.667, 6.664];
[h,p,ci,st]=ttest2(x1,x2,'Alpha',0.1);

参考文献

司守奎，孙玺菁. 数学建模算法与应用. 北京：国防工业出版社，2011.