双数组字典树Double Array Trie（上）

本文转载自：http://www.cnblogs.com/zhangchaoyang 作者:Orisun 如有侵权，请联系本人，一定修改至您满意为止。

Trie树主要应用在信息检索领域，非常高效。今天我们讲Double Array Trie，请先把Trie树忘掉，把信息检索忘掉，我们来讲一个确定有限自动机（deterministic finite automaton ，DFA）的故事。所谓“确定有限自动机”是指给定一个状态和一个变量时，它能跳转到的下一个状态也就确定下来了，同时状态是有限的。请注意这里出现两个名词，一个是“状态”，一个是“变量”，下文会举例说明这两个名词的含义。

举个例子，假设我们一共有10个汉字，每个汉字就是一个“变量”。我们为每个汉字编个序号。

 

1	2	3	4	5	6	7	8	9	10
啊	阿	埃	根	胶	拉	及	廷	伯	人

             表1. “变量”的编号

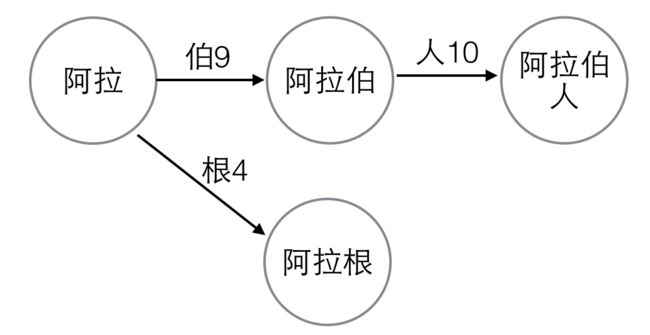
这10个汉字一共可以构成6个词语：啊，埃及，阿胶，阿根廷，阿拉伯，阿拉伯人。　　　　　　　　　

这里的每个词以及它的任意前缀都是一个“状态”，“状态”一共有10个：啊,阿,埃,阿根,阿根廷,阿胶,阿拉,阿拉伯,阿拉伯人,埃及

我们把DFA图画出来:

　　　　　　　　图1. DFA，同时也是Trie树

在图中每个节点代表一个“状态”，每条边代表一个“变量”，并且我们把变量的编号也标在了图中。

下面我们构造两个int数组：base和check，它们的长度始终是一样的。数组的长度定多少并没有严格的规定，反正随着词语的插入，数组肯定是要扩容的。说到数组扩容，大家可以看一下java中HashMap的扩容策略，每次扩容数组的长度都会变为2的整次幂。HashMap中有这么一个精妙的函数：

//给定一个整数，返回大于等于这个数的2的整次幂
static  int  tableSizeFor( int  cap) {
        int  n = cap -  1 ;
        n |= n >>>  1 ;
        n |= n >>>  2 ;
        n |= n >>>  4 ;
        n |= n >>>  8 ;
        n |= n >>>  16 ;
        return  (n <  0 ) ?  1  :  n +  1 ;
}

回到今天的正题，我们不妨把double array的初始长度就定得大一些。两数组元素初始值均为0。

double array的初始状态：

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
check	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
state

把词添加到词典的过程就给base和check数组中各元素赋值的过程。下面我们层次遍历图1所示的Trie树。

step1.

第一层上取到3个“状态”：啊,阿,埃。把这3个状态按照其对应的变量的编号（查表1）放到state数组中。

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
check	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
state	啊	阿	埃

step2.

当存在状态转移时，有

check[t]=s
base [s]+c=t

其中s和t代表某个状态在数组中的下标，c代表变量的编号。

此时层次遍历来到了图1所示DFA的第二层，我们看到“阿”的子节点有“阿根”、“阿胶”、“阿拉”，已知状态“阿”的下标是2，变量“根”、“胶”、“拉”的编号依次是4、5、6，下面我们要给base[2]赋值：从小到大遍历所有的正整数，直到发现某个数正整k满足base[k+4]=base[k+5]=base[k+6]=check[k+4]=check[k+5]=check[k+6]=0。得到k=1，那么就把1赋给base[2]，同时也确定了状态“阿根”、“阿胶”、“阿拉”的下标依次是k+4、k+5、k+6，即5、6、7，而且check[5]=check[6]=check[7]=2。

同理，“埃”的子节点是“埃及”，状态“埃”的下标是3，变量“及”的编号是7，此时有check[1+7]=base[1+7]=0，所以base[3]=1，状态“埃及”的下标是8，check[8]=3。

遍历完DFA的第二层后得到下表：

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
check	0	0	0	0	2	2	2	3	0	0	0	0	0	0	0	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及

step3.

重复step2，层次遍历完整查询树之后，得到：

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	0	1	1	0	1	0	1	0	0	1	0	0	0	0	0	0	0	0	0
check	0	0	0	0	2	2	2	3	5	7	10	0	0	0	0	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷	阿拉伯	阿拉伯人

step4.

最后遍历一次DFA，当某个节点已经是一个词的结尾时，按下列方法修改其base值。

if ( base [i]==0)
    base [i]=-i
else
    base [i]=- base [i]

得到：

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	-1	1	1	0	1	-6	1	-8	-9	-1	-11	0	0	0	0	0	0	0	0
check	0	0	0	0	2	2	2	3	5	7	10	0	0	0	0	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷	阿拉伯	阿拉伯人

double array建好之后，如果词典中又动态地添加了一个新词，比如“阿拉根”，那么“阿拉”的所有子孙节点在double array中的位置要重新分配。

 

图2. 动态添加一个词

首先，把“阿拉伯”和“阿拉伯人”对应的base、check值清0，把“阿拉伯”和“阿拉伯人”从state数组中删除掉，把“阿拉”的base值清0。

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	-1	1	1	0	1	-6	0	-8	-9	0	0	0	0	0	0	0	0	0	0
check	0	0	0	0	2	2	2	3	5	0	0	0	0	0	0	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷

然后，按照上面step2所述的方法把“阿拉伯”、“阿拉根”插入到double array中。变量“根”、“伯”的编号是4和9，满足base[k+4]=base[k+9]=check[k+4]=check[k+9]=0的最小的k是6，所以base[7]=6，“阿拉伯”和“阿拉根”对应的下标是10和15。同理把“阿拉伯人”插入到double array中。

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	-1	1	1	0	1	-6	6	-8	-9	0	0	0	0	0	1	0	0	0	0
check	0	0	0	0	2	2	2	3	5	7	15	0	0	0	7	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷	阿拉根	阿拉伯人				阿拉伯

最后，遍历图2所示的DFA，当某个节点已经是一个词的结尾时按照step4中的方法修改其base值。

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	-1	1	1	0	1	-6	6	-8	-9	-10	-11	0	0	0	-1	0	0	0	0
check	0	0	0	0	2	2	2	3	5	7	15	0	0	0	7	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷	阿拉根	阿拉伯人				阿拉伯

 

double array建好之后，如何查询一个词是否在词典中呢？

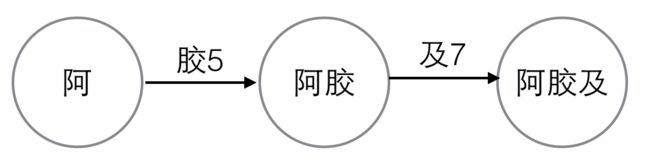
比如要查“阿胶及”，每个字的编号是已知的，我们画出状态转移图。

变量“阿”的编号是2，base[2]=1，变量“胶”的编号是5，base[2]+5=6，我们检查一下check[6]是否等于2。check[6]确实等于2，则继续看下一个状态转移。同时我们发现base[6]是负数，这说明“阿胶”已经是一个完整的词了。

继续看下一个状态转移，base[6]=-6，负数取其相反数，base[6]=6，变量“及”的编号是7，base[6]+7=13，我们检查一下check[13]是否等于6，发现不满足，则“阿胶及”不是一个词，甚至都是不是任意一个词的前缀。

github上一个日本人贡献了他的java版的Darts(Darts本来是一种Double Array Trie的C++实现)，代码如下：

import  java.io.BufferedInputStream;
import  java.io.BufferedOutputStream;
import  java.io.DataInputStream;
import  java.io.DataOutputStream;
import  java.io.File;
import  java.io.FileInputStream;
import  java.io.FileOutputStream;
import  java.io.IOException;
import  java.util.ArrayList;
import  java.util.Collections;
import  java.util.List;

/**
 * DoubleArrayTrie在构建双数组的过程中也借助于一棵传统的Trie树，但这棵Trie树并没有被保存下来，
 * 如果要查找以prefix为前缀的所有词不适合用DoubleArrayTrie，应该用传统的Trie树。
 *
 * @author zhangchaoyang
 *
 */
public  class  DoubleArrayTrie {
    private  final  static  int  BUF_SIZE =  16384 ; // 2^14，java采用unicode编码表示所有字符，每个字符固定用两个字节表示。考虑到每个字节的符号位都是0，所以又可以节省两个bit
    private  final  static  int  UNIT_SIZE =  8 ;  // size of int + int

    private  static  class  Node {
        int  code; // 字符的unicode编码
        int  depth; // 在Trie树中的深度
        int  left; //
        int  right; //
    };

    private  int  check[];
    private  int  base[];

    private  boolean  used[];
    private  int  size;
    private  int  allocSize; // base数组当前的长度
    private  List key; // 所有的词
    private  int  keySize;
    private  int  length[];
    private  int  value[];
    private  int  progress;
    private  int  nextCheckPos;
    int  error_;

    // 扩充base和check数组
    private  int  resize( int  newSize) {
        int [] base2 =  new  int [newSize];
        int [] check2 =  new  int [newSize];
        boolean  used2[] =  new  boolean [newSize];
        if  (allocSize >  0 ) {
            System.arraycopy(base,  0 , base2,  0 , allocSize); // 如果allocSize超过了base2的长度，会抛出异常
            System.arraycopy(check,  0 , check2,  0 , allocSize);
            System.arraycopy(used,  0 , used2,  0 , allocSize);
        }

        base = base2;
        check = check2;
        used = used2;

        return  allocSize = newSize;
    }

    private  int  fetch(Node parent, List siblings) {
        if  (error_ <  0 )
            return  0 ;

        int  prev =  0 ;

        for  ( int  i = parent.left; i < parent.right; i++) {
            if  ((length !=  null  ? length[i] : key.get(i).length()) < parent.depth)
                continue ;

            String tmp = key.get(i);

            int  cur =  0 ;
            if  ((length !=  null  ? length[i] : tmp.length()) != parent.depth)
                cur = ( int ) tmp.charAt(parent.depth) +  1 ;

            if  (prev > cur) {
                error_ = - 3 ;
                return  0 ;
            }

            if  (cur != prev || siblings.size() ==  0 ) {
                Node tmp_node =  new  Node();
                tmp_node.depth = parent.depth +  1 ;
                tmp_node.code = cur;
                tmp_node.left = i;
                if  (siblings.size() !=  0 )
                    siblings.get(siblings.size() -  1 ).right = i;

                siblings.add(tmp_node);
            }

            prev = cur;
        }

        if  (siblings.size() !=  0 )
            siblings.get(siblings.size() -  1 ).right = parent.right;

        return  siblings.size();
    }

    private  int  insert(List siblings) {
        if  (error_ <  0 )
            return  0 ;

        int  begin =  0 ;
        int  pos = ((siblings.get( 0 ).code +  1  > nextCheckPos) ? siblings.get( 0 ).code +  1
                : nextCheckPos) -  1 ;
        int  nonzero_num =  0 ;
        int  first =  0 ;

        if  (allocSize <= pos)
            resize(pos +  1 );

        outer:  while  ( true ) {
            pos++;

            if  (allocSize <= pos)
                resize(pos +  1 );

            if  (check[pos] !=  0 ) {
                nonzero_num++;
                continue ;
            }  else  if  (first ==  0 ) {
                nextCheckPos = pos;
                first =  1 ;
            }

            begin = pos - siblings.get( 0 ).code;
            if  (allocSize <= (begin + siblings.get(siblings.size() -  1 ).code)) {
                // progress can be zero
                double  l = ( 1.05  >  1.0  * keySize / (progress +  1 )) ?  1.05  :  1.0
                        * keySize / (progress +  1 );
                resize(( int ) (allocSize * l));
            }

            if  (used[begin])
                continue ;

            for  ( int  i =  1 ; i < siblings.size(); i++)
                if  (check[begin + siblings.get(i).code] !=