Implement Stack using Queues:使用队列表示栈

Implement the following operations of a stack using queues.

• push(x) -- Push element x onto stack.
• pop() -- Removes the element on top of the stack.
• top() -- Get the top element.
• empty() -- Return whether the stack is empty.

Example:

MyStack stack = new MyStack();

stack.push(1);
stack.push(2);  
stack.top();   // returns 2
stack.pop();   // returns 2
stack.empty(); // returns false

Notes:

• You must use only standard operations of a queue -- which means only push to back, peek/pop from front, size, and is empty operations are valid.
• Depending on your language, queue may not be supported natively. You may simulate a queue by using a list or deque (double-ended queue), as long as you use only standard operations of a queue.
• You may assume that all operations are valid (for example, no pop or top operations will be called on an empty stack).

思路：双队列实现的化用通俗的话讲就是来回折腾：

class MyStack {
    Queue q1;
    Queue q2;
    
    /** Initialize your data structure here. */
    public MyStack() {
        q1 = new LinkedList();
        q2 = new LinkedList();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        if(q1.isEmpty()){
            q1.offer(x);
            while(!q2.isEmpty()){
                q1.offer(q2.poll());
            }
        }else{
            q2.offer(x);
            while(!q1.isEmpty()){
                q2.offer(q1.poll());
            }
        }
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        if(!q1.isEmpty()){
            return q1.poll();
        }else if(!q2.isEmpty()){
            return q2.poll();
        }else{
            throw new RuntimeException();
        }
    }
    
    /** Get the top element. */
    public int top() {
        if(!q1.isEmpty()){
            return q1.peek();
        }else if(!q2.isEmpty()){
            return q2.peek();
        }else{
            throw new RuntimeException();
        }
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return q1.isEmpty()&&q2.isEmpty();
    }
}
/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

然鹅，更巧妙的方法是使用单栈，每次插入元素时将之前的所有元素都反转重新插入。

下面来源自：https://leetcode.com/problems/implement-stack-using-queues/solution/

(One Queue, push - $O(n)$, pop $O(1)$ )

The mentioned above two approaches have one weakness, they use two queues. This could be optimized as we use only one queue, instead of two.

Algorithm

Push

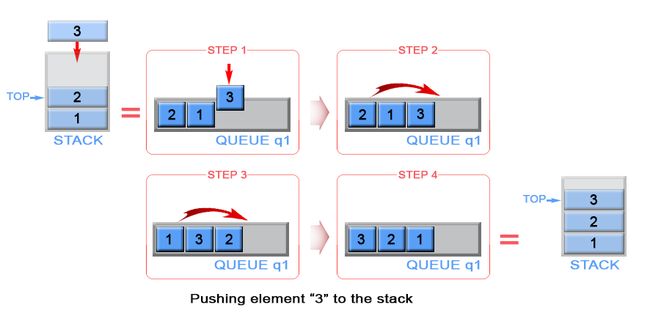
When we push an element into a queue, it will be stored at back of the queue due to queue's properties. But we need to implement a stack, where last inserted element should be in the front of the queue, not at the back. To achieve this we can invert the order of queue elements when pushing a new element.

Figure 5. Push an element in stack

Java

private LinkedList<Integer> q1 = new LinkedList<>();

// Push element x onto stack.
public void push(int x) {
    q1.add(x);
    int sz = q1.size();
    while (sz > 1) {
        q1.add(q1.remove());
        sz--;
    }
}

Complexity Analysis

• Time complexity : $O(n)$. The algorithm removes n elements and inserts $n+1$ elements to q1 , where n is the stack size. This gives $2n+1$ operations. The operations add and remove in linked lists has $O(1)$complexity.

• Space complexity : $O(1)$.

Pop

The last inserted element is always stored at the front of q1 and we can pop it for constant time.

Java

// Removes the element on top of the stack.
public void pop() {
    q1.remove();
}

Complexity Analysis

• Time complexity : $O(1)$.
• Space complexity : $O(1)$.

Empty

Queue q1 contains all stack elements, so the algorithm checks if q1 is empty.

// Return whether the stack is empty.
public boolean empty() {
    return q1.isEmpty();
}

Time complexity : $O(1)$.

Space complexity : $O(1)$.

Top

The top element is always positioned at the front of q1. Algorithm return it.

// Get the top element.
public int top() {
    return q1.peek();
}

Time complexity : $O(1)$.

Space complexity : $O(1)$.

Analysis written by: @elmirap.