深度学习方法：受限玻尔兹曼机RBM（二）网络模型

欢迎转载，转载请注明：本文出自Bin的专栏blog.csdn.net/xbinworld。
技术交流QQ群：433250724，欢迎对算法、技术、应用感兴趣的同学加入

上解上一篇RBM（一）基本概念，本篇记叙一下RBM的模型结构，以及RBM的目标函数（能量函数），通过这篇就可以了解RBM到底是要求解什么问题。在下一篇（三）中将具体描述RBM的训练/求解方法，包括Gibbs sampling和对比散度DC方法。

RBM模型结构

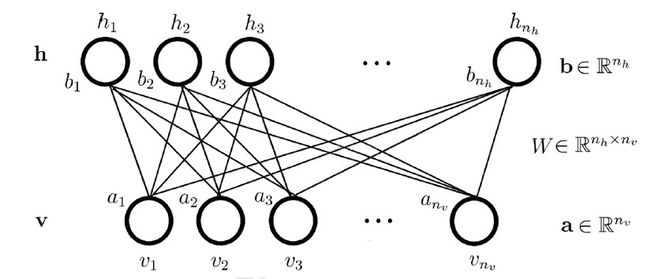
因为RBM隐层和可见层是全连接的，为了描述清楚与容易理解，把每一层的神经元展平即可，见下图[7]，本文后面所有的推导都采用下图中的标记来表示。

再重提一下，经典的RBM模型中的神经元都是binary的，也就是说上面图中的神经元取值都是{ 0,1}的。实际上RBM也可以做实数性的model，不过这一块可以先放一放，先来看binary的基本model。

RBM能量函数

RBM是一个能量模型（Energy based model, EBM），是从物理学能量模型中演变而来；能量模型需要做的事情就是先定义一个合适的能量函数，然后基于这个能量函数得到变量的概率分布，最后基于概率分布去求解一个目标函数（如最大似然）。RBM的过程如下：

我们现在有的变量是(v,h)，包括隐层和可见层神经元；参数包括θ=(W,a,b)。能量函数定义：

Eθ(v,h)=−∑i=1nvaivi−∑j=1nhbjhj−∑i=1nv∑j=1nhhjwj,ivi

如果写成向量/矩阵的形式，则为：

Eθ(v,h)=−aTv−bTh−hTWv

那么，可以得到变量(v,h)的联合概率分布是：

Pθ(v,h)=1Zθe−Eθ(v,h)

其中， Zθ称为归一化因子，作用是使得概率之和（或者积分）为1，形式为：

Zθ=∑v,he−Eθ(v,h)

在上面所有算式中，下标 θ都表示在参数 θ=(W,a,b)下的表达，为了书写的简洁性，本文余下部分如果没有特殊指定说明，就省略下标 θ了，但含义不变。

OK，当我们有了联合概率分布，如果想求观察数据（可见层）的概率分布P(v)，则求边缘分布：

P(v)=∑hP(v,h)=1Z∑he−E(v,h)

相对应的，如果想求隐层单元的概率分布P(h)，则求边缘分布：

P(h)=∑vP(v,h)=1Z∑ve−E(v,h)

当然，我们不太可能直接计算Z，因为Z的求和中存在指数项种可能——2nv+nh种取值。接下来考虑条件概率，即可见层神经元状态给定时，（任意）隐藏层神经元状态为1的概率，即P(hk=1|v)。类似的也可以求P(vk=1|h)，方法也是差不多的，下面就只对P(hk=1|v)进行描述。我们可以推导出：

P(hk=1|v)==sigmoid(bk+∑j=1nvwkjvj)

以及

P(vk=1|h)==sigmoid(ak+∑j=1nhwjkhj)

可以直接知道结果即可，证明可以跳过。这里我们可以看到，sigmoid是一种激励函数，因此才把RBM也叫做一种神经网络模型。

---

证：以下记h−k表示隐藏层神经元k以外的神经元。

P(hk=1|v)=P(hk=1|h−k,v)=P(hk=1,h−k,v)P(h−k,v))=P(hk=1,h−k,v)P(hk=1,h−k,v))+P(hk=0,h−k,v))=1Ze−E(hk=1,h−k,v)1Ze−E(hk=1,h−k,v))+1Ze−E(hk=0,h−k,v))=11+e−E(hk=0,h−k,v))+E(hk=1,h−k,v)=11+e−(bk+∑nvj=1wkjvj)=sigmoid(bk+∑j=1nvwkjvj)

---

因为假设同层神经元之间相互独立，所以有：

P(h|v)=∏j=1nhP(hj|v)P(v|h)=∏i=1nvP(vi|h)

RBM目标函数

假设给定的训练集合是S={ vi}，总数是ns，其中每个样本表示为vi=(vi1,vi2,…,vinv)，且都是独立同分布i.i.d的。RBM采用最大似然估计，即最大化

lnLS=ln∏i=1nsP(vi)=∑i=1nslnP(vi)

RBM的求解问题就是如何最大化似然估计，在下一篇中我会描述常用的求解方法：Gibbs Sampling以及对比散度方法，算是RBM的核心吧。本篇就到这里。

---

觉得有一点点价值，就支持一下哈！花了很多时间手打公式的说~更多内容请关注Bin的专栏

---

参考资料
[1] http://www.chawenti.com/articles/17243.html
[2] 张春霞，受限波尔兹曼机简介
[3] http://www.cnblogs.com/tornadomeet/archive/2013/03/27/2984725.html
[4] http://deeplearning.net/tutorial/rbm.html
[5] Asja Fischer, and Christian Igel，An Introduction to RBM
[6] G.Hinton, A Practical Guide to Training Restricted Boltzmann Machines
[7] http://blog.csdn.net/itplus/article/details/19168937
[8] G.Hinton, Training products of experts by minimizing contrastive divergence, 2002.
[9] Bengio, Learning Deep Architectures for AI, 2009

转载于:https://www.cnblogs.com/yihaha/p/7265323.html