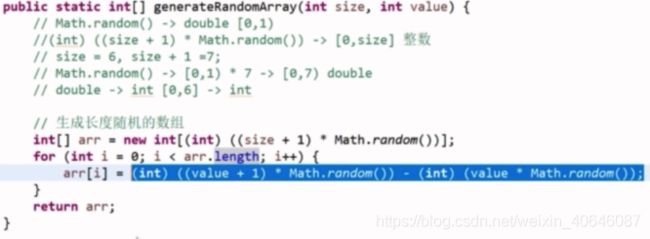
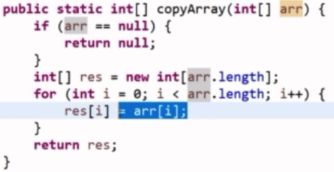
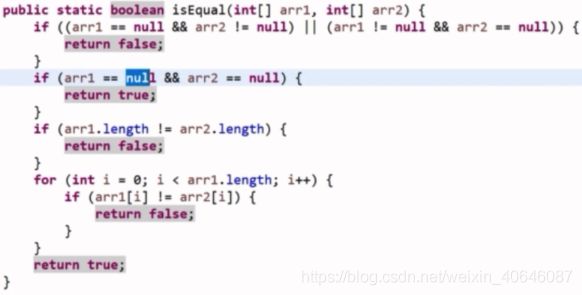
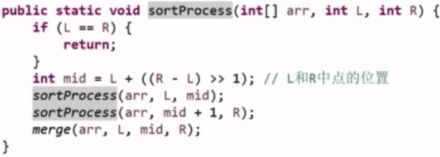
javascript牛客网剑指offer

输入一个链表，输出该链表中倒数第k个结点。

思路：用两个指针，让他们相差K，首先让a先走k步，这样确保a、b相差K，之后同时走，限制条件是a走到链尾，此时的b就是倒数第k个节点

function FindKthToTail(head, k)
    {
        // write code here
        if(head == null || k == 0)
        {
            return null;
        }

        var a = head;
        var b = null;
        for (var i = 0; i < k - 1; i++)
        {
            if(a.next != null)
            {
                a = a.next;
            }
            else
            {
                return null;
            }
        }

        b = head;
        while (a.next != null)
        {
            a = a.next;
            b = b.next;
        }
        return b;
    }

输入一个链表，反转链表后，输出新链表的表头。

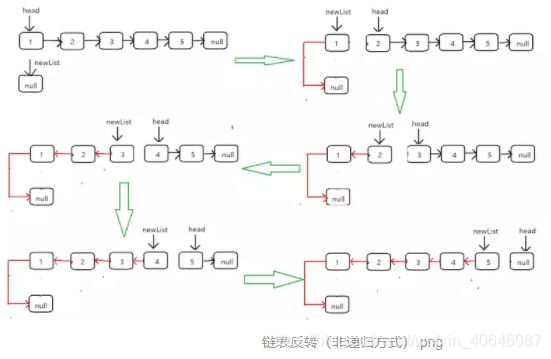
思路：根据下图，先给定一个空的链表newList，然后判断传入的链表head是不是空链表或者链表元素只有一个，如果是，直接返回就可以。如果不是，则对链表进行迭代，然后给一个临时变量temp存储head.next,然后改变head.next的指向newList,然后把head赋值给newList,接着让head等于临时变量temp，就这样一直迭代完整个链表，返回newList就可以

function ReverseList(pHead)
{
    // write code here
    var newlist=null;
    var temp=null;
    while(pHead!=null){
        temp=pHead.next; //用temp保存原链表头指针的下一位，防止改变指针后，找不到
        pHead.next=newlist;//第一次循环，反转链表后，头指针为空，将newlist赋值给pHead.next
        newlist=pHead;//newlist记录新链表，每轮循环进行更新
        pHead=temp;//将原链表的头部向后移一位，继续上述过程，当原链表的头部为空，跳出循环
    }
    return newlist;
}

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

function Merge(pHead1, pHead2)
{
    // write code here 递归
    if(pHead1 == null)return pHead2;
    if(pHead2 == null)return pHead1;//一个链表为空，直接返回另一个
    var result = null;
    if(pHead1.val < pHead2.val){
        result = pHead1;
        result.next = Merge(pHead1.next, pHead2); //递归调用链表1的下一位
    }else{
        result = pHead2;
        result.next = Merge(pHead1, pHead2.next);//递归调用链表2的下一位
    }
    return result;
}

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

function HasSubtree(pRoot1, pRoot2)
{
    // write code here二叉树问题，经常和递归有关
    var res=false;
    if(pRoot1 == null || pRoot2 == null){
        return false;
    }
    if(pRoot1.val == pRoot2.val) res = jixu(pRoot1, pRoot2); //两个树的根节点是否相同
    if(!res) res = HasSubtree(pRoot1.left, pRoot2);//A的左子树和B树的根节点是否相同
    if(!res) res = HasSubtree(pRoot1.right, pRoot2);//A的右子树和B树的根节点是否相同
    return res;
}
function jixu(pRoot1, pRoot2){
    //注意这里先判断pRoot2，要求是判断B是不是A的子结构，若先判断pRoot1,会有错误情况弹出
    if(pRoot2 == null) return true;
    if(pRoot1 == null) return false;
    if(pRoot1.val != pRoot2.val) return false;
    return jixu(pRoot1.left, pRoot2.left)&& jixu(pRoot1.right, pRoot2.right);
}

操作给定的二叉树，将其变换为源二叉树的镜像。

function Mirror(root)
{
    // write code here
    if(root == null) return;
    [root.left,root.right]=[root.right,root.left];
    Mirror(root.left);
    Mirror(root.right);
    return root;
}

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

function printMatrix(matrix)
{
    // write code here
    if(matrix == null){
        return null;
    }
    var hang = matrix.length,lie = matrix[0].length;
    var start = 0,res=[];
    //循环条件很重要
    while(hang > start*2 && lie > start*2){
        res = res.concat(bianli(matrix,hang,lie,start));
        start++;
    }
    return res;
} 
function bianli(matrix,hang,lie,start){
    var endX = lie-1-start,endY = hang-1-start,res=[];
    //打印上行
    for(var i=start;i<=endX;i++){
        res.push(matrix[start][i]);
    }
    //打印右列
    for(var i=start+1;i<=endY;i++){
        res.push(matrix[i][endX]);
    }
    //打印下行
    for(var i=endX-1;i>=start&&endY>start;i--){
        res.push(matrix[endY][i]);
    }
    //打印左列
    for(var i=endY-1;i>=start+1&&endX>start;i--){
        res.push(matrix[i][start]);
    }
    return res;
}

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

思路：借用一个辅助的栈，遍历压栈顺序，先讲第一个放入栈中，这里是1，然后判断栈顶元素是不是出栈顺序的第一个元素，这里是4，很显然1≠4，所以我们继续压栈，直到相等以后开始出栈，出栈一个元素，则将出栈顺序向后移动一位，直到不相等，这样循环等压栈顺序遍历完成，如果辅助栈还不为空，说明弹出序列不是该栈的弹出顺序。

举例：

入栈1,2,3,4,5

出栈4,5,3,2,1

首先1入辅助栈，此时栈顶1≠4，继续入栈2

此时栈顶2≠4，继续入栈3

此时栈顶3≠4，继续入栈4

此时栈顶4＝4，出栈4，弹出序列向后一位，此时为5，,辅助栈里面是1,2,3

此时栈顶3≠5，继续入栈5

此时栈顶5=5，出栈5,弹出序列向后一位，此时为3，,辅助栈里面是1,2,3

….

依次执行，最后辅助栈为空。如果不为空说明弹出序列不是该栈的弹出顺序。

function IsPopOrder(pushV, popV)
{
    // write code here
        if(pushV == null || pushV == null || pushV.length == 0 || pushV.length == 0
           || pushV.length != popV.length) return false;
        var st = [];  //创建一个栈，可以使用栈的方法
        var i = 0;
        var j = 0;
        st.push(pushV[i++]);
        while(j <= popV.length-1){
            while(popV[j] != st[st.length-1]){
                if(i == pushV.length) return false;
                st.push(pushV[i++]);
            }
            j++;
            st.pop();
        }
        return true;
}

从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。

思路：按层输出，遵循先进先出的原则，使用一个队列，两个数组，两个变量

function Print(pRoot) {
  const queue = [],
    res = [];
  if (pRoot === null) {
    return res;
  }
  queue.push(pRoot);
  let nextLevel = 0; // 下一层节点个数
  let toBePrinted = 1; // 这一层还有多少个节点要打印
  let list = []; // 存放每一层节点
  while (queue.length) {
    const pNode = queue.shift();  
    list.push(pNode.val);   // 移除队列，加入list数组中
    if (pNode.left !== null) {
      queue.push(pNode.left);
      nextLevel++;
    }
    if (pNode.right !== null) {
      queue.push(pNode.right);
      nextLevel++;
    }
    toBePrinted--;      //nextLevel与 toBePrinted相关，当toBePrinted === 0时，表示上层全部节点打印完成
    if (toBePrinted === 0) {
      res.push(list);
      list = [];
      toBePrinted = nextLevel;
      nextLevel = 0;
    }
  }
  return res;
}

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

function PrintFromTopToBottom(root)
{
    // write code here广度优先遍历 队列的规则 先进先出 push在队尾加入，shift是在队首删除
    var queue=[];
    var dian=[];
    if(root!=null){
        queue.push(root);
        while(queue.length!=0){
            var node=queue.shift();
            dian.push(node.val);
            if(node.left!=null){
                queue.push(node.left);
            }
            if(node.right!=null){
                queue.push(node.right);
            }
        }
    }
    return dian;
}

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

思路：首先了解二叉搜索树的概念，之后是后序遍历，最后一位是根节点，那么遍历数组，出现第一位大于根节点的点，则为右子树的第一个节点(判断点是否满足条件)，在该节点之前的点则为左子树，分为左右两部分，之后进行递归操作。

 function VerifySquenceOfBST(sequence)
    {
        // write code here
        if(!sequence.length) return false;
        return judge(sequence,0,sequence.length-1);
    }
    function judge(a,start,end){
        if(start >= end) return true;
        for (var i = start; i < end; i++) {
            if(a[i] > a[end]) break;
        }
        for(var j=i;j

输入一颗二叉树的跟节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)

思路分析：首先思考节点值的和为输入的整数，每条路径都一定是从根节点到叶子节点，在数据结构中从根节点到叶子节点的遍历称之为深度优先遍历DFS。因此整个过程可以采用先序遍历方式的DFS，即根节点》左子树》右子树。随后考虑一次遍历完成后的处理，当一次遍历完成后，如果输入整数值恰好等于节点值之和，则输出这条路径并且回退一个节点；如果不等于则直接回退一个节点，即回退到当前节点的父节点，如果该父节点有右孩子，则继续遍历，否则继续回退。考虑回退到根节点，此时如果它有右孩子，则继续遍历，否则整个DFS结束。
用图片理解过程，里面的remove对应自己程序中的list.pop函数

黑色图片是array.of的作用，这里是ES6语法对的应用

 function FindPath(root, expectNumber)
 {
        // write code here 先序遍历的深度遍历，根-左-右  使用栈，先进后出，插入push 出、删pop
        var list = [],listall = [];
        return path(root, expectNumber, list, listall);
    
 }
function path(root, expectNumber, list, listall){
    if(!root)return listall;
    list.push(root.val);
    var x = expectNumber - root.val;
    if(root.left == null && root.right == null && x == 0){
        listall.push(Array.of(...list));      //Array.of方法用于将一组值，转换为数组。Array.of总是返回参数值组成的数组。
                                             //如果没有参数，就返回一个空数组。
    }
    path(root.left,x, list, listall);
    path(root.right,x, list, listall);
    list.pop();//退回到父节点
    return listall;
}

输入一棵二叉树，判断该二叉树是否是平衡二叉树。

function IsBalanced_Solution(pRoot)
{
    // write code here 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
  if (pRoot == null) return true;
  let leftLen = TreeDepth(pRoot.left);
  let rightLen = TreeDepth(pRoot.right);
  return Math.abs(rightLen - leftLen) <= 1 && IsBalanced_Solution(pRoot.left)
         && IsBalanced_Solution(pRoot.right);
}

function TreeDepth(pRoot) {
  if (pRoot == null) return 0;
  let leftLen = TreeDepth(pRoot.left);
  let rightLen = TreeDepth(pRoot.right);
  return Math.max(leftLen, rightLen) + 1;
}

二叉树的深度

var maxDepth = function(root) {
    if (root === null) { //注意等号
        return 0;
    } else {
        var leftDepth = maxDepth(root.left),
            rightDepth = maxDepth(root.right);

        var childDepth = leftDepth > rightDepth ? leftDepth : rightDepth;

        return childDepth + 1;//根节点不为空高度至少为1
    }
};

字符串去重或者字符串去重

var c='aaaaaaaaaaaaaaabbbbbbbbbbbbbbbbbccccccccccccc';
function f(a) {
    var b='';
    for (var i=0;i

统计数组中 某个 元素出现的次数

function times(arr){
    var m=0,times=0;   //m是数组中的元素，times用来统计出现的次数
    // for循环遍历arr数组
    for(var i=0;i

统计数组中 每个 元素出现的次数

const arr = [1,1,1,2,3,4,4,4,2,3,7,4];
function gets(arr){
    var obj = {};
    for(var i = 0;i

统计数组中的重复元素，将其从小到大排序

function unique1(arr){
    var hash=[];
    var a=[];
    for (var i = 0; i < arr.length; i++) {
        if(hash.indexOf(arr[i])==-1){
            hash.push(arr[i]);     //这一步可以打印出去重的数组
        }else {
            a.push(arr[i]);
        }
    }
    var b=[];
    for (var i = 0; i < a.length; i++) {
        if (b.indexOf(a[i]) == -1) {
            b.push(a[i]);
        }
    }
    return sort(b);    
}

function sort(m){
    var temp=0;
    for(var i=0;im[j+1]){
                temp=m[j];
                m[j]=m[j+1];
                m[j+1]=temp;
            }
        }
    }
    return m;
}

var arr=[2,8,5,0,5,2,6,7,2];
console.log(unique1(arr));

判断一棵树是否是二叉搜索树

var list=[];
function isTree( root){
    //中序遍历
    if(root == NULL)  return;
    isTree(root.left);
    list.push(root.val);
    isTree(root.right);
}
function  isBST (root){
    //给定了树的根节点root
    isTree(root);
    for(int i = 1; i < list.length; i++)
        if(list[i-1] >= list[i])
          return false;
          return true;
}

对数器

一个正确的数组

拷贝数组