机器学习笔记——朴素贝叶斯

贝叶斯定理

概率事件

事件A发生的概率记为$P(A)$，事件B发生的概率记为$P(B)$，

条件概率

在事件A发生后发生B事件的概率记为$P(B|A)$，在事件B发生后发生事件A的概率为$P(A|B)$，

联合概率

事件A和B同时发生的概率为联合概率，记为为P(A，B)（即P(A和B)）那么$$P(A,B)=P(A)P(B|A)=P(B)P(A|B)$$
那么我们很容易得到
$$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$
这就是贝叶斯公式，朴素贝叶斯算法也是基于此公式

朴素贝叶斯算法

极大似然估计

输入：有训练数据及$T=\{(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)\}$， 其中$x_i=(x_i^{(1)},x_i^{(2)},\dots ,x_i^{(n)}{)}^T$，$x_i^{(j)}$是第$i$个样本的第$j$个特征，$x_i^{(j)}\in \{a_{j1},a_{j2},\dots ,a_{j{S}_j}\}$，$a_{jl}$是第$j$个特征可能取得第$l$个值，$y$的类标记集合为$\{(c_1),(c_2),\dots ,(c_K)\}$；
实例：$x$；
输出：实例$x$的分类。
1）计算先验概率及条件概率
$$P(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)}{N},k=1,2,\dots ,K$$
$$P(X^{(j)}=a_{jl}|Y=c_k)=\frac{{\sum }_{i=1}^{N}I(x_i^{(j)}=a_{jl},y_i=c_k)}{{\sum }_{i=1}^{N}I(y_i=c_k)}$$
其中$j=1,2,\dots ,n;l=1,2,\dots ,S_j;k=1,2,\dots ,K$
2）对于给定的实例$x=(x^{(1)},x^{(2)},\dots ,x^{(n)}{)}^T$，计算
$$P(Y=c_k)=\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k),k=1,2,\dots ,K$$
3）确定实例x的类
$$y=argma{x}_{c_k}P(Y=c_k)\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)$$

贝叶斯估计

用极大似然估计可能会出现估计概率值为0的情况，解决方法是采用贝叶斯估计。条件概率的贝叶斯估计是

$$P_{\lambda }(X^{(j)}=a_{jl}|Y=c_k)=\frac{{\sum }_{i=1}^{N}I(x_i^{(j)}=a_{jl},y_i=c_k)+\lambda }{{\sum }_{i=1}^{N}I(y_i=c_k)+S_j\lambda }$$
其中$\lambda >=0$，通常$\lambda =1$，这是成为拉普拉斯平滑，对于任何$l=1,2,\dots ,S_j,k=1,2,\dots ,K$，有
$$P_{\lambda }(X^{(j)}=a_{jl}|Y=c_k)>0$$
$$\sum _{l=1}^{S_j}{P}_{\lambda }(X^{(j)}=a_{jl}|Y=c_k)=1$$
先验概率的贝叶斯估计是
$$P_{\lambda }(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)+\lambda }{N+K\lambda }$$

代码实现

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB

# 构造训练数据集
x_cls1 = np.concatenate((np.random.randn(300).reshape(-1, 1), np.random.randn(300).reshape(-1, 1)), axis=1)
y_cls1 = np.zeros((300))
x_cls2 = np.concatenate(((np.random.randn(300)+4).reshape(-1, 1), np.random.randn(300).reshape(-1, 1)), axis=1)
y_cls2 = np.ones((300))

x = np.round(np.concatenate((x_cls1, x_cls2), axis=0), 1)
y = np.concatenate((y_cls1, y_cls2), axis=0)

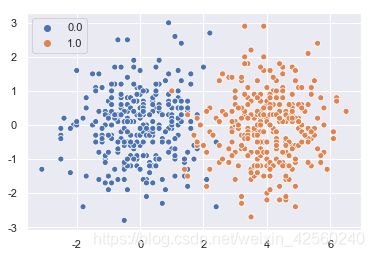
用散点图查看数据

sns.scatterplot(x[:, 0], x[:, 1], hue=y)

# 把训练集分割成训练集和测试集
x_train, x_test, y_train, y_test = \
    train_test_split(x, y, test_size=0.3)
# 训练模型
clf = GaussianNB()
clf.fit(x_train, y_train)

print("test score: %.2f" % clf.score(x_test, y_test))

test score: 0.98
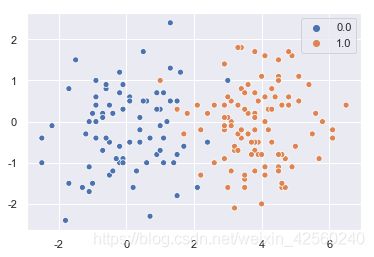
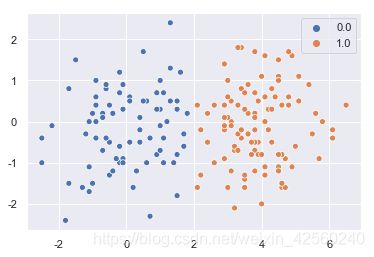
测试集散点图和预测散点图分别为

参考文献

李航 《统计学习方法 第二版》