间接平差编程初探
题目:
武汉大学出版社的《误差理论与测量平差基础》(第三版)第7章,例7-3,根据题目的已知条件,计算未知点D的坐标、验后单位权中误差、点位中误差、观测值的平差值及其方差协方差阵。
详细设计
编程设计
编程结构体
struct QSxy
{
public string name;
public string types;
public double x;
public double y;
}
public struct QSl
{
public string name;
public string types;
public double dd;
public double mm;
public double ss;
}
struct QSs
{
public string name;
public string types;
public double s;
}
public struct GC
{
public string cezhan;
public string zhaozhun;
public string types;
public double dd;
public double mm;
public double ss;
}
struct dfm //度分秒
{
public double dd;
public double mm;
public double ss;
}
为了将所有数据的结构体保存起来,故需要定义列表储存:
List<QSl> QSl_list;
List<QSs> QSs_list;
List<QSxy> QSxy_list;
List<GC> GC_list;
public Form1()
{
QSl_list = new List<QSl>();
QSs_list = new List<QSs>();
QSxy_list = new List<QSxy>();
GC_list = new List<GC>();
InitializeComponent();
}
文件打开
private void 打开OToolStripButton_Click(object sender, EventArgs e)
{
OpenFileDialog pdlg = new OpenFileDialog();
pdlg.Filter = "文本文件|*.txt|所有文件|*.*";
DialogResult rt = pdlg.ShowDialog();
if (rt == DialogResult.OK)
{
string filename = pdlg.FileName;
richTextBox1.LoadFile(filename, RichTextBoxStreamType.PlainText);
}
}
字符串分割
int iRows = richTextBox1.Lines.Length;
int ii = 1;
for (ii = 1; ii < iRows; ii++)
{
string stl = richTextBox1.Lines[ii];
if (stl.Trim() == "")
{
continue;
}
string[] starray = stl.Split(',');
if (starray.Length == 1)
{
break; }
}
string tem = "";
for (int i = 1; i < iRows; i++)
{
string stl = richTextBox1.Lines[i];
if (stl.Trim() == "")
{
continue;
}
string[] starray = stl.Split(',');
int Cols = starray.Length;
if (i < ii)
{
switch (Cols)
{
case 4:
{
QSxy qSxy = new QSxy();
qSxy.name = starray[0];
qSxy.types = "xy";
qSxy.x = double.Parse(starray[2]);
qSxy.y = double.Parse(starray[3]);
QSxy_list.Add(qSxy);
break;
}
case 3:
{
QSs ss = new QSs();
ss.name = starray[0];
ss.types = "S";
ss.s = double.Parse(starray[2]);
QSs_list.Add(ss);
break;
}
case 5:
{
QSl sl = new QSl();
sl.name = starray[0];
sl.types = "L";
sl.dd = double.Parse(starray[2]);
sl.mm = double.Parse(starray[3]);
sl.ss = double.Parse(starray[4]);
QSl_list.Add(sl);
break;
}
}
}
else
{
switch (Cols)
{
case 1:
{
tem = starray[0];
break;
}
case 5:
{
GC gC = new GC();
gC.cezhan = tem;
gC.zhaozhun = starray[0];
gC.types = "L";
gC.dd = double.Parse(starray[2]);
gC.mm = double.Parse(starray[3]);
gC.ss = double.Parse(starray[4]);
GC_list.Add(gC);
break;
}
}
}
}
///显示-
richTextBox1.Text = "-------------------------------起算数据显示-----------------------------\r\n";
foreach(QSl sl in QSl_list)
{
string sData = String.Format("{0,12:F0} {1,12:F0} {2,12:F2} {3,12:F2} {4,12:F2}\r\n", sl.name,sl.types,sl.dd,sl.mm,sl.ss);
richTextBox1.Text += sData;
}
richTextBox1.Text += "------------------------------观测数据显示------------------------------\r\n";
foreach (GC gs in GC_list)
{
string sgs = String.Format("{0,4:F0} {1,4:F0} {2,12:F0} {3,12:F2} {4,12:F2} {5,12:F2}\r\n", gs.cezhan, gs.zhaozhun,gs.types,gs.dd, gs.mm, gs.ss);
richTextBox1.Text += sgs;
}
平差计算
double[] a = new double[10];
for(int i =0;i<10;i++)
{
a[i] = Jiaodu.AngtoRad(GC_list[i]);
}
double xd0=(QSxy_list[1].x*1/(Math.Tan(a[9]-a[8]))+ QSxy_list[0].x * 1 / (Math.Tan(a[6] - a[5]))- QSxy_list[0].y+ QSxy_list[1].y)/((1/Math.Tan(a[6] - a[5]))+ (1 / Math.Tan(a[9] - a[8])));
double yd0= (QSxy_list[1].y * 1 / (Math.Tan(a[9] - a[8])) + QSxy_list[0].y * 1 / (Math.Tan(a[6] - a[5])) + QSxy_list[0].x - QSxy_list[1].x) / ((1 / Math.Tan(a[6] - a[5])) + (1 / Math.Tan(a[9] - a[8])));
double[] ZJ = new double[5];
//写出已知点坐标
double xb = QSxy_list[0].x;
double yb = QSxy_list[0].y;
double xa = QSxy_list[1].x;
double ya = QSxy_list[1].y;
double xc = QSxy_list[2].x;
double yc = QSxy_list[2].y;
//求方位角
double afab = Math.Atan((yb - ya) / (xb - xa));//已知
double afac= Math.Atan((yc - ya) / (xc - xa));//已知
double afad = Math.Atan((yd0 - ya) / (xd0 - xa));
double afcd = Math.Atan((yd0 - yc) / (xd0 - xc));
double afbd = Math.Atan((yd0 - yb) / (xd0 - xb));
//求各测站零方位角
ZJ[0] = ((afab - Jiaodu.AngtoRad(GC_list[5])) + (afac - Jiaodu.AngtoRad(GC_list[7])) + (afad - Jiaodu.AngtoRad(GC_list[6]))) / 3;//a
ZJ[1] = ((-afab - Jiaodu.AngtoRad(GC_list[9])) + (afbd - Jiaodu.AngtoRad(GC_list[8])))/2;//b
ZJ[2] = (-afac - Jiaodu.AngtoRad(GC_list[3]) + (afcd - Jiaodu.AngtoRad(GC_list[4]))) / 2;//c
ZJ[3] = (-afcd - Jiaodu.AngtoRad(GC_list[0]) - afad - Jiaodu.AngtoRad(GC_list[1]) - afbd - Jiaodu.AngtoRad(GC_list[2])) / 3;
//计算改正数方程系数
const double rou = 206265;
double[] A = new double[3];
double[] B = new double[3];
A[0] = rou * (yd0 - ya) / (Math.Sqrt(Math.Pow(yd0 - ya, 2) + Math.Pow(xd0 - xa, 2)))/10;//da
A[1] = rou * (yd0 - yb) / (Math.Sqrt(Math.Pow(yd0 - yb, 2) + Math.Pow(xd0 - xb, 2))) / 10;//bd
A[2] = rou * (yd0 - yc) / (Math.Sqrt(Math.Pow(yd0 - yc, 2) + Math.Pow(xd0 - xc, 2))) / 10;//cd
B[0] = rou * (xd0 - xa) / (Math.Sqrt(Math.Pow(yd0 - ya, 2) + Math.Pow(xd0 - xa, 2))) / 10;//ad
B[1] = rou * (xd0 - xb) / (Math.Sqrt(Math.Pow(yd0 - yb, 2) + Math.Pow(xd0 - xb, 2))) / 10;//bd
B[2] = rou * (xd0 - xc) / (Math.Sqrt(Math.Pow(yd0 - yc, 2) + Math.Pow(xd0 - xc, 2))) / 10;//cd
//此时bxd,byd的单位是dm
double[] _l=new double[10];
_l[0] = afab - ZJ[0] - Jiaodu.AngtoRad(GC_list[5]);
_l[1] = afad - ZJ[0] - Jiaodu.AngtoRad(GC_list[6]);
_l[2] = afac - ZJ[0] - Jiaodu.AngtoRad(GC_list[7]);
_l[3] = -afab - ZJ[1] - Jiaodu.AngtoRad(GC_list[9]);
_l[4] =afbd - ZJ[1] - Jiaodu.AngtoRad(GC_list[8]);
_l[5] = -afac - ZJ[2] - Jiaodu.AngtoRad(GC_list[3]);
_l[6] = afcd - ZJ[2] - Jiaodu.AngtoRad(GC_list[4]);
_l[7] = -afcd - ZJ[0] - Jiaodu.AngtoRad(GC_list[0]);
_l[8] = -afad - ZJ[0] - Jiaodu.AngtoRad(GC_list[1]);
_l[9] = -afbd - ZJ[0] - Jiaodu.AngtoRad(GC_list[2]);
//计算 dc da db
double[] ones = new double[10];
for (int i=0;i<10;i++)//zd的系数矩阵
{
ones[i] = -1;
}
double[] xd = new double[10] {
-A[2],A[0],A[1],0,A[2],0,-A[0],0,A[1],0};
double[] yd = new double[10] {
-B[2], B[0], B[1], 0, B[2], 0, -B[0], 0, B[1], 0 };
double[,] Bx = new double[3,10];
for (int i=0;i<10;i++)
{
Bx[0,i] = ones[i]; }
for (int i = 0; i < 10; i++)
{
Bx[1,i] = xd[i]; }
for (int i = 0; i < 10; i++)
{
Bx[2,i] = yd[i]; }
Matrix BX = new Matrix(3, 10);
for (int i=0;i<3;i++)
{
for(int j=0;j<10;j++)
{
BX[i,j] = Bx[i,j]; }
}
Matrix BXT = new Matrix(10,3);
BXT = BX.Transpose();
Matrix L = new Matrix(1, 10);
Matrix LT = new Matrix(10, 1);
for (int i=0;i<10;i++)
{
L[1, i] = _l[i]; }
LT = L.Transpose();
Matrix BTPBni = new Matrix(3,3);
BTPBni = BX* BXT;
BTPBni = BTPBni.InvertGaussJordan();
Matrix BTPL = new Matrix(3, 1);
BTPL = BX * L;
Matrix pingchazhi = new Matrix(3, 1);
pingchazhi = BTPBni * BTPL;//平差值
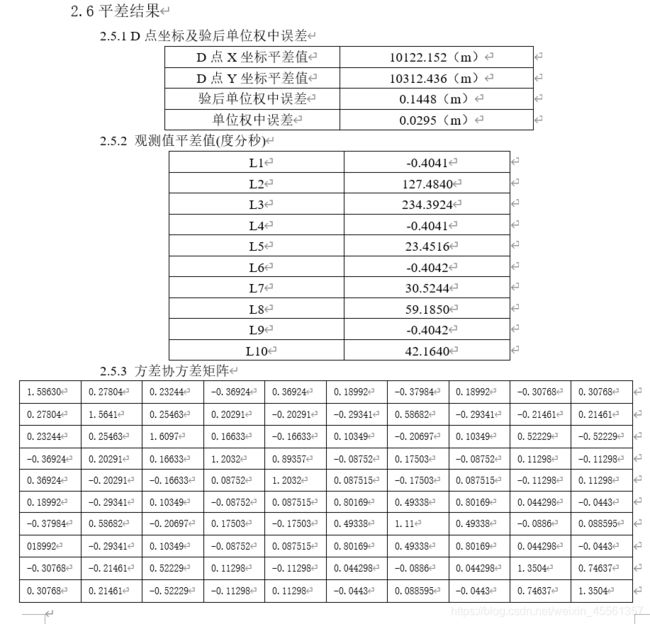
double XDba = xd0 + pingchazhi[2, 1];
double YDba = yd0 + pingchazhi[3, 1];//D点坐标
Matrix sgm0=new Matrix();
sgm0 = (pingchazhi.Transpose() * pingchazhi).Multiply(1 / 4); //验后单位权中误差
Matrix sgmd0 = new Matrix();
sgmd0 = sgm0 * Math.Sqrt(Math.Pow(XDba,2)+Math.Pow(YDba,2));
richTextBox1.Clear();
string s =string.Format("D点坐标是:\nx:{0} y:{1}\r\n",XDba,YDba);
richTextBox1.Text = s;
string ssgm0 = string.Format("验后单位权中误差:{0}",sgm0);
string sxfc = string.Format("方差阵:{0}",xfc);
richTextBox1.Text += ssgm0;
richTextBox1.Text += sxfc;