综合评价与决策方法(一)——TOPSIS法的原理
综合评价与决策方法
- 综述
- 理想解法
-
- 方法和原理
- TOPSIS法的算法步骤
- 例题
-
-
- 参考文献
-
综述
评价方法一般分为两类。一类是主观赋权法,多数采取综合咨询评分确定权重,如:综合指数法、模糊综合评价法、层次分析法、功效系数法等。另一类是客观赋权法,根据各指标之间的相关关系或各指标值变异程度来确定权数,如:主成分分析法、因子分析法、理想解法等。
目前,主要使用的评价方法有:主成分分析法、因子分析法、TOPSIS法、秩和比法、灰色关联法、熵权法、层次分析法、模糊评价法、物元分析法、聚类分析法、价值工程法、神经网络法等。
理想解法
当前已有许多解决多属性决策的排序法:理想点法、简单线性加权法、加权平方和法、主成分分析法、功效系数法、可能满意法、交叉增援矩阵法等。
接下来介绍的是理想解法,该方法通过构造评价问题的正理想解和负理想解(各指标的最优解和最劣解),通过计算每个方案到理想方案的相对贴近度,即靠近正理想解和负理想解的程度,来对方案进行排序,从而选出最优方案。
方法和原理
设多属性决策方案集为 D = d 1 , d 2 , . . . d m D={d_1,d_2,...d_m} D=d1,d2,...dm,衡量方案优劣的属性变量为 x 1 , . . . , x n x_1,...,x_n x1,...,xn,这时方案集 D D D中的每个方案 d i ( i = 1 , . . . , m ) d_i(i=1,...,m) di(i=1,...,m)为n个属性值构成的向量是 [ a i 1 , . . . , a i n ] [a_i1,...,a_in] [ai1,...,ain],它作为 n n n维空间中的一个点,能唯一地表征方案 d i d_i di。
正理想解 C ∗ C^* C∗是一个方案集 D D D中并不存在的虚拟的最佳方案,它的每个属性值都是决策矩阵中该属性的最优值;而负理想解 C 0 C^0 C0则是虚拟的最差方案,它的每个属性值都是决策矩阵中该属性的最差值。在 n n n为空间中,将方案集 D D D中的各备选方案 d i d_i di与正理想解 C ∗ C^* C∗和负理想解 C 0 C^0 C0的距离进行比较,既靠近正理想解又原理负理想解的方案就是方案集 D D D中的最优方案;并可以据此排定方案集 D D D中各备选方案的优先序。
理想解法关键在于属性空间定义适当的距离测度,就能计算备选方案与理想解的距离。TOPSIS法使用的是欧几里得距离。至于选择正理想解又用负理想解的原因在于有时会出现某两个备选方案与正理想解的距离相同的情况,为了区分这两个方案的优劣,引入负理想解并计算这两个方案与负理想解的距离,与正理想解的距离相同的方案离负理想解远者为优。
TOPSIS法的算法步骤
1、用向量规范化的方法求你的规范决策矩阵。设多属性决策问题的决策矩阵 A = ( a i j ) m ∗ n A=(a_ij)_m*_n A=(aij)m∗n,规范化决策矩阵 B = ( b i j ) m ∗ n B=(b_ij)_m*_n B=(bij)m∗n。
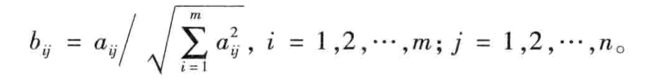
2、构造加权规范阵 C = ( c i j ) m ∗ n C=(c_ij)_m*_n C=(cij)m∗n。设由决策人给定各属性的权重向量为 w = [ w 1 , w 2 , . . . w n ] T w=[w_1,w_2,...w_n]^T w=[w1,w2,...wn]T,则:
c i j = w j ∗ b i j , i = 1 , 2 , . . . , m ; j = 1 , 2 , . . . , n c_ij=w_j*b_ij,i=1,2,...,m;j=1,2,...,n cij=wj∗bij,i=1,2,...,m;j=1,2,...,n
3、确定正理想解 C ∗ C^* C∗和负理想解 C 0 C^0 C0。设正理想解 C ∗ C^* C∗的第 j j j个属性值为 c j ∗ c_j^* cj∗,负理想解 C 0 C^0 C0第 j j j个属性值为 c i j 0 c_ij^0 cij0,则:

4、计算个方案到正理想解与负理想解的距离。备选方案 d i d_i di到正理想解的距离为:
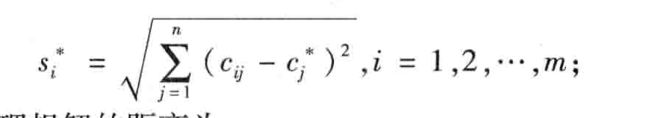
备选方案 d i d_i di到负理想解的距离为:
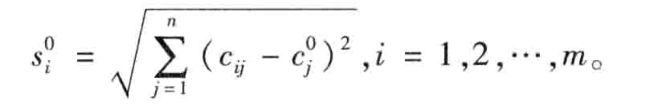
5、计算个方案对的排序指标值(即:综合评价指数),即:
f i ∗ = s i 0 / ( s i 0 + s i ∗ ) , i = 1 , 2 , . . . m f_i^*=s_i^0/(s_i^0+s_i^*),i=1,2,...m fi∗=si0/(si0+si∗),i=1,2,...m。
6、按 f i ∗ f_i^* fi∗由由大到小排列方案的优劣次序。
例题
P370-374
具体解析:
第一步:数据预处理。
数据预处理又称为属性值的规范化。
属性值具有多种类型,包括效益型、成本型和区间型等。这三种属性,效益型属性越大越好,成本型属性越小越好,区间型属性是在某个区间最佳。
在进行决策时,一般要进行属性值的规范化,主要有如下三个作用:1、属性值有多种类型,因此需要对数据进行预处理,使得表中任一属性下性能越优的方案变换后的属性值越大。2、非量纲化。属性值表中的每一列数具有不同的单位(量纲)。因此在用各种多属性决策方法进行分析评价时,需要排除量纲的选用对决策或评估结果的影响,这就是非量纲化。3、归一化。属性值表中不同指标的属性值数值大小差别很大,为了直观,更为了便于采用各种多属性决策与评估方法进行评价,需要把属性值表中的数值归一化,即把表中数值均变换到 [ 0 , 1 ] [0,1] [0,1]区间上。
此外,还可以在属性规范时用非线性变换或其它方法,来解决或部分解决某些目标的达到程度与属性值之间的非线性关系,以及目标间的不完全补偿性。

(2)标准0-1变换。为了使每个属性变换后的最优值为1且最差值为0,可以进行标准0-1变换。对效益型属性 x j x_j xj,令:
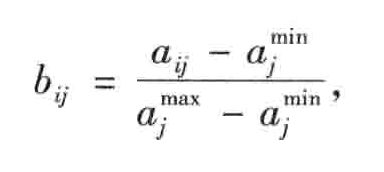
对成本型属性 x j x_j xj,令:
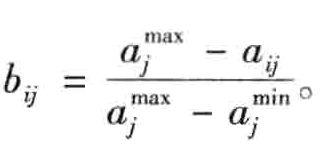
3、区间型属性的变换,有些属性既非效益型又非成本型。显然这种属性不能采用前面介绍的两种方法处理。

针对本题中的生师比,是采用上述函数来实现:
clc,clear
x2=@(qujian,lb,ub,x)(1-qujian(1)-x)./(qujian(1)-lb)).*(x>=lb & x=qujian(1) & x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*...
(x>qujian(2) & x<=ub);%定义变换的匿名函数
qujian=[5,6];lb=2,ub=12;%最优区间,无法容忍上界和下界
x2data=[5,6,7,10,2]';%x2属性值
y2=x2(qujian,lb,ub,x2data);%调用匿名函数,进行数据变换
4、向量规范化
向量规范化一般用下式进行变换:

该方法虽然应用广泛,但是从变换后的属性值大小仍然无法判断属性值的优劣。因为它的最大特点是,在规范化后,各方案的同一属性值的平方和为1。因此常用于计算各方案与某种虚拟方案(如:理想点或负理想点)的欧式距离。
5、标准化处理
该方法是为了消除变量的量纲效应,每个变量都有同等的表现力。数据分析中常对数据进行标准化的处理:
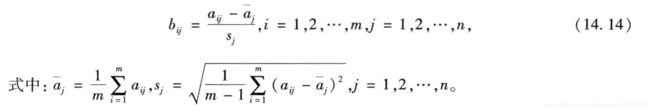
至此,本题的完整思路已经浮出水面:
1、相对数据进行标准化(通常使用z-score法);
2、然后针对具体的问题进行属性的区间变换;
3、再对向量进行规范化;
4、计算得到各个属性下的加权矩阵;
5、求解得到正理想解和负理想解,要分属性的类型来计算;
6、计算指标,并进行优劣排序。
以下是TOPSIS法的函数
function [ sf,ind ] = TOPSIS(AA,W)
%A为决策矩阵,W为权值矩阵,M为正指标所在的列,N为负指标所在的列
%该函数未进行区间类属性值的变换,因此需要使用者自行添加
[ma,na]=size(AA); %ma为A矩阵的行数,na为A矩阵的列数
%% 此处添加针对于区间型属性的属性变换
%% 下面是欧氏距离的计算
for j=1:na
A(:,j)=AA(:,j)/norm(AA(:,j));%向量的规范化
end
B=A.*repmat(W,ma,1);%求加权矩阵
Cstar=max(B);%求正理想解
C0=min(B);%求负理想解
for k=1:ma
Sstar(k)=norm(B(k,:)-Cstar);%求到正理想解的距离
S0(k)=norm(B(k,:)-C0);%求导负理想解的距离
end
f=S0./(Sstar+S0);
[sf,ind]=sort(f,'descend');%排序结果
参考文献
司守奎,孙玺菁. 数学建模算法与应用. 北京:国防工业出版社,2011.