通俗理解numpy.meshgrid()
先解释:生成网格点坐标矩阵
通俗理解:二维坐标下,形成的一个一个的网格点
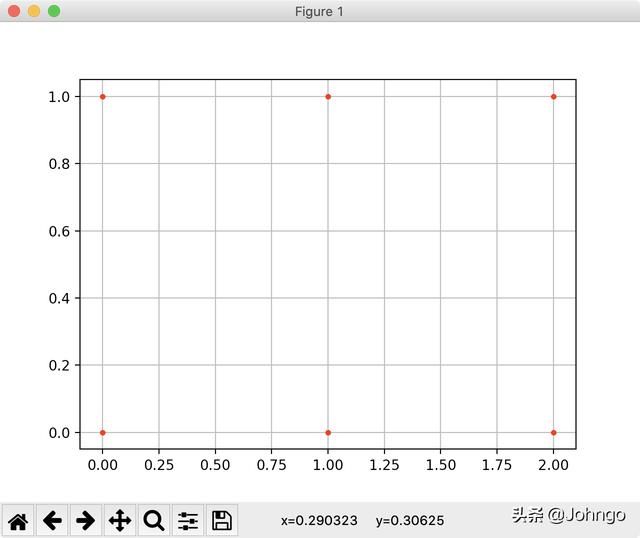
1.理解网格点, 6个点的图像
看到上述图中的点有 (0, 0,), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1)
那么,用矩阵或者二维数组表示为
>>> x = np.array([[0, 1, 2], [0, 1, 2]])
>>> y = np.array([[0, 0, 0], [1, 1, 1]])
>>> x
array([[0, 1, 2],
[0, 1, 2]])
>>> y
array([[0, 0, 0],
[1, 1, 1]])
需要完整的6个点,描述了一副坐标图,下面是完整的代码:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[0, 1, 2], [0, 1, 2]])
y = np.array([[0, 0, 0], [1, 1, 1]])
plt.plot(x, y,
color='r', # 全部点设置为红色
marker='.', # 点的形状为圆点
linestyle='') # 线型为空,也即点与点之间不用线连接
plt.grid(True)
plt.show()在这里的plt.plot()中的参数可以自由调整,显示不同形式的图,也可以不加样式参数试一下
比如:
plt.plot(x, y,
marker='.', # 点的形状为圆点
markersize=10, # 点设置大一点,看着清楚
linestyle='-.') # 线型为点划线
# 不加样式参数
plt.plot(x, y)
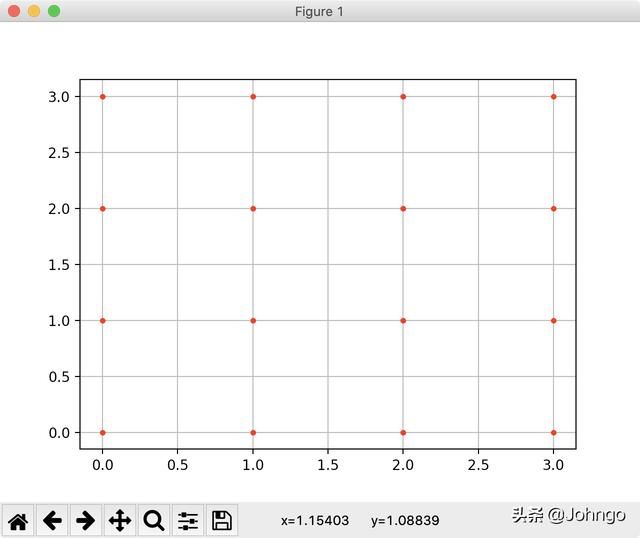
2.理解网格点, 16个点的图像
看下面的16个点的初始化设定,是不是感觉有点很多
代码:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3]])
y = np.array([[0, 0, 0, 0],
[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
plt.plot(x, y,
color='r', # 全部点设置为红色
marker='.', # 点的形状为圆点
linestyle='') # 线型为空,也即点与点之间不用线连接
plt.grid(True)
plt.show()那么, 如果网格点超级多呢,是不是还的一个又一个的都弄出来
这个时候就用到了numpy.meshgrid()方法
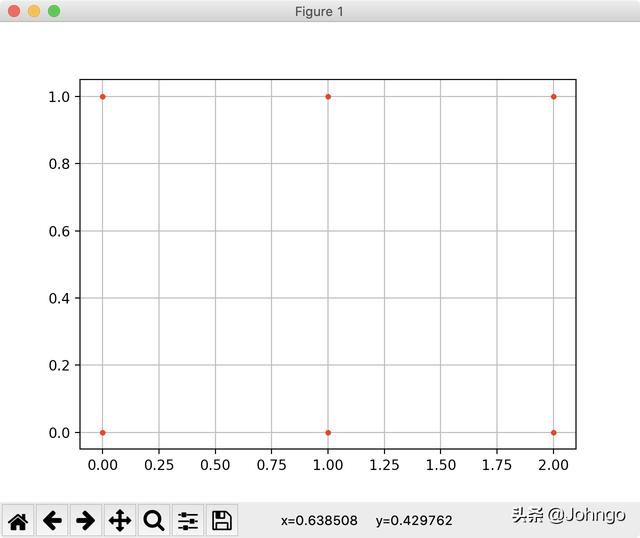
3.理解网格点,使用numpy.meshgrid()实现
基于网格点的规律性,可以使用numpy.meshgrid()直接生成想要的网格点就好了
还以二维平面举例:给定X轴和Y轴所有的点,将X和Y放到两个数组,进行笛卡尔乘积,从而得到所有的点。
举例:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0, 1, 2])
y = np.array([0, 1])
X, Y = np.meshgrid(x, y)
print(X)
print(Y)
plt.plot(X, Y,
color='red', # 全部点设置为红色
marker='.', # 点的形状为圆点
linestyle='') # 线型为空,也即点与点之间不用线连接
plt.grid(True)
plt.show()
是不是这样就很好理解了!
但是有一点,numpy.meshgrid()只能处理二维