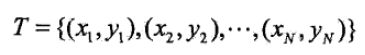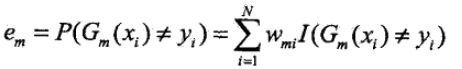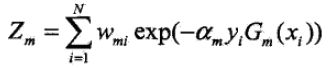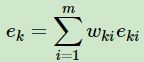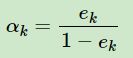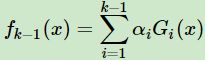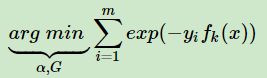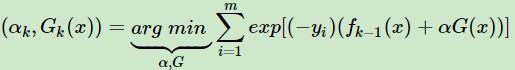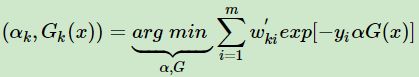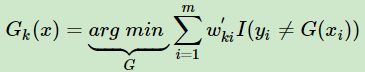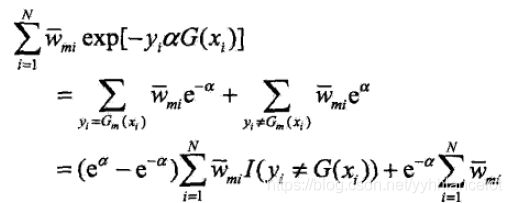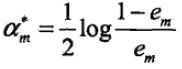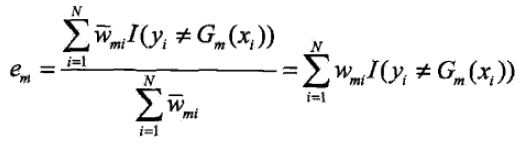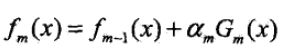个人总结：从随机森林(Bagging)到AdaBoost

众所周知，随机森林采用的是Bagging策略，关于随机森林与Bagging的一些知识，在个人总结：从决策树到随机森林中有所涉猎。

谈到bagging，就不得不联想到集成学习的另外一种方式，boosting。它和bagging的主要区别是，bagging是一种并行的方式，每个基学习器之前的依赖关系弱；而boosting是一种串行的方式，每个基学习器之间存在强依赖关系。

Boosting

Boosting意为提升，是一族可将弱学习器提升为强学习器的算法。Boosting方法训练基分类器时采用串行的方式，各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加，每一层在训练的时候，对前一层基分类器分错的样本，给予更高的权重。测试时，根据各层分类器的结果的加权得到最终结果。

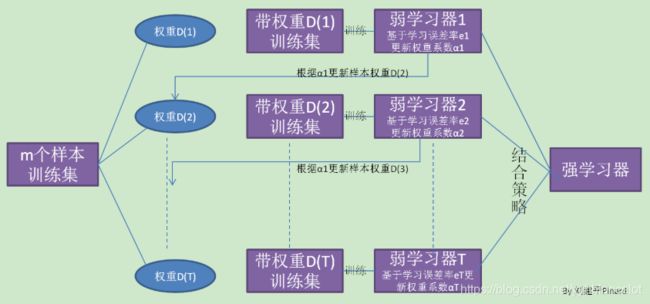
工作机制：先将训练集用初始权重训练出一个基学习器，再根据基学习器的训练误差率，使之前训练误差率高的点的权重变高，让其这些误差率高的点在后面的弱学习器中得到更多的重视，然后基于调整后的样本分布来训练下一个基学习器。如此重复直至基学习器的数量达到指定的T，最终将这T个弱学习器通过某种策略进行整合，得到最终的强学习器。

理论上任何学习器都可以用于AdaBoost，但一般来说，使用最广泛的AdaBoost弱学习器是决策树和神经网络。

Boosting代表：AdaBoost（Adaptive Boosting）

 

AdaBoost的分类

刚刚留下了四个问题：

1. 如何计算学习率误差
2. 如何得到弱学习器权重系数
3. 如何更新样本权重
4. 结合策略

AdaBoost的方案：

假设给定一个二类分类的训练集：，y为-1或+1

先初始化权值分布：

第一个问题，第m个弱分类器Gk(x)在训练集上的加权误差率为：

，这里w_mi为第m个分类器在第i个数据上的权重。

第二个问题，计算Gm(x)的系数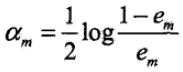，该对数为自然对数，这里要注意由于初始值权重w一般设为1/N，所以em肯定小于1。可以看出，em越接近1，alpha_m越小，这就意味着如果该分类器的误差率越大，对应的系数越小。当em为1时，alpha_m最小，为负无穷。

所以这时候有一个重要的插入步骤！当em>1/2时（误差率大于50%），break；要求em<= 1/2, 这保证了alpha_m的非负性！

第三个问题，更新样本权重。此时就有了第m+1个学习器的权重。

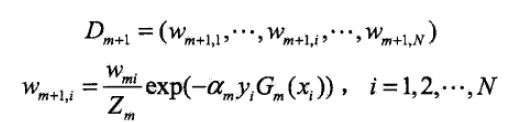，这里就可以看出，如果是正确分类的样本，exp内部就为负，下一个学习器对于该样本的权重就越小；相反如果是错误分类的样本，exp内部就为正，下一个权重就越大。

这里插入一下：在sklearn中只有AdaBoostClassifier有一个叫algorithm的参数，分别是SAMME和SAMME.R。它们的主要区别是弱学习器权重的度量，SAMME采用的就是上述的使用样本集分类效果作为弱学习器权重度量，而SAMME.R使用的是对样本集分类概率的大小作为权重度量。由于SAMME.R使用了概率的连续值，迭代会比SAMME更快。但是SAMME.R使用的基学习器必须能够是支持概率预测的分类器。而SAMME没有这个限制。sklearn中默认的是SAMME.R。

其中，Zm是规范化因子。

最后一个问题，集合策略。AdaBoost分类采用加权表决，最终的强分类器为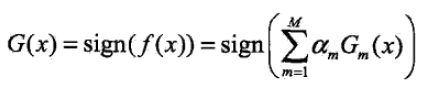

要记得每个弱分类器的输出为-1或1，最后是将所有的分类器的输出加权组合，再使用sign函数。

小结：所以这个时候回头看开始那张图，AdaBoost的本质在于每次更新训练集的权重，得到每次对应的alpha_m（样本权重——>弱分类器误差率——>弱分类器权重alpha）。AdaBoost本质上是一个加法模型，对样本分配不同的权重，计算误差率时使用这些权重，从而让“错分的样本权重越来越大，使它们更被重视。”

 

AdaBoost的回归

AdaBoost回归有很多变种，这里以AdaBoost R2算法为准。

对于第k个弱学习器，定义最大误差为

定义每个样本的相对误差为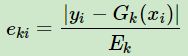，这是误差为线性的时候，对应为sklearn里AdaBoostRegressor的loss参数'linear'；如果定义为平方误差，则是，对应参数为'square'；如果是指数误差，则是，对应参数'exponential'。

最终得到第k个学习器的误差率。接着便是弱学习器权重系数。

更新样本权重，第k+1个弱学习器的样本集权重系数为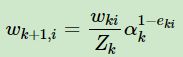，其中Zk为规范化因子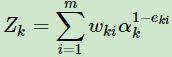

最终的强回归器为。

Gk*：对所有的alpha_k，取ln(1/alpha_k)，找到中位数对应的序号k，其对应的弱分类器就为Gk*。

小结：所以综上所述，AdaBoost回归的本质上还是求所有弱分类器对应的alpha值。AdaBoost用错分数据点来识别问题，调整错分数据点的权重来改进模型。

 

AdaBoost分类问题的损失函数优化

AdaBoost本质上是一个加法模型，一个前向分布学习算法，损失函数为指数函数的分类问题。

第k-1轮的强学习器为

第k轮的强学习器为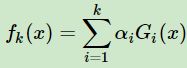，可知，可见强学习器确实是通过前向分布学习算法一步步而得到的。

由于损失函数为指数函数，则定义损失函数

由其与前向分布学习算法的关系，则可以得到损失函数为

令，该变量既不依赖alpha也不依赖G，则损失函数转化为

而对于任意alpha>0，

对alpha求导得到，其中

最后由，以及

可得，这就是只相差了规范化因子的样本权重更新公式。

AdaBoost算法的正则化

为了防止过拟合，加入正则化项，称为步长(learning rate)，定义为v。

在没加之前弱学习器的迭代

加了之后

v的取值范围为0

在sklearn中的解释为：Learning rate shrinks the contribution of each classifier.

AdaBoost小结

使用最广泛的AdaBoost弱学习器还是决策树和神经网络，对于决策树，AdaBoost分类使用CART分类树，回归则是CART回归树。

主要优点：

1、分类的精度很高

2、在该框架可以使用各种回归分类模型来构造弱学习器，非常灵活。

3、不易过拟合

主要缺点：

对异常样本敏感，异常样本在迭代中可能获得较高权重，最终影响强学习器的预测准确性。