数据结构（一） -- C语言版 -- 基本概念与算法基本概念

一、数据结构中的基本概念

1.1、数据

  也就是基本数据类型、构造数据类型

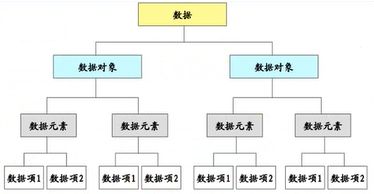
  数据：数据即信息的载体，是能够输入到计算机中并且能被计算机识别、存储和处理的符号总称，也是程序的操作对象，用于描述客观事务
  数据元素：是数据的基本单位，又称之为记录。一般由若干基本项（或称字段、域、属性）组成
  数据项 ：一个数据元素有若干个数据元素组成
  数据对象：性质相同的数据元素的集合

1.2、结构

  指数据之间的相互关系。下面简单进行说明。

1.2.1、逻辑结构

  是从具体问题中抽象出来的数学模型，主要有下面几种类型：
  线性结构：一个对一个，如线性表、栈、队列

  集合 ：数据元素间除“同属于一个集合”外，无其它关系

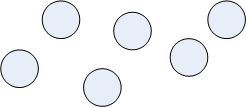
  树形结构：一个对多个，如树

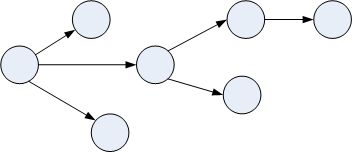
  图状结构：多个对多个，如图

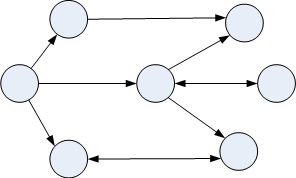
1.2.2、存储结构（物理结构）

  指的是数据的逻辑结构在计算机存储器中的映象（或表示），它是依赖于计算机
  顺序：借助元素在存储器中的相对位置来表示数据元素间的逻辑关系
  链式：借助指示元素存储地址的指针表示数据元素间的逻辑关系
  索引：在存储数据的同时，建立一个附加的索引表，即索引存储结构=数据文件+索引表
  散列：根据数据元素的特殊字段(称为关键字key)，计算数据元素的存放地址，然后数据元素按地址存放，所得到的存储结构为散列存储结构(或Hash结构，MD5，sha1，sha256，sha512，sm系列)

1.3、数据结构

  主要是研究非数值性程序设计中计算机操作的对象（数据）及其相互间关系和运算的学科。也可以简单理解为研究数据对象中数据元素之间的关系（数组、链表、树、图）

1.4、数据的运算

  即在数据的逻辑结构上已定义的操作,在数据的存储结构上实现。
  最常用的数据运算：插入、删除、修改、查找、排序
  数据结构总体可以简单归纳为如下图所示。

二、算法中的基本概念

2.1、算法的概述

  算法（Algorithm）是一个有穷规则（或语句、指令）的有序集合。它确定了解决某一问题的一个运算序列。对于问题的初始输入，通过算法有限步的运行，产生一个或多个输出。
  可以简单理解为：算法是特定问题的求解的步骤的描述。在计算机中表现为指令的有限序列。

2.2、算法的特性

  输入：0或者多个外部输入
  输出：至少一个外部输出
  有穷性：在执行有限的步骤之后会自动结束而不会无限循环
  确定性：每一步都有确定的含义
  可行性：每一步都是可行的、能够在有限的时间内完成

2.3、算法设计的要求

  正确性：算法需要满足具体问题的需求，并且对于精心选择的典型的，苛刻的机组输入数据能够得出满足规格说明的结果
  可读性：不同人员能够阅读、正确理解、交流
  健壮性：对于各种合法或者不合法的输入，能够合法、适当地做出反应或者进行处理
  效率和低存储量需求：执行需要的时间、需要的最大的存储空间。

2.4、算法和数据结构的关系和区别

2.4.1、关系

  算法设计: 取决于选定的逻辑结构
  算法实现: 依赖于采用的存储结构

2.4.2、区别

  数据结构只是静态的描述了数据元素之间的关系，高效的程序需要在数据结构的基础上设计和选择算法 --> 程序 = 算法 + 数据结构
  所以总结如下。

• 算法是为了解决实际问题而设计的
• 数据结构是算凡需要处理的问题载体
• 数据结构与算法是相辅相成的

2.5、算法的效率复杂度，也称为算法的时间复杂度

2.5.1、事后统计法

  比较不同算法对同一组输入数据的运行处理时间
缺陷：

• 为了获得不同算法的运行时间必须编写相应的程序
• 运行时间严重依赖于硬件、运行环境等因素
• 算法的测试数据的选取比较困难

2.5.2、事前分析估算

  依据统计的方法对算法效率进行估算。
  ①、主要注意的是：

• 计算一个算法的效率时，只需要关注操作数量是我最高次项，其他的次要项和常数项可以省略
• 在没有特殊说明时，所分析的算法的时间复杂度都是在最坏的情况下的时间复杂度

  ②、影响算法的主要因素

• 算法采用的策略和方法
• 问题的输入规模
• 编译器所产生的代码
• 计算机执行的速度

  以下面的加和的程序为例：

#include 

long sum1(int n)
{
     
    long ret = 0; //时间复杂度 -- 1步   空间复杂度 -- 4字节
    int *array = (int *)malloc(n * sizeof(int)); //时间复杂度 -- 1步   空间复杂度 -- 4 * n字节
    int i; // 1步  空间复杂度 -- 4字节
    for (i = 0; i < n; i++) //时间复杂度 -- n步  空间复杂度 -- 0字节
    {
     
        array[i] = i + 1;
    }
    for (i = 0; i < n; i++) //时间复杂度 -- n步    空间复杂度 -- 0字节
    {
     
        ret += array[i];
    }
    free(array); //时间复杂度 -- 1步    空间复杂度 -- 0字节
    return ret;
}
long sum2(int n)
{
     
    int ret = 0; //时间复杂度 -- 1步    空间复杂度 -- 4字节
    int i; //时间复杂度 -- 1步   4字节
    for (i = 0; i < n; i++) //时间复杂度 -- n步   空间复杂度 -- 0字节
    {
     
        ret += i + 1;
    }
    return ret;
}

long sum3(int n)
{
     
    int ret = 0; //时间复杂度 -- 1步   空间复杂度 -- 4字节
    if (n > 0)
    {
     
        ret = (1 + n) * n / 2; //时间复杂度 -- 1步    空间复杂度 -- 0字节
    }
    return ret;
}

int main(int argc, const char *argv[])
{
     
    printf("sum = %d\n", sum1(100));
    printf("sum = %d\n", sum2(100));
    printf("sum = %d\n", sum3(100));
    return 0;
}

  就与上述的代码，通过具体的n的步骤的多少就可以推导出算法的复杂度，其中sum1函数的加和的算法，其总共需要的步数为 2n + 3， sum2函数的步数为n+2，sum3函数中，公式 ret = (1+n)*n/2 的步数可以简单认为1步，或者2步，总归sum3的步数为常量级。
  所以，用大O表示法来计算，在n趋近于无穷大的时候，则sum1函数的时间复杂度为O(n)，sum2为O(n)，sum3的为O(1)。
  常見的时间复杂度入下图所示（图片摘自《大话数据结构》）：

  常用的时间复杂度所耗费的时间从此小到大依次入下图所示（图片摘自《大话数据结构》）。

2.6、算法的空间复杂度

  通过计算算法的对于内存的需求，计算存储空间的实现。
  在上面的代码中，sum1的空间复杂度为 4n+8，sum2的空间复杂度为8，sum3的空间复杂度为 4。
  所以，用大O表示法来计算，在n趋近于无穷大的时候，则sum1函数的空间复杂度为O(n)，sum2为O(1)，sum3的为O(1)。

2.7、用空间换时间的思路

  以下面的问题为例子进行简单的说明：

问题描述：
  在一个有自然数1 - 1000中某些数字组成的数组中，每个数字可能出现0次或者多次，设计一个算法程序，找出出现次数最多的数字。
解题思路：

  数字n出现的次数，放在新开的内存空间 a[n-1] 位置上。把每一个数字的中间结果都给缓存下来。这种情况，用新开辟的内存空间来缓存中间结果，在需要这个中间结果的时候，直接拿出来使用，减少复杂的计算以节省时间。
  1、创建一个新的临时数组，用于存储运算过程中的中间结果
  2、遍历原数组，求出每一个数字出现的次数，然后记录到临时数组中
  3、扫描临时数组，求出最大数
  4、最大数的值即为出现次数最多的数字的索引值，+1则为出现次数最多的数字

  代码示例：

#include 

void serch(int buf[], int len)
{
     
    int tmp[1024] = {
     0};
    int i = 0, max = 0;

    for (i = 0; i < len; i++) // 遍历原数组，求出每一个数字出现的次数，然后记录到临时数组中
    {
     
        int index = buf[i] - 1;
        tmp[index] += 1;
    }

    for (i = 0; i < 1000; i++) // 扫描临时数组，求出最大数
    {
     
        if (max < tmp[i])
        {
     
            max = tmp[i];
        }
    }

    for (i = 0; i < 1000; i++) // 打印最大数
    {
     
        if (max == tmp[i])
        {
     
            printf("The num is : %d\n", i++);
        }
    }
}

int main(int argc, const char *argv[])
{
     
    int array[] = {
     1, 2, 3, 4, 3, 4, 5, 6, 7, 3, 3, 2, 1, 8, 9, 3, 4, 7, 9};
    serch(array, sizeof(array) / sizeof(*array));
    return 0;
}

上一篇：无
下一篇：数据结构（二） – C语言版 – 线性表的顺序存储