LDA主题模型
LDA(Latent Dirichlet Allocation)是一种文档主题生成模型,这个模型包含了词、主题和文档三层结构。所谓的生成模型,就是说我们人为一篇文章的每个词都是通过 “以一定概率选择了某个主题,并从这个主题中以一定的概率选择某个词语” 的这样的一个过程得到的。其中,词、主题和文档的关系就是文档到主题服从多项式分布,主题到词也服从多项式分布。
首先,我们直观地看一下 LDA 模型,比如一个企业招聘,有很多应聘者投来了简历,那么公司的HR怎么通过简历来判断应聘者的优劣呢?在简历中往往会包含应聘者的特征,那么这些特征就可以来给HR描述一个应聘者的形象,然后HR通过这些特征描述出来的应聘者形象可以判断这名应聘者的优劣,如下图所示就是特征词描述的一个应聘者形象:

通过简历上的一些特征词,就可以描述一个应聘者的形象,从 “秃头”、“格子衬衫” 这样的词语就大概率可以看出来这是一名优秀的程序员,然后我们通过这些特征词语描述的应聘者的形象来分析这名应聘者的优劣,整个过程如下图所示:

这就是一个直观的 LDA 流程,HR 是通过一个个特征词的组合,来在自己的脑海里构建此应聘者的形象,就可以评判这个应聘者优劣的概率各自是多少。我们以此来看看 LDA 和简历应聘者之间的关系如何,如下图所示:

我们很容易应聘者的案例的流程,那么 LDA 模型可以类似地引申出来,就是应聘者的特征就是 LDA 模型中的单词,单词组成了文档,就相当于是特征组成了简历,我们再来通过构建出来的文档来通过概率模型猜测这篇文章的主题,当然,这个模型是一个词袋模型,我们将这些词放在一个袋子中,没有顺序可言,我们通过袋子中的词,来猜测这篇文章的主题。这么一说,我们就可以直观地感受到 LDA 主题模型的大概意思和每个组成部分之间的关系了。
有了直观的理解之后,我们可以从数学的角度来看看 LDA 模型,根据标准的贝叶斯公式,我么可以得到: P ( 单词|文档 ) = P ( 单词|主题 ) * P ( 主题|文档 ) P({\text{单词|文档}}){\text{ = }}P({\text{单词|主题}}){\text{*}}P({\text{主题|文档}}) P(单词|文档) = P(单词|主题)*P(主题|文档)
也就是说在文档中出现某个单词的概率等于某个主题中出现这个单词的概率乘以文档中出现这个主题的概率,因为在这个公式中主题这个信息在相乘的过程中消除了,在外部看来没有主题这个信息,所以主题是一个隐变量,所以用 latent 修饰。有了上述这些基础,我们就可以得到 LDA 生成的过程:
- 对每一篇文章,从主题分布中抽取一个主题;
- 从上述被抽到的主题所对应的单词分布中抽取一个单词;
- 重复上述的过程直至遍历文档中的每一个单词。
为了说明上述的过程,我们需要知道几个数学的知识,首先是伽马函数,伽马函数其实就是阶乘函数在实数上的推广,对于整数来说, Γ ( n ) = ( n − 1 ) ! \Gamma (n) = (n - 1)! Γ(n)=(n−1)!对于实数来说: Γ ( x ) = ∫ 0 ∞ t x − 1 e − t d t \Gamma (x) = \int\limits_0^\infty { {t^{x - 1}}{e^{ - t}}dt} Γ(x)=0∫∞tx−1e−tdt
然后就是二项分布,二项分布是从伯努利分布演化而来的,伯努利分布又称0-1分布,是一个离散型的随机分布,其中的随机变量只有两类取值,正和负两类 {+,-},而二项分布就是重复 n 次的伯努利实验,重复做了 n 次,是二项分布;那么二项分布的概率密度函数是: P ( K = k ) = C k n p k ( 1 − p ) n − k P(K = k) = C_k^n{p^k}{(1 - p)^{n - k}} P(K=k)=Cknpk(1−p)n−k
第三就是多项分布,是二项分布扩展到多维的情况,也就是说多项分布的随机变量取值不再是0和1,扩展到多维的情况就是有多种的离散值可能 ( 1 , 2 , 3 , . . . , k ) (1,2,3,...,k) (1,2,3,...,k),这些值的可能性相加起来的概率总和为1,那么多项分布的概率密度函数为:
P ( x 1 , x 2 , . . . , x k ; n , p 1 , p 2 , . . . , p k ) = n ! x 1 ! . . . x k ! p 1 x 1 . . . p k x k P({x_1},{x_2},...,{x_k};n,{p_1},{p_2},...,{p_k}) = \frac{ {n!}}{ { {x_1}!...{x_k}!}}p_1^{ {x_1}}...p_k^{ {x_k}} P(x1,x2,...,xk;n,p1,p2,...,pk)=x1!...xk!n!p1x1...pkxk
第四个是贝塔分布,这是一个二项分布的共轭先验分布,贝塔分布就是给定参数 α > 0 \alpha > 0 α>0, β > 0 \beta > 0 β>0,取值范围是 [ 0 , 1 ] [0,1] [0,1] 的随机变量 x x x 的概率密度函数:
f ( x ; α , β ) = 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 f(x;\alpha ,\beta ) = \frac{1}{ {B(\alpha ,\beta )}}{x^{\alpha - 1}}{(1 - x)^{\beta - 1}} f(x;α,β)=B(α,β)1xα−1(1−x)β−1
其中:
1 B ( α , β ) = Γ ( α + β ) Γ ( α ) Γ ( β ) \frac{1}{ {B(\alpha ,\beta )}} = \frac{ {\Gamma (\alpha + \beta )}}{ {\Gamma (\alpha )\Gamma (\beta )}} B(α,β)1=Γ(α)Γ(β)Γ(α+β)
最后是我们的狄利克雷(Drichlet)分布,这个是贝塔分布在高纬度上面的推广,公式如下:
f ( x 1 , x 2 , . . . , x k ) = 1 B ( α ) ∏ i = 1 k x i α i − 1 f({x_1},{x_2},...,{x_k}) = \frac{1}{ {B(\alpha )}}\prod\limits_{i = 1}^k {x_i^{ {\alpha ^i} - 1}} f(x1,x2,...,xk)=B(α)1i=1∏kxiαi−1
其中:
B ( α ) = ∏ i = 1 k Γ ( α i ) Γ ( ∑ i = 1 k α i ) , ∑ x i = 1 B(\alpha ) = \frac{ {\prod\limits_{i = 1}^k {\Gamma ({\alpha ^i})} }}{ {\Gamma (\sum\limits_{i = 1}^k { {\alpha ^i}} )}},\sum { {x_i} = 1} B(α)=Γ(i=1∑kαi)i=1∏kΓ(αi),∑xi=1
说完了分布,我们再来看看几个主题模型:
首先是 Unigram model:
对于文档 W = ( w 1 , w 2 , . . . , w N ) W = ({w_1},{w_2},...,{w_N}) W=(w1,w2,...,wN),那么用 p ( w n ) p({w_n}) p(wn) 表示词 w n w_n wn 的先验概率,生成文档 W W W 的概率为:
p ( W ) = ∏ n = 1 N p ( w n ) p(W) = \prod\limits_{n = 1}^N {p({w_n})} p(W)=n=1∏Np(wn)
也就是说一篇文档由 n n n 个词,每个词出现的概率是 p ( w k ) p({w_k}) p(wk),那么将每个词的出现概率相乘就可以得到这篇文档出现的概率,比较容易理解。
然后是 Mixture of unigram model
这个模型生成的过程如下:
- 首先按照某种分布给某个文档选择一个主题 z z z。
- 再根据该主题生成文档,那么这个文档中所有的词都来自一个主题 z z z。
假设主题有 z 1 , z 2 , z 3 , . . . , z k z_1,z_2,z_3,...,z_k z1,z2,z3,...,zk,那么生成文档的概率为:
p ( W ) = p ( z 1 ) ∏ n = 1 N p ( w n ∣ z 1 ) + . . . + p ( z k ) ∏ n = 1 N p ( w n ∣ z k ) = ∑ z p ( z ) ∏ n = 1 N p ( w n ∣ z ) p(W) = p({z_1})\prod\limits_{n = 1}^N {p({w_n}|{z_1})} + ... + p({z_k})\prod\limits_{n = 1}^N {p({w_n}|{z_k})} = \sum\limits_z {p(z)\prod\limits_{n = 1}^N {p({w_n}|z)} } p(W)=p(z1)n=1∏Np(wn∣z1)+...+p(zk)n=1∏Np(wn∣zk)=z∑p(z)n=1∏Np(wn∣z)
有了这两个模型,我们就可以引申出进阶版的模型PLSA model:
在上述的 Mixture of unigram model 中,我们只给每一篇文章一个主题,但是实际的事例中,一篇文章可能会有几个主题,每个主题出现的概率不一样,整个模型的示意图如下所示:
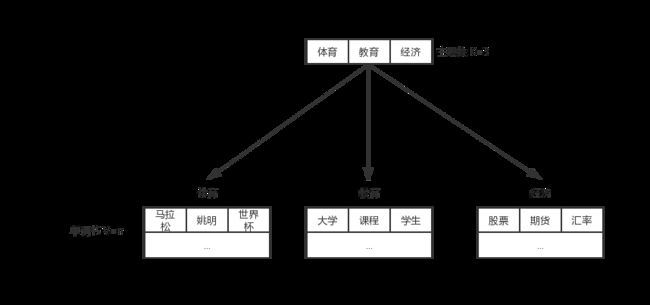
假设我们有体育、教育和经济三个主题,我们首先按照某种分布选择一个主题,然后从这个主题所对应的词中按照某种分布选择词语组成文档。那么通过观测可以得到 “知道文档主题是什么,就用什么单词”,那么我们反过来推导就是 “看到了什么单词,就知道文档的主题是什么”。这样我们就可以根据大量已知的 文档 - 词 的概率 P ( w j ∣ d i ) P(w_j|d_i) P(wj∣di),训练出 文档 - 主题 P ( z k ∣ d i ) P(z_k|d_i) P(zk∣di) 和 主题 - 词 P ( w j ∣ z k ) P(w_j|z_k) P(wj∣zk),可以用下面的公式表示:
P ( w j ∣ d i ) = ∑ k = 1 K P ( w j ∣ z k ) P ( z k ∣ d i ) P({w_j}|{d_i}) = \sum\limits_{k = 1}^K {P({w_j}|{z_k})P({z_k}|{d_i})} P(wj∣di)=k=1∑KP(wj∣zk)P(zk∣di)
这个很好理解,一共有 K K K 个主题,把每个主题下出现词 w i w_i wi 的概率乘以第 i i i 个文档情况下出现主题 z k z_k zk 的概率再求和,就可以得到文档 d i d_i di 出现 词 w j w_j wj 的概率,由此还可以得到文档中每个词的生成概率为:
P ( d i , w j ) = P ( d i ) P ( w j ∣ d i ) = P ( d i ) ∑ k = 1 K P ( w j ∣ z k ) P ( z k ∣ d i ) P({d_i},{w_j}) = P({d_i})P({w_j}|{d_i}) = P({d_i})\sum\limits_{k = 1}^K {P({w_j}|{z_k})P({z_k}|{d_i})} P(di,wj)=P(di)P(wj∣di)=P(di)k=1∑KP(wj∣zk)P(zk∣di)
因为 P ( d i ) P(d_i) P(di) 是先验概率可以事先求得, P ( w j ∣ z k ) P(w_j|z_k) P(wj∣zk) 和 P ( z k ∣ d i ) P(z_k|d_i) P(zk∣di) 是未知的,那么 θ = ( P ( w j ∣ z k ) , P ( z k ∣ d i ) ) \theta = (P({w_j}|{z_k}),P({z_k}|{d_i})) θ=(P(wj∣zk),P(zk∣di)) 就是我们需要估计的参数,我们的任务就是要最大化这个 θ \theta θ。
那么最后就是我们的 LDA model 就是在 P L S A PLSA PLSA 模型的基础上加上一层贝叶斯框架,也就是说 LDA 模型就是 PLSA 的贝叶斯版本,也就是在随机抽取主题和词的过程是服从 狄利克雷 分布的。这就是从数学的角度解释了 LDA 模型,总的来说,LDA 是一种典型的词袋模型,也就是说一篇文档是由一组词构成的一个集合,每个词之间是没有顺序关系的。一篇文档可以包含多个主题,文档中的每一个词都是由其中的一个主题生成的。
为了更加直观地表示 PLSA 和 LDA 的区别,我们来看看这两种模型生成文档的不同过程示意图:
PLSA:

从示意图中我们可以得到我们先选择一篇文章 d,然后按照 P ( 主 题 ∣ 文 档 ) P(主题|文档) P(主题∣文档) 选择文档隐含的主题 z,确定了主题之后然后确定词分布,按照 P ( 词 ∣ 主 题 ) P(词|主题) P(词∣主题) 的概率来选择词 w。
LDA:
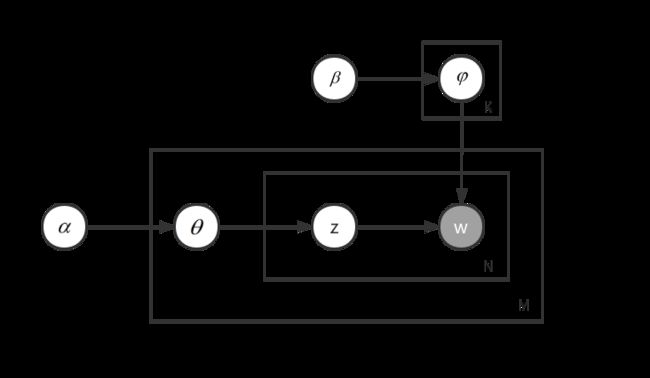
由上图可知,先要按照先验概率 P ( d i ) P(d_i) P(di) 选择一篇文档 d i d_i di,然后通过狄利克雷分布 α \alpha α 中取出生成文档 d i d_i di 的主题分布 θ i \theta_i θi,有了 θ i \theta_i θi 之后,我们就可以从中取出文档 d i d_i di 的第 j 个词的主题 z i , j {z_{i,j}} zi,j,然后从狄利克雷分布 β \beta β 中取样生成主题 z i , j {z_{i,j}} zi,j 对应的词语分布 φ z i , j {\varphi _{ {z_{i,j}}}} φzi,j,最后从词语多项式分布 φ z i , j {\varphi _{ {z_{i,j}}}} φzi,j 中采样最终生成词语 w i , j w_{i,j} wi,j,这就是 LDA 生成文档的过程。这两个模型的区别也就是 LDA 模型在 PLSA 模型的基础上对主题分布和词分布加上了两个狄利克雷先验。
讲到这里,LDA 模型我们就讲完了,希望可以帮助大家更深层次地理解 LDA 主题模型,谢谢。