STM32 电机教程 16 - PMSM电机磁场定向控制原理

前言

磁场定向控制又称矢量控制（FOC）, 本质上为控制定子电流的幅度和相位，使之产生的磁场和转子的磁场正交，以产生最大的扭矩.

1. PMSM 的磁场定向控制

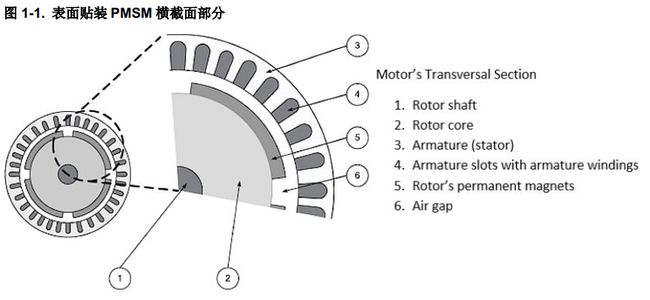
磁场定向控制（ Field Oriented Control， FOC）表示这样一种方法：将其中一个磁通（转子、定子或气隙）视为所有其他量的参考坐标系，其目的是将定子电流解耦为用于产生转矩的分量和用于产生磁通的分量。这种解耦保证了复杂三相电机的控制方式与采用单独励磁的直流电机一样简单。这意味着电枢电流负责产生转矩，而励磁电流负责产生磁通。在本文档中，将转子磁通视为参考坐标系。PMSM 的气隙磁通是平滑的，反电动势（ Back Electromotive Force， BEMF）是正弦曲线。提出的控制方案已开发用于表面贴装式永磁同步电机。下图所示为表面贴装电机，与内置式 PMSM 相比，该电机具有低转矩纹波和低成本的优点

表面安装永磁型 PMSM（ SPM）中 FOC 的特殊性在于定子（对应于电枢反应磁通）的 d 轴电流参考idref设置为零。转子中的磁体产生转子磁链 ψm，这一点与交流感应电机（ AC Induction Motor， ACIM）不同，后者需要正 idref 来生成磁化电流，从而产生转子磁链。气隙磁通是定子和转子磁链的总和。在 PMSM 中，转子磁链由永磁体产生，定子磁链（电枢反应磁链）由定子电流产生。在 FOC 中，如果低于额定速度，则不会产生定子磁链，因为“id”设置为零，因此气隙磁通仅等于 ψm。如果高于额定速度，“id”设置为负值，定子磁链与 ψm 相对，进而会减弱气隙磁通。FOC 可使用速度传感器或无速度传感器方法实现。对于高精度控制应用，首选有传感器的控制。在有传感器的 FOC 实现中，使用编码器或解析器确定转子位置和机械速度。本应用笔记介绍了本文档中基于编码器的实现。

2. PMSM 有传感器 FOC 的框图

控制过程总结如下：

• 测量三相定子电流。对于具有平衡三相绕组的电机，只需测量两个电流即可。第三个电流可使用以下公式计算得出：

公式计算得出：

• 将三相电流转换到静止双轴系统。该转换通过测量的 ia、 ib 和 ic 值提供 iα 和 iβ 变量。从定子的角度来看，值 iα 和 iβ 是随时间变化的正交电流值。

• 使用在控制环最后一次迭代时测量的变换角度旋转静止双轴坐标系，以与转子磁通对准。该转换通过iα 和 iβ 提供 id 和 iq 变量。值 id 和 iq 是变换到旋转坐标系的正交电流。对于稳态条件， id 和 iq 恒定。

• 电流参考值的说明如下：

– id 参考：控制转子磁通

– iq 参考：控制电机转矩输出

• 将误差信号馈入到 PI 控制器。控制器的输出提供 vd 和 vq，它们是将施加到电机上的电压向量。

• 新的变换角度通过编码器脉冲输入测得。这一新角度将指导 FOC 算法确定放置下一个电压向量的位置。

• 使用新的角度将来自 PI 控制器的 vd 和 vq 输出值旋转回静止参考坐标系。该计算可提供下一个正交电压值 vα 和 vβ。

• vα 和 vβ 值用于计算生成所需电压向量所用的全新 PWM 占空比值

• 在每个离散 PWM 周期后都会计算机械速度（ ωm）

 

在数据转换结束后， FOC 软件在 ADC 中断服务程序中实现。其运行速率与 PWM 开关频率相同。

 

PMSM 的磁场定向控制框图如下图所示。

 

4. PID 控制器

4.1 PID 控制器背景

比例积分微分（ Proportional Integral Derivative， PID）控制器的完整说明已超出本文档范围。不过，本节提供了 PID 操作的一些基础知识。

 

PID 控制器在闭合控制环中响应误差信号，并尝试调节控制量以实现所需的系统响应。受控参数可以是任何可测量的系统量，例如速度或磁通。 PID 控制器的优势在于，可以通过改变一个或多个增益值并观察系统响应的变化来凭经验进行调节。

以周期性采样间隔执行数字 PID 控制器。假设控制器频繁执行，因此可以控制系统。通过从要控制参数的实际测量值中减去该参数的预期设置来得到误差信号。误差符号表示控制输入所需的更改方向。

 

控制器的比例（ P）项通过将误差信号乘以“P”增益得到，这会使 PID 控制器产生控制响应，此响应是误差幅值的函数。随着误差信号变大，控制器的“P”项会变大，进而实现进一步校正。

 

“P”项的作用是随着时间的推移减小总体误差。不过，误差接近零时，“P”项的作用将减小。在大多数系统中，受控参数的误差非常接近于零，但不会收敛。因此，最终会有一个较小的剩余稳态误差。

 

控制器的积分（ I）项用于消除这个小稳态误差。“I”项计算连续运行的误差信号总和。因此，小稳态误差随时间累积成大误差值。此累积误差信号与“I”增益因子相乘，成为 PID 控制器的“I”输出项。PID 控制器的差分（ D）项用于提高控制器的速度并响应误差信号的变化率。通过从先前值减去当前误差值计算得出“D”项输入。此增量误差值与“D”增益因子相乘，成为

 

PID 控制器的“D”输出项。当系统误差快速变化时，控制器的“D”项会产生更多的控制输出。并非所有控制器都会实现“D”或“I”项（不常用）。例如，此应用不使用“D”项，因为它会放大噪声，这反过来会导致 PWM 占空比发生过度变化，从而影响算法的工作并产生过电流跳闸。

 

4.2 调整 PID 增益

 

PID 控制器的“P”增益用于设置整体系统响应。要调整 PID 控制器，请将“I”和“D”增益设置为零。然后，增大“P”增益，直到系统响应设定值变化，且无过多过冲或振荡。如果使用的“P”增益值较小，则以缓慢方式控制系统；如果使用的值较大，则会实现积极控制。现在系统可能不会收敛到设定值。

 

选择完合理的“P”增益后，慢慢增大“I”增益以强制系统误差为零。在大多数系统中只需要较小的“I”增益。如果“I”增益足够大，则其作用可以克服“P”项的作用、减慢整体控制响应速度并使系统在设定值处上下振荡。如果发生振荡，减小“I”增益并增大“P”增益通常可以解决此问题。

 

此应用包括一个用于限制积分饱和的项，如果积分误差使输出参数饱和，则会出现该项。积分误差的任何进一步增大都不会影响输出。累积误差在减小时，必须下降（或回退）到低于导致输出饱和的值。“Kc”系数会限制这种不必要的累积。对于大多数情况，该系数可以设置为等于“Ki”。

 

4.3 FOC 中的控制环

 

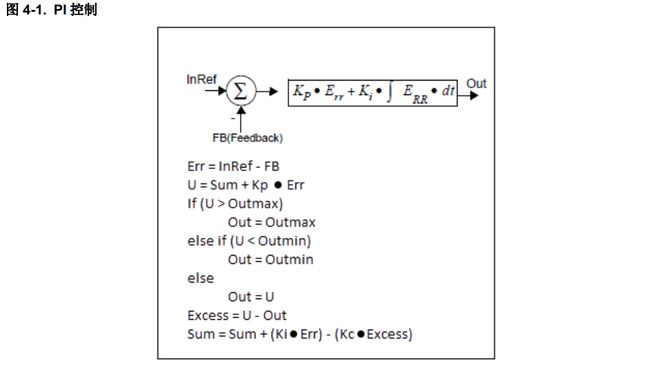
三个 PI 环用于独立控制三个交互变量。转子速度、转子磁通和转子转矩分别由单独的 PI 控制器模块控制。这是一种传统实现，其中包含限制积分饱和的项（ Kc.Excess），如下图所示。 Excess 通过无限制输出（ U）减去有限制输出（ Out）计算而得。项 Kc 与 Excess 相乘，限制累积的积分部分（ Sum）。

 

5. 坐标变换

通过一系列坐标变换，用户可以通过经典的“PI”控制环间接确定和控制不随时间变化的转矩和磁通值。该过程从测量三相电机电流开始。实际上，三个电流值的瞬时总和为零。因此，只需测量三个电流中的两个，就可以确定第三个电流，这样便无需第三个电流传感器，从而降低硬件成本。

 

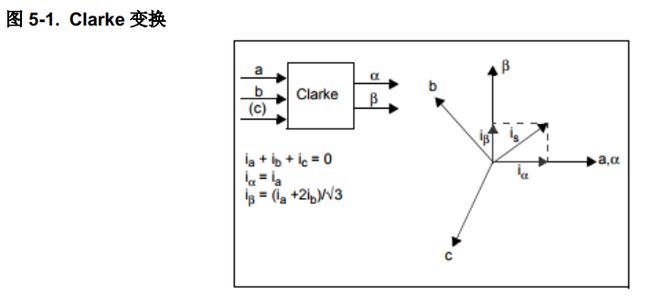
5.1 Clarke 变换

 

Clarke 变换将参考定子的三轴二维坐标系数值变换为双轴静止坐标系。图 5-1. Clarke 变换

5.2 Park 变换

 

Park 变换将双轴静止坐标系的量变换为相对于转子磁通的双轴旋转坐标系

5.3 Park

 

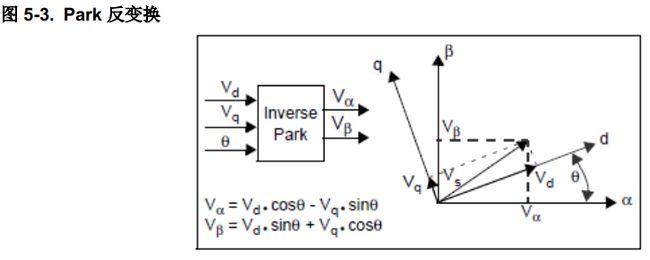
反变换Park 反变换将相对于转子磁通的双轴旋转坐标系的量变换为双轴静止坐标系

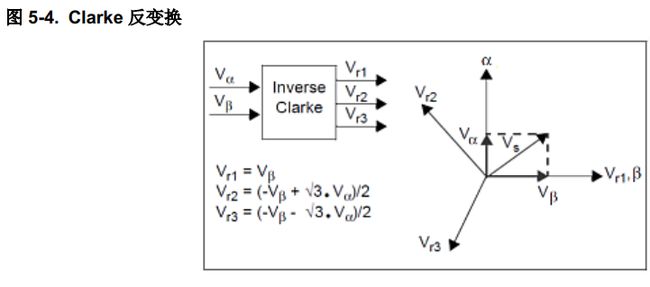
5.4 Clarke 反变换

 

Clarke 反变换将双轴静止坐标系的量变换为相对于定子的三轴二维坐标系。 alpha 和 beta 轴基于传统的Clarke 反变换实现互换，以便简化 SVPWM 实现，这将在下一节中介绍。

6. 空间矢量脉宽调制（ SVPWM）

 

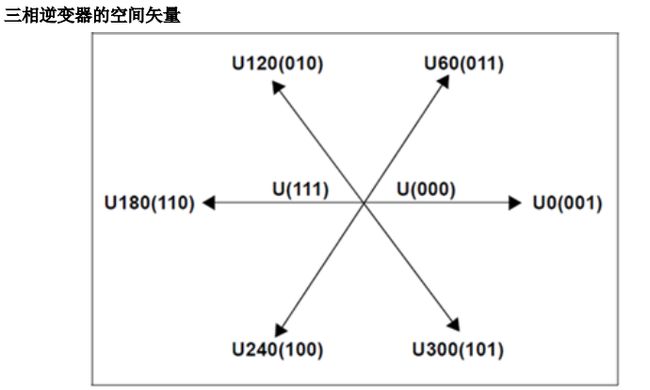
1986年，德国学者H.W.Vander Broeck等提出的基于电压空间矢量脉宽调制技术。矢量控制过程的最后一步是获取逆变器开关的脉宽调制信号来生成三相电机电压。如果使用空间矢量调制（ SVPWM）技术，则生成 PWM 的过程简化为几个简单的公式。在此实现中， Clarke 反变换集成到 SVM程序中，这进一步简化了计算过程。三个逆变器输出中的每一个均可处于两种状态之一。逆变器输出可以连接到正（ +）母线轨或负（ -）母线轨，共支持 23 = 8 种输出状态。全部三个输出都连接到正（ +）母线或负（ -）母线的两种状态被视为空状态，因为相位间无任何线电压。这两个状态绘制在 SVM 星形的原点上。其余六个状态表示为相邻状态之间有 60 度相位差的矢量，如下图所示。

SVPWM 的过程允许通过两个相邻矢量的分量之和来表示合成矢量。例如，在下图中， UOUT 为预期合成矢量。它位于 U60 和 U0 之间的区域。如果在给定 PWM 周期“T”期间， U0 施加时间 T1 并且 U60 输出时间 T2，则周期 T 产生的电压将为 UOUT。

T0 表示没有为绕组施加有效电压的时间，即，施加零矢量的时间。可使用修改后的 Clark 反变换，在不进行额外计算的情况下得出 T1 和 T2 的值。如果 Vα 和 Vβ 反转，将生成 SVM 的参考轴，此参考轴与 SVM星形偏移 30 度，如下图所示。沿约束该区域的两个轴的电压矢量时序等于 T1 和 T2。在切换周期 T 的剩余时间 T0 内施加零矢量。下图给出了对称脉冲模式的结构，这种结构产生的输出谐波最小。

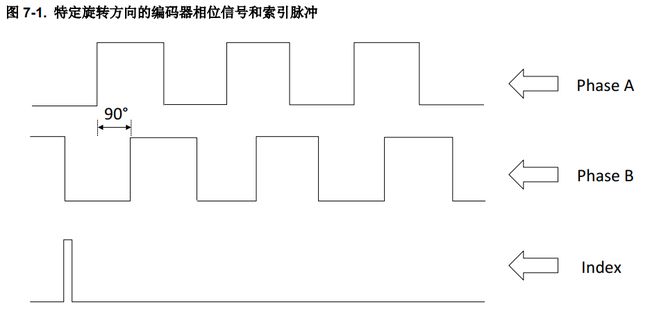
7. 位置测量

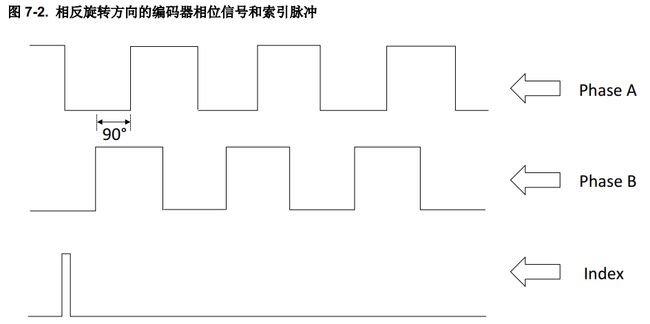
明确确切转子位置对于 FOC 正常工作至关重要。增量式光学编码器提供两个彼此正交的脉冲串，如下图所示。一些编码器具有索引脉冲，这有助于在空间上明确确切的转子位置。如果脉冲串 A 超前脉冲串 B，则电机将沿一个方向旋转，如果脉冲串 B 超前脉冲串 A，则电机将沿相反方向旋转。编码器脉冲数越多，位置测量精度就越高。

 

OK,本期实验完成！本节内容到此结束，也欢迎大家留言！！最后喜欢这个公众号的同学们记得加关注了，每天都会有技术干货推出！！

 

 

文中源码及资料下载，关注十三公众号:

在公众号里给十三发送 “下载|STM32 电机教程16” ：