Coursera | Andrew Ng (02-week3-3.6)—Batch Norm 为什么奏效？

该系列仅在原课程基础上部分知识点添加个人学习笔记，或相关推导补充等。如有错误，还请批评指教。在学习了 Andrew Ng 课程的基础上，为了更方便的查阅复习，将其整理成文字。因本人一直在学习英语，所以该系列以英文为主，同时也建议读者以英文为主，中文辅助，以便后期进阶时，为学习相关领域的学术论文做铺垫。- ZJ

Coursera 课程 |deeplearning.ai |网易云课堂

---

转载请注明作者和出处：ZJ 微信公众号-「SelfImprovementLab」

知乎：https://zhuanlan.zhihu.com/c_147249273

CSDN：http://blog.csdn.net/junjun_zhao/article/details/79122690

---

3.6 Why does batch Norm work? (Batch Norm 为什么奏效？)

(字幕来源：网易云课堂)

So, why does batch norm work?Here’s one reason, you’ve seen how normalizing the input features,the x’s,to mean zero and variance one,how that can speed up learning.So rather than having some features that range from zero to one,and some from one to a 1,000 by normalizing all the features, input features x to take on a similar range of values that can speed up learning.So, one intuition behind why batch norm works is this is doing a similar thing,but for the values in your hidden units and not just for your input there.Now, this is just a partial picture for what batch norm is doing.There are a couple of further intuitions,that will help you gain a deeper understanding of what batch norm is doing.Let’s take a look at those in this video.

为什么 batch 归一化会起作用呢？ 一个原因是 你已经看到如何归一化输入特征值 x，使其均值为 0 方差为 1，它又是怎样加速学习的，与其有一些从 0 到 1，从 1 到 1000 的特征值，通过归一化所有的输入特征值 x，以获得类似范围的值可加速学习，所以 batch 归一化起作用的原因直观的一点是，它在做类似的工作，但不仅仅对于这里的输入值 还有隐藏单元的值，这只是 batch 归一化作用的冰山一角，还有些更深层的原理，它会有助于你对 batch 归一化的作用有更深的理解，让我们一起来看看吧。

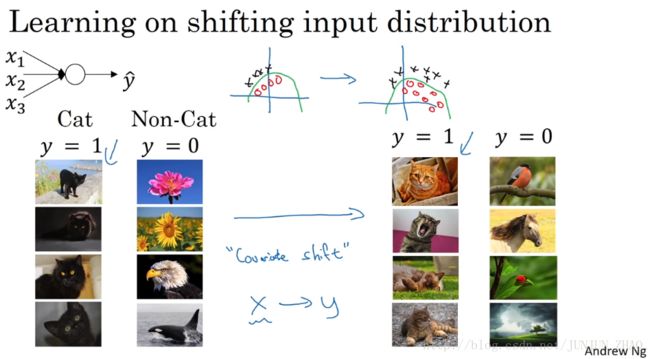
A second reason why batch norm works,is it makes weights,later or deeper than your network,say the weight on layer 10, more robust to changes to weights in earlier layers of the neural network, say, in layer one.To explain what I mean,let’s look at this most vivid example.Let’s see a training on network,maybe a shallow network,like logistic regression or maybe a neural network,maybe a shallow network like this regression or maybe a deep network,on our famous cat detection toss.But let’s say that you’ve trained your data sets on all images of black cats.If you now try to apply this network to data with colored cats where the positive examples are not just black cats like on the left,but to color cats like on the right,then your cosfa might not do very well.

Batch 归一化有效的第二个原因是，它可以使权重比你的网络更滞后或更深层，比如 第 10 层的权重更能经受得住变化，相比于神经网络中前层的权重 比如层一，为了解释我的意思，让我们来看看这个最生动形象的例子，这是一个网络的训练，也许是个浅层网络，比如 logistic 回归或是一个神经网络，也许是个浅层网络 像这个回归函数 或一个深层网络，建立在我们著名的猫脸识别检测上，但假设你已经在所有黑猫的图像上训练了数据集，如果现在你要把此网络应用于有色猫，这种情况下 正面的例子不只是左边的黑猫，还有右边其它颜色的猫，那么你的 cosfa 可能适用的不会很好。

So in pictures, if your training set looks like this,where you have positive examples here and negative examples here,but you were to try to generalize it to a data set where maybe positive examples are here and the negative examples are here,then you might not expect a module trained on the data on the left to do very well on the data on the right.Even though there might be the same function that actually works well,but you wouldn’t expect your learning algorithm to discover that green decision boundary,just looking at the data on the left.So, this idea of your data distribution changing goes by the somewhat fancy name, covariate shift.And the idea is that,if you’ve learned some x to y mapping,if the distribution of x changes,then you might need to retrain your learning algorithm.And this is true even if the function,the ground true function,mapping from x to y,remains unchanged,which it is in this example,because the ground true function is,is this picture a cat or not.And the need to retrain your function becomes even more acuteor it becomes even worse if the ground true function shifts as well.So, how does this problem of covariate shift apply to a neural network?

如果 图像中 你的训练集是这个样子的，你的正面例子在这儿 反面例子在那儿，但你试图把它们都统一于一个数据集，也许正面例子在这儿 反面例子在那儿，你也许无法期待 在左边训练得很好的模块，同样在右边也运行得很好，即使存在运行都很好的同一个函数，但你不会希望你的学习算法去发现，绿色的决策边界 如果只看左边数据的话，所以 使你数据改变分布的这个想法，有个有点怪的名字 covariate shift，想法是这样的，如果你已经学习了 x 到 y 的映射，如果 x的分布改变了，那么你可能需要重新训练你的学习算法，这种做法同样适用于，如果真实函数，由 x 到 y 映射 保持不变，正如此例中，因为真实函数，是此图片是否是一只猫，训练你的函数的需要变得更加迫切，如果真实函数也改变 情况就更糟了，covariate shift的问题怎么应用于神经网络呢？

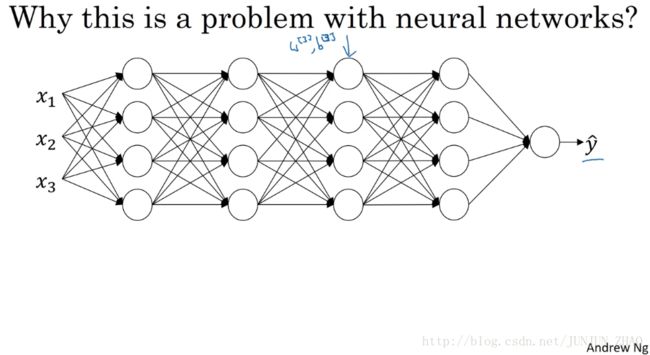
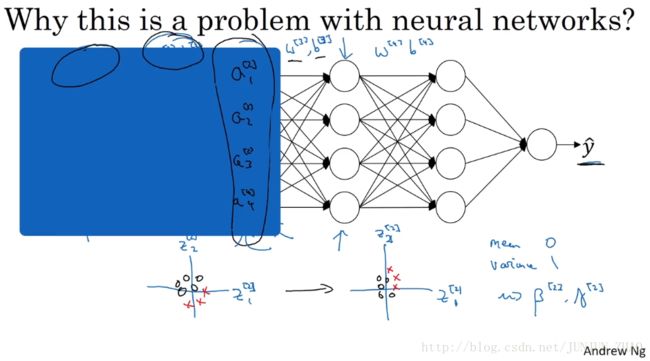
Consider a deep network like this,and let’s look at the learning processfrom the perspective of this certain layer, the third hidden layer.So this network has learned the parameters w[3] w [ 3 ] and b[3] b [ 3 ] .And from the perspective of the third hidden layer,it gets some set of values from the earlier layers,and then it has to do some stuff to hopefully make the output y-hat close to the ground true value y.So let me cover up the nose on the left for a second.So from the perspective of this third hidden layer,it gets some values,let’s call them a[2]1,a[2]2,a[2]3 a 1 [ 2 ] , a 2 [ 2 ] , a 3 [ 2 ] , and a[2]4 a 4 [ 2 ] .But these values might as well be features x[1],x[2],x[3],x[4] x [ 1 ] , x [ 2 ] , x [ 3 ] , x [ 4 ] ,and the job of the third hidden layer is totake these values and find a way to map them to y-hat.So you can imagine doing great intercepts,so that these parameters w[3] w [ 3 ] b[3] b [ 3 ] as well as maybe w[4]b[4] w [ 4 ] b [ 4 ] ,and even w[5]b[5] w [ 5 ] b [ 5 ] ,maybe try and learn those parameters,so the network does a good job,mapping from the values I drew in black on the left to the output values y-hat.mapping from the values I drew in black on the left to the output values y-hat.

试想一个像这样的深度网络，让我们从这层，第三隐藏层来看看学习过程，此网络已经学了参数 w[3] w [ 3 ] b[3] b [ 3 ] ，从第三隐藏层的角度来看，它从前层中取得一些值，接着它需要做些什么，希望使输出值 y^ y ^ 接近真实值 y y ，让我先遮住左边的东西，从第三隐藏层的角度来看，它得到一些值，称为 a[2]1a[2]2a[2]3a[2]4， a 1 [ 2 ] a 2 [ 2 ] a 3 [ 2 ] a 4 [ 2 ] ， 但这些值也可以是特征值 x[1]x[2]x[3]x[4] x [ 1 ] x [ 2 ] x [ 3 ] x [ 4 ] ，第三隐藏层的工作是，找到一种方式 使这些值映射到 y^ y ^ ，你可以想象做一些截断，所以 这些参数 w[3] w [ 3 ] b[3] b [ 3 ] ，或 w[4]b[4]w[5]b[5] w [ 4 ] b [ 4 ] w [ 5 ] b [ 5 ] ，也许是这学习这些参数，所以网络做的不错，从左边我用黑笔写的，映射到输出值 y^ y ^ 从左边我用黑笔写的，映射到输出值 y^ y ^ 。

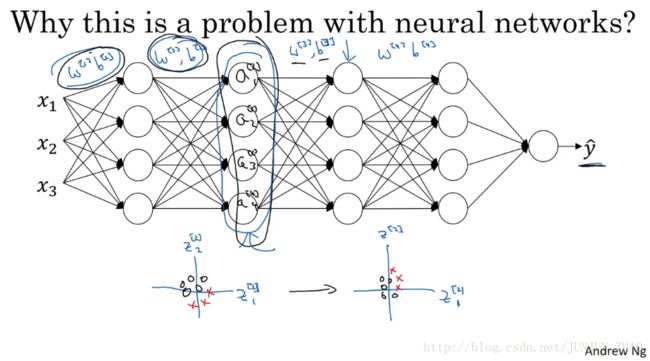
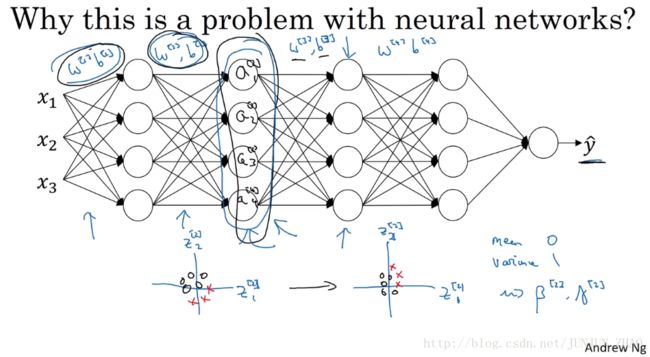
But now let’s uncover the left of the network again.The network is also adapting parameters w[2]b[2] w [ 2 ] b [ 2 ] and w[1]b[1] w [ 1 ] b [ 1 ] ,and so as these parameters change,these values, a[2] a [ 2 ] , will also change.So from the perspective of the third hidden layer,these hidden unit values are changing all the time,and so it’s suffering from the problem of covariate shift that we talked about on the previous slide.So what batch norm does,is it reducesthe amount that the distribution of these hidden unit values shifts around.And if it were to plot the distribution of these hidden unit values,maybe this is technically renormalizer z,so this is actually z[2]1 z 1 [ 2 ] and z[2]2 z 2 [ 2 ] ,and I also plot two values instead of four values,so we can visualize in 2D.What batch norm is saying is that,the values for z[2]1 z 1 [ 2 ] and z[2]2 z 2 [ 2 ] can change,and indeed they will change when the neural network updates the parameters in the earlier layers.But what batch norm ensures is that no matter how it changes,the mean and variance of z[2]1 z 1 [ 2 ] and z[2]2 z 2 [ 2 ] will remain the same.So even if the exact values of z[2]1 z 1 [ 2 ] and z[2]2 z 2 [ 2 ] change,their mean and variance will at least stay same mean zero and variance one.Or, not necessarily mean zero and variance one,but whatever value is governed by β[2] β [ 2 ] and γ[2] γ [ 2 ] .Which, if the neural networks chooses,can force it to be mean zero and variance one.Or, really, any other mean and variance.But what this does is,it limits the amount to which updating the parameters in the earlier layerscan affect the distribution of valuesthat the third layer now sees and therefore has to learn on.And so, batch norm reduces the problem of the input values changing,it really causes these values to become more stable,so that the later layers of the neural network has more firm ground to stand on.And even though the input distribution changes a bit,it changes less, and what this does is,even as the earlier layers keep learning,the amounts that this forces the later layers to adapt to as early as layer changes is reduced or,if you will, it weakens the coupling between what the early layers parameters has to do and what the later layers parameters have to do.And so it allows each layer of the network to learn by itself,a little bit more independently of other layers,and this has the effect of speeding up learning in the whole network.

现在我们把网络的左边揭开，这个网络还有参数 w[2],b[2] w [ 2 ] , b [ 2 ] 和 w[1],b[1] w [ 1 ] , b [ 1 ] ，如果这些参数改变，这些 a[2] a [ 2 ] 的值也会改变，从第三隐藏层的角度来看，这些隐藏单元的值在不断地改变，所以它就有了covariate shift 的问题，上张幻灯片中我们讲过的， batch 归一化做的，是它减少了，这些隐藏值分布变化的数量，如果是绘制这些隐藏的单元值的分布，也许这是重整值 z z ，这其实是 z[2]1 z 1 [ 2 ] z[2]2 z 2 [ 2 ] ，我要绘制两个值而不是四个值，以便我们设想为2D， batch 归一化讲的是， z[2]1 z 1 [ 2 ] z[2]2 z 2 [ 2 ] 的值可以改变，他们的确会改变，当神经网络更新参数 在之前层中， batch 归一化可确保 无论其怎样变化， z[2]1 z 1 [ 2 ] z[2]2 z 2 [ 2 ] 的均值和方差保持不变，所以即使 z[2]1 z 1 [ 2 ] z[2]2 z 2 [ 2 ] 的值改变，至少他们的均值和方差也会是均值 0 方差 1，或者不一定必须是均值 0 方差 1，而是由 β[2] β [ 2 ] 和 β[2] β [ 2 ] 决定的值，如果神经网络选择的话，可强制其为均值 0 方差 1，或 其他任何均值和方差，但它做的是，它限制了在前层的参数更新，会影响数值分布的程度，第三层看到的这种情况 因此得学习， batch 归一化减少了输入值改变的问题，它的确是这些值变得更稳定，神经网络的之后层就会有更坚实的基础，即使输入分布改变了一些，它会改变得更少 它做的是，当前层保持学习，当层改变时迫使后层，适应的程度减小了，你可以这样想,它减弱了前层参数的作用与后层参数的作用之间的联系，它使得网络每层都可以自己学习，稍稍独立于其它层，这有助于加速整个网络的学习。

So I hope this gives some better intuition,but the takeaway is that batch norm means that,especially from the perspective of one of the later layers of the neural network,the earlier layers don’t get to shift around as much,because they’re constrained to have the same mean and variance.And so this makes the job of learning on the later layers easier.It turns out batch norm has a second effect,it has a slight regularization effect.So one non-intuitive thing of a batch norm is that each mini- batch ,I will say mini- batch x[t] x [ t ] ,has the values z[t] z [ t ] ,has the values z[l] z [ l ] ,scaled by the mean and variance computed on just that one mini- batch .Now, because the mean and variance computed on just that mini- batch as opposed to computed on the entire data set,that mean and variance has a little bit of noise in it,because it’s computed just on your mini- batch of,say, 64, or 128,or maybe 256 or larger training examples.So because the mean and variance is a little bit noisy because it’s estimated with just a relatively small sample of data,the scaling process,going from z[1] z [ 1 ] to Z̃ [l] Z ̃ [ l ] ,that process is a little bit noisy as well,because it’s computed, using a slightly noisy mean and variance.So similar to dropout ,it adds some noise to each hidden layer’s activations.The way dropout has noises,it takes a hidden unit and it multiplies it by zero with some probability.And multiplies it by one with some probability.And so your dropout has multiple of noise because it’s multiplied by zero or one,whereas batch norm has multiples of noise because of scaling by the standard deviation,whereas batch norm has multiples of noise because of scaling by the standard deviation,as well as additive noise because it’s subtracting the mean.Well, here the estimates of the mean and the standard deviation are noisy.And so, similar to dropout , batch norm therefore has a slight regularization effect.Because by adding noise to the hidden units,it’s forcing the down stream hidden units not to rely too much on any one hidden unit.

所以 希望这能带给你更好的直觉，重点是 batch 归一化的意思是，尤其从神经网络后层之一的角度而言，前层不会左右移动的那么多，因为它们被同样的均值和方差所限制，所以 这会使得后层的学习工作变得更容易些， batch 归一化还有一个作用，它有轻微的正则化效果， batch 归一化中非直观的一件事是每个 mini- batch ，我会说 mini- batch x[t] x [ t ] ，的值为 z[t]z[l] z [ t ] z [ l ] ，在 mini- batch 计算的 由均值和方差缩放的，因为在 mini- batch 上计算的均值和方差，而不是在整个数据集上，均值和方差有一些小噪音，因为它只在你的 mini- batch 上计算，比如 64 或 128 或 256，或更大的训练例子，因为均值和方差有一点小噪音，因为它只是由一小部分数据估计得出的，缩放过程从 z[1] z [ 1 ] 到 Z̃ [l] Z ̃ [ l ] ，过程也有一些噪音，因为它是用有些噪音的均值和方差计算得出的，所以和 dropout 相似，它往每个隐藏层的激活值上增加了噪音， dropout 有噪音的方式，它使一个隐藏的单元 以一定的概率乘以 0，以一定的概率乘以 1，所以你的 dropout 含几重噪音，因为它乘以 0 或 1，对比而言 batch 归一化含几重噪音，因为标准偏差的缩放，对比而言 batch 归一化含几重噪音，因为标准偏差的缩放，和减去均值带来的额外噪音，这里均值和标准偏差的估值也是有噪音的。

And so similar to dropout ,it adds noise to the hidden layersand therefore has a very slight regularization effect.Because the noise added is quite small,this is not a huge regularization effect,and you might choose to use batch norm together with dropout ,and you might use batch norm together with dropout sif you want the more powerful regularization effect of dropout .And maybe one other slightly non-intuitive effect is that,if you use a bigger mini- batch size,right, so if you use a mini- batch size of, say,512 instead of 64,by using a larger mini- batch size,you’re reducing this noiseand therefore also reducing this regularization effect.So that’s one strange property of dropout which is that by using a bigger mini- batch size,you reduce the regularization effect.Having said this, I wouldn’t really use batch norm as a regularizer,that’s really not the intent of batch norm,but sometimes it has this extra intendedor unintended effect on your learning algorithm.But, really, don’t turn to batch norm as a regularization.Use it as a way to normalize your hidden units activations and therefore speed up learning.And I think the regularization is an almost unintended side effect.

所以类似于 dropout ， batch 归一化有轻微的正则化效果，因为给隐藏单元添加了噪音，这迫使后部单元，不过分依赖任何一个隐藏单元，类似于 dropout ，它给隐藏层增加了噪音，因此有轻微的正则化效果，因为添加的噪音很微小，所以并不是巨大的正则化效果，你可以将 batch 归一化和 dropout 一起使用，你可以将两者共同使用，如果你想得到 dropout 更强大的正则化效果，也许另一个轻微的非直观的效果是，如果你应用了较大的 mini- batch ，对 比如说 你用了，512 而不是 64，通过应用较大的 mini- batch ，你减少了噪音，因此减少了正则化效果，这是 dropout 的一个奇怪的性质，就是应用较大的 mini- batch ，可以减少正则化效果，说到这儿 我把会把 batch 归一化当成一个规则，这确实不是其目的，但有时他会对你的算法有额外的期望效应，或非期望效应，但是不要把 batch 归一化当作规则，把它当作将你归一化隐藏单元激活值，并加速学习的方式，我认为正规化几乎是一个意想不到的副作用。

So I hope that gives you better intuition about what batch norm is doing.Before we wrap up the discussion on batch norm,there’s one more detail I want to make sure you know,which is that batch norm handles data one mini- batch at a time.It computes mean and variances on mini- batch es.So at test time,you try and make predictors, try and evaluate the neural network,you might not have a mini- batch of examples,you might be processing one single example at the time.So, at test time you need to do something slightly differently to make sure your predictions make sense.Like in the next and final video on batch norm,let’s talk over the details of what you need to do in order totake your neural network trained using batch norm to make predictions.

所以希望这能让你更理解 batch 归一化的工作，在我们结束 batch 归一化的讨论之前，我想确保你还知道一个细节， batch 归一化一次只能处理一个 mini- batch 数据，它在 mini- batch 上计算均值和方差，所以测试时，你试图做出预测试着评估神经网络，你也许没有 mini- batch 例子，你也许一次只能进行一个简单的例子，所以测试时 你需要做一些不同的东西，以确保你的预测有意义，在下一个和最后的 batch 归一化的视频中，让我们详细谈谈你需要的细节，来让你的神经网络应用 batch 归一化来做出预测。

---

重点总结：

Batch Norm 起作用的原因

First Reason

首先 Batch Norm 可以加速神经网络训练的原因和输入层的输入特征进行归一化，从而改变 Cost function 的形状，使得每一次梯度下降都可以更快的接近函数的最小值点，从而加速模型训练过程的原理是有相同的道理。

只是 Batch Norm 不是单纯的将输入的特征进行归一化，而是将各个隐藏层的激活函数的激活值进行的归一化，并调整到另外的分布。

Second Reason

Batch Norm 可以加速神经网络训练的另外一个原因是它可以使权重比网络更滞后或者更深层。

下面是一个判别是否是猫的分类问题，假设第一训练样本的集合中的猫均是黑猫，而第二个训练样本集合中的猫是各种颜色的猫。如果我们将第二个训练样本直接输入到用第一个训练样本集合训练出的模型进行分类判别，那么我们在很大程度上是无法保证能够得到很好的判别结果。

这是因为第一个训练集合中均是黑猫，而第二个训练集合中各色猫均有，虽然都是猫，但是很大程度上样本的分布情况是不同的，所以我们无法保证模型可以仅仅通过黑色猫的样本就可以完美的找到完整的决策边界。第二个样本集合相当于第一个样本的分布的改变，称为：Covariate shift。如下图所示：

那么存在Covariate shift的问题如何应用在神经网络中？ 就是利用Batch Norm来实现。如下面的网络结构：

网络的目的是通过不断的训练，最后输出一个更加接近于真实值的 y^ y ^ 。现在以第 2 个隐藏层为输入来看：

对于后面的神经网络，是以第二层隐层的输出值 a[2] a [ 2 ] 作为输入特征的，通过前向传播得到最终的 y^ y ^ ，但是因为我们的网络还有前面两层，由于训练过程，参数 w[1] w [ 1 ] ， w[2] w [ 2 ] 是不断变化的，那么也就是说对于后面的网络， a[2] a [ 2 ] 的值也是处于不断变化之中，所以就有了 Covariate shift 的问题。

那么如果对 z[2] z [ 2 ] 使用了 Batch Norm，那么即使其值不断的变化，但是其均值和方差却会保持。那么 Batch Norm 的作用便是其限制了前层的参数更新导致对后面网络数值分布程度的影响，使得输入后层的数值变得更加稳定。另一个角度就是可以看作，Batch Norm 削弱了前层参数与后层参数之间的联系，使得网络的每层都可以自己进行学习，相对其他层有一定的独立性，这会有助于加速整个网络的学习。

Batch Norm 正则化效果

Batch Norm还有轻微的正则化效果。

这是因为在使用 Mini-batch 梯度下降的时候，每次计算均值和偏差都是在一个 Mini-batch 上进行计算，而不是在整个数据样集上。这样就在均值和偏差上带来一些比较小的噪声。那么用均值和偏差计算得到的 z˜[l] z ~ [ l ] 也将会加入一定的噪声。

所以和 Dropout 相似，其在每个隐藏层的激活值上加入了一些噪声，（这里因为 Dropout 以一定的概率给神经元乘上 0 或者 1）。所以和 Dropout 相似，Batch Norm 也有轻微的正则化效果。

这里引入一个小的细节就是，如果使用 Batch Norm ，那么使用大的 Mini-batch 如 256，相比使用小的 Mini-batch 如 64，会引入跟少的噪声，那么就会减少正则化的效果。

参考文献：

[1]. 大树先生.吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记（2-3）– 超参数调试和 batch Norm

---

PS: 欢迎扫码关注公众号：「SelfImprovementLab」！专注「深度学习」，「机器学习」，「人工智能」。以及 「早起」，「阅读」，「运动」，「英语 」「其他」不定期建群 打卡互助活动。