s调irs

• 最佳的最大似然检测器和低复杂度的压缩传感检测器。

一、调制方案

所有方案均为单输出多输入（SIMO）。一个发射机TA，两个IRS，$N_R$个接收机RA。每个IRS有一个或多个反射面RS，每个反射面（RS）有多个原件。

三种方案的流程：

• （1）IRS1选择性的激活IRS2中的某个元件
  1）输入的比特序列分为两部分。第一部分选择用传统的PSK/QAM符号，第二部分利用波束索引调制。
  2）TA与IRS1保持靠近。他们彼此进行优先和无线的链接。序列第一部分PSK/QAM的选择由发射机进行选择，并通过无线的方式发送到IRS1的RS。
  3）有线连接用于将序列第二部分映射为波束索引调制。这部分通过适当改变相位，将信号发送到IRS1的RS上。
  4）基于接受的相位向量，IRS1的元件可将入射信号调整为所需的相移，之后发送到IRS2。相位是特殊调整的，以确保仅有期望的IRS2的元件接受到信号。这种特殊选择为索引调制保留了信息位。
  5）IRS2反射信号（有或没有相移根据方案的选择）。并由RA接受信号。RA的信息检测包含传统的PSK/QAM符号及IRS2的特定元素索引反射的符号。这是由$N_R$个RA共同完成的。

对于细节有如下假设：

1）发射机到IRS1的距离非常小。因此信道为噪声可忽略的高斯信道。
2）IRS1和IRS2直接仅有LOS路径。这种假设是合理的，因为两个反射面共在一个封闭空间，IRS1的元件通过调整相位，特殊的选择IRS2的元件进行接受。因此，假设IRS1和IRS2也假设为高斯信道。
3）在IRS2和接收端之间假设为平坦衰落的瑞利信道。信道系数根据$\mathcal{C}\mathcal{N}(0,1)$。

A方案1：单符号索引调制

在这个方案中，两个IRS均有单个RS。IRS1与IRS2相距为D。IRS1有$(N_{1H}\times N_{1W})$个元件，IRS2有$(N_{2H}\times N_{2W})$个元件。$N_{1}and{N}_2$为IRS1和IRS2元件的总数量。TA发送符号到IRS1，每个元件在入射波上应用特殊的相移，使IRS2只有一个元件接受到信号。因此这种方案的比特位数为$lo{g}_{2}M+\lfloor lo{g}_2{N}_2\rfloor$。最后IRS2反射信号，并通过RAs进行接收。
$s$为发射信号。IRS1接收的符号为$s+w_1$，这里$w_1\sim \mathcal{C}\mathcal{N}(0,{\sigma }_1^2)$。然而在假设1中，${\sigma }_1^2\approx 0$并且$w_1$可以忽略。因此，IRS2的接收向量为
$${\mathbf{x}}_2=\mathbf{b}s+{\mathbf{w}}_2$$
这里$w_2\sim \mathcal{C}\mathcal{N}(0,{\sigma }_2^2)$，$\mathbf{b}$是$N_2\times 1$的向量。在理想条件下，$\mathbf{b}$应该只有一个与光束索引相对应的非零项（等效于IRS2中的选定元素）。但是，这实际上将不会发生，因为有限功率也会分散在其他方向上，并且此功率分布取决于IRS1每个元素的相对权重。RA处的向量可写为：
$$\begin{gathered} \mathbf{y}=\mathbf{H}{\mathbf{x}}_2+{\mathbf{w}}_R \\ =\mathbf{H}\mathbf{b}s+\mathbf{w} \end{gathered}$$
这里$\mathbf{H}$表示在假设3和${\mathbf{w}}_R\sim \mathcal{C}\mathcal{N}(0,{\sigma }_R^2)$下$N_R\times N_2$信道矩阵。$\mathbf{w}=\mathbf{H}{\mathbf{w}}_2+{\mathbf{w}}_R$是具有$\mathcal{C}\mathcal{N}(0,\sum )$分布的加性噪声，$\sum =\mathbf{H}{\mathbf{H}}^{\mathbf{H}}{\sigma }_2^2+{\sigma }_R^2\mathbf{I}$。最终，接收端必须从$\mathbf{y}$中检测出$\mathbf{b}$和$s$才能解码出传输的比特。

B方案2：多符号索引调制

结构如图2所示。在该方案中，IRS1有$N_T$个RS。调制器根据索引调制的$N_T$个不同相位向量，并发射到IRS2的不同RS上。因此，$N_T$个RSs将传统的PSK/QAM映射到IRS2上不同的$N_T$个元件。因此，该方案总的比特位数为$lo{g}_{2}M+\lfloor lo{g}_2(\underset{N_T}{N_2})\rfloor$。可以使用查找表方法或组合方法来组织要激活的元素的选择。该方案也可用等式（1）和（2）表示，不同的是$\mathbf{b}$有$N_T$个非零项。

C方案3：最大信噪比的单符号索引调制

如图三所示，该方案与方案1相似，区别在于每个IRS2的元件由$N_3$个元件组成的RS代替。所以IRS2的元件总数变为$N_2{N}_3$，TA和IRS1都以与方案1相同的方式运行。相比与其他两种方案，该方案的IRS2可对入射信号进行相移。该相移可使接收端信噪比最大化。
因此，接收信号可表示为：
$$\mathbf{y}=\mathbf{H}\Xi \mathbf{b}s+\mathbf{w}$$
这里$\Xi$表示$(N_2{N}_3\times N_2{N}_3)$的IRS2相移对角矩阵。在上式中$\mathbf{H}$是$(N_R\times N_2{N}_3)$的矩阵。信噪比可表示为：
$$\text{SNR}=\frac{\Vert \mathbf{H}\Xi \mathbf{b}s{\Vert }^2}{\text{Var}(\Vert \mathbf{w}\Vert )}$$
令${\xi }_{1:N_2{N}_3}$表示$\Xi$的对角线的项。因此，SNR最大可表示为：
$$\begin{gathered} \underset{{\xi }_l}{\max }\Vert \mathbf{H}\Xi \mathbf{b}s{\Vert }^2 \\ s.t.|{\xi }_l|=1,\forall l=1,2,...,N_2{N}_3. \end{gathered}$$
以上优化问题具有如下挑战：
IRS2是无源设备，解决复杂的优化问题是不且实际的。理想地优化应该在发射机或接收机处进行，并且所得到的信息必须传达给IRS2。如果优化取决于要传输的数据（bs），则必须在每个时隙中进行更新，这是相当大的通信开销。因此，优化应该优选地仅取决于bs的平均值，或者实际上理想地应该独立于它。因此，我们将针对（5）提出以下解决方案。
1）方法1：这种方法基于存在理想波束形状的假设。在IRS2中选定的所有RS接收到相同的功率，同时所有的其他元件接收到的功率为0。不失一般性的（Without loss of generality），将该常数设置为1。优化函数（5）可重写为：

这里$1$表示1s，$\xi$是由$\Xi$的对角元素形成的向量。因此，最大化问题变为：

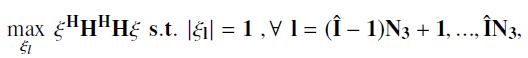
这里$\hat{I}$表示IRS2的RS的特定选择。令${\xi }_l=e^{j{\alpha }_l}$,$|{\xi }_l|=1$。记住这一点（Bearing this in mind），并且${\mathbf{H}}^H\mathbf{H}$是埃尔米特矩阵。公式（5）可重写为以下无约束形式：

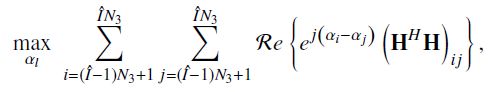
这里$({\mathbf{H}}^H\mathbf{H}{)}_{ij}$表示${\mathbf{H}}^H\mathbf{H}$的第$(i,j)$个元素。因为上式是非凸函数，只能通过一些交替技术来找到该函数的局部最大值。
2）方法2：该方法依赖于假设$N_R\ge N_3$。RAs的数量要大于IRS2的RS个数。

引理1：令${\mathbf{H}}_{Q}and{\Xi }_Q$分别作为$\mathbf{H}and\Xi$对应于所选RS的子矩阵$(N_R\times N_3)and(N_3\times N_3)$，令${\mathbf{b}}_Q$对应于$\mathbf{b}$的子向量。如果$N_R\ge N_3$的概率为1，边界：

是非凡的，等同于

附录A：

${\Xi }_Q^H{\mathbf{H}}_Q^H{\mathbf{H}}_Q{\Xi }_Q\text{and}({\mathbf{b}}_{Q}s)({\mathbf{b}}_{Q}s{)}^H$是正定矩。因此，上式应用【文献58】可得到（9）式。因为${\mathbf{H}}_Q$是一个随机矩阵，且如果$R\ge Q$(接收天线数大于IRS2有效反射元件数)，${\mathbf{H}}_Q^H{\mathbf{H}}_Q$是一个满秩矩阵的概率为1，因此最小特征值${\lambda }_{min}({\Xi }_Q^H{\mathbf{H}}_Q^H{\mathbf{H}}_Q{\Xi }_Q)>0$。

引理1可用来解决优化问题（5）。思想是最大化非凡下限，而不是实际函数。因此，优化问题（5）变成：

这里式（11）是一个约束非线性极小极大优化问题。这可直接解决【有文献】。它可通过引入额外的变量来转换成一个非线性最大化问题，然后使用标准技术来求解。

需要注意的是，这两种SNR最大化问题的方案，$\hat{I}$是IRS2中所选择的RS的数据，它必须优化的，且取决于信息位。为了避免优化对信息位的依赖性，每个RS要分别优化，无论信道有多大的变化。优化相位信息传送给IRS2，并将其应用到所有元件，而不是所选择的RS。多符号方案同样适用。最终，IRS2上所有被激活的RS将通过相移来提升SNR。因此，这两个方案将会提高信息速率和SNR。实际上，最佳相移一定要在接收端来评估，并传送到IRS2。

索引调制的实现

索引调制的背后原理是IRS2特定元件的激活。为了计算相移，假设IRS1和IRS2之间仅有LOS路径。因此，相移仅由IRS对决定。
设IRS1的中心作为原点坐标（0，0，0），$\mathbf{P}$是IRS1元件的位置向量。根据输入比特序列，由IRS1来激活IRS2的第n个元件。$({\theta }_n^h,{\theta }_n^v)$表示关于原点的方位角和仰角对。由IRS1的元素给定以选择第n个波束的相位矢量为$\varphi =2\pi f\tau$，这里$\tau =\frac{{\mathbf{P}}^H{\mathbf{u}}_n}{c}$,$c$为光速，$f$为载频频率。

在多比特波束索引调制的情况下，必须根据输入比特序列为每个IRS计算这些相移。
另外，如果IRS元件调整输入信号的幅度和相位，可以修改每个元素的相对权重。因为IRS由无源设备构成，放大难以实现，然而减小很容易应用到入射信号。减小的调整可以通过一个窗函数对波束成形和波束图案进行修改。这将有利于减小干扰。

A参数设计

参数涉及IRS1和IRS2的元件数及它们之间的距离。令$\lambda$表示对应最高工作频率的波长。设计的固定参数如下：
1）IRS1中内部元件的间距（$d_1$）：IRS1中的每个RS元件的间距为$\frac{\lambda }{2}$。例如，最大工作频率$f_{max}=60GHz$，那么$d_1=2.5mm$。现在，如果IRS1有$100\times 100$个元件，那么它的尺寸将为$0.25\times 0.25m$。该间距对于避免使用IRS1形成的波束中的光栅波瓣很重要。
2）两个IRS之间的距离（D）：距离D应该满足远场条件$D>\frac{2L^2}{\lambda }$，L为RS的长度。在上面的例子中，D>25m。如果满足该条件，，那么就假设从IRS1到IRS2的波是平面的。
3）IRS2内部元件的间距（$d_2$）：IRS2中每个元件的宽度$(d_w)$应该小于$D{\theta }_{BW}$，这里${\theta }_{BW}$是IRS1的波束宽度，同时IRS2元件之间的宽度$d_2$应大于该值。这就确保了预期元件或者仅有预期元件接收到来自IRS1的反射信号。对于一个矩形窗，波束宽度近似为${\theta }_{BW}\approx \frac{50\lambda }{L}$。在该例子中，${\theta }_{BW}\approx 1^0$，对应最小频率。因此，当$D=25m$时，$d_w<48cm\text{and}{d}_2>48cm$。现在，如果$N_{1H}=N_{1W}=8$,IRS2的近似尺寸为$4m\times 4m$。
4）IRS1的元件数$(N_1)$：IRS1的元件数决定了阵列的长度L和波束宽度${\theta }_{BW}$。这些参数决定两个IRS的距离和IRS2内元件的间距。
5）IRS2的元件数$(N_2)$：这决定系统的传输速率。很大的$N_2$将提供高传输速率。然而这将使IRS2的尺寸变大。因此，$N_2$受最大陈列尺寸的限制。

三、检测器

检测器必须恢复出QAM/PSK符号和IRS2的元件激活模式。也就是必须要检测出(2)或(3)式$\mathbf{y}$中的s和$\mathbf{b}$。令$\mathbf{x}=\mathbf{b}s$，（2）和（3）式可写为：
$$\mathbf{y}=\mathbf{A}\mathbf{x}+\mathbf{w}(12)$$
这里在方案1和2中$\mathbf{A}=\mathbf{H}$。在方案3中$\mathbf{A}=\mathbf{H}\Xi$。假设$\mathbf{A}$在接收端是已知的。

A、最佳检测器

1）单符号方案：考虑式（12）中的向量$\mathbf{x}$。理想中单符号方案的$\mathbf{x}$内仅有一项非零值，因为只有一个元件接收到信号。但这是不可实现的，因为波束成形也会使其他方向非零。现实中在IRS2上有超过一个元件接收到信号。然而，不期望的波束索引的功率远低于期望的索引功率，并且这些功率取决于IRS1使用的窗函数功能。
在上一节的A中，IRS2的元件间距$d_2=1.0m$,这大概等于所需最小距离的两倍。对于这个问题，图四显示了$\mathbf{x}$的各个索引对应的功率，此时期望的索引是28。

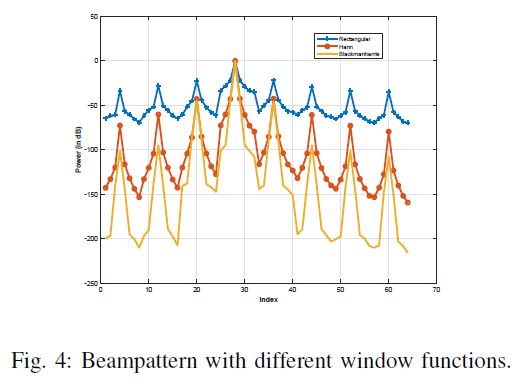
三种窗类型的功率模式，分别为rectangular, Hann and Blackman Harris。考虑所有功率小于40dB的系数为零。因此，rectangular窗有8个非零索引，另外两个仅有一个主要索引。
现在，数据依靠索引的变化，不论用的什么窗函数，图4的模式将会移到不同索引。式（12）可写为：
$$\mathbf{y}=\mathbf{A}{\Pi }_{\mathbf{p}}+\mathbf{w}$$
这里$\mathbf{p}$表示$\mathbf{x}$各种索引功率向量，${\Pi }_{\mathbf{p}}$表示功率模式的一个特定排列。因此，为了识别波束索引，必须识别功率模式排列${\Pi }_{\mathbf{p}}$。现在，$\mathbf{y}\sim \mathcal{C}\mathcal{N}(\mathbf{A}{\Pi }_{\mathbf{p}},\Sigma )$。因此，这个问题的ML检测器可写为：

一般的，搜索问题（14）是NP-hard。然而，在该例子中，仅有$N_{2}M$个不同的模式对应$N_2$个不同的波束索引，和M个QAM/PSK符号。因此，中等复杂度的搜索将为ML检测器（14）提供最佳解决方案。
2）多符号方案：ML检测器也适用于多符号情况。然而，在同一时间有$N_T$个期望的波束索引同时存在，彼此相互作用，从而产生大量${\Pi }_{\mathbf{p}}$可能的组合。明确的是，必须为IRS1中的$N_T$个RS测试$(\underset{N_T}{N_2})M$个不同模式的假设。因此，ML检测器不再是计算的好方法。

B、次优压缩感知检测器

当活动元素（即接收符号的元素）的数量远小于IRS2中元素的总数时，（12）中的传输向量$\mathbf{x}$稀疏。因此，可以使用一种高效的稀疏重建算法，来识别$\mathbf{x}$中的非零项，并用来估计$\mathbf{b}$。因此，为了成功的恢复出稀疏向量$\mathbf{x}$，需要足够的测量次数。这可通过足够的RAs数量（$N_R$足够大）和多次测量来实现，这自然会降低数据速率。最终，可从估计的$\mathbf{b}$中得到s：
$$\hat{s}=\underset{s\in \mathcal{M}}{\min }\Vert \mathbf{y}-\mathbf{b}s{\Vert }^2$$
这里$\mathcal{M}$是使用的星座。

C、复杂度

最佳ML检测器要计算式（14）中的所有可能的组合，这大约需要$(N_R^3+N_R{N}_2)$次乘法。这对每个可能的符号都要进行计算。对于多符号的情况，有$(\underset{N_T}{N_2})M$个可能的符号。因此，总的计算复杂度约为$(\underset{N_T}{N_2})M(N_R^3+N_R{N}_2)$次，对于单符号将减少到$N_{2}M(N_R^3+N_R{N}_2)$。另一方面，如果使用任何类型的基于压缩感知的次优算法，这个复杂度将会降低到$N_2{N}_R{N}_T$，这相比于最佳ML检测器低多了。

四、平均误码率

在这部分，将评估最佳ML检测器的平均误码率上界。令$Pr\{{\Pi }_{\mathbf{p}}^i\to {\Pi }_{\mathbf{p}}^j\}$表示模型${\Pi }_{\mathbf{p}}^i$被识别成${\Pi }_{\mathbf{p}}^j$的概率，$v_{i,j}$表示这两个排列的错误位数量。平局BER可写为：

这里$n_b$表示每个信道使用的总位数，$\Omega$是可能排列的总数。式（16）假设所有排列都是等可能的。式（16）中的符号错误概率$Pr\{{\Pi }_{\mathbf{p}}^i\to {\Pi }_{\mathbf{p}}^j\}$可由以下写出。当${\Pi }_{\mathbf{p}}^i$被发送时，检测器基于下式识别成${\Pi }_{\mathbf{p}}^j$作为传输符号：

这里$\mathbf{y}$和${\Pi }_{\mathbf{p}}={\Pi }_{\mathbf{p}}^i$由（13）式给出。定义：

因此，有：

式（18）中相交事件概率的计算式非常复杂的。因此，使用Fretchet’s不等式界定：

为了评估该界，对于每个$k\ne j$，概率$Pr\{r_j>r_k\}$一定要进行计算。定理1给出了这个概率的表达式：

定理1：

假设$\text{A}\sim \mathcal{C}\mathcal{N}(0,\mathbf{I})$和${\sigma }_2^2\ll {\sigma }_R^2$。当${\Pi }_{\mathbf{p}}^i$是实际传输信号时，$Pr\{r_j>r_k\}$由以下给出：

最终，对于每个传输符号${\Pi }_{\mathbf{p}}^i$，$\forall k\ne j$，概率$Pr\{r_j>r_k\}$的最小值可通过定理1进行计算，将$Pr\{{\Pi }_{\mathbf{p}}^i\to {\Pi }_{\mathbf{p}}^j\}$带入（16）式中可得到平均BER的界。
平均BER的边界导出值可用于方案1和方案2，因为在这两种方案中$\mathbf{A}=\mathbf{H}$。方案1中，$\Omega =N_{2}M,n_b=lo{g}_{2}M+\lfloor lo{g}_2{N}_2\rfloor$。方案2中，$\Omega =（\underset{N_T}{N_2}）M,n_b=lo{g}_{2}M+\lfloor lo{g}_2(\underset{N_T}{N_2})\rfloor$。方案3中，$\mathbf{A}=\mathbf{H}\Xi$，因此$\mathbf{A}$不再服从分布$\mathcal{C}\mathcal{N}(0,\mathbf{I})$。但是，附录C中得出的条件概率也可以用于方案3。基于此，可以使用采样方法来计算边界，从而得出无条件概率。

五、仿真结果

• 频段：55-60GHz
• IRS1：$100\times 100$的矩形阵列，间距2.5mm。这对应最高频60GHz的半波长。
• 两个IIRS之间的距离（D）：30m。这个距离满足IRS1的远场条件。
• IRS2：$8\times 8$的举行阵列，间距$d_2=60cm$。这些参数会针对不同性能研究进行修改。
  所有仿真采用16QAM。结果为$10^5$次蒙特卡洛实验。信道完美已知。
  
  
  图5和图6为方案一的性能。
  从图6可看出，低复杂度CS检测器不如ML检测器。图6是针对d2 = 85 cm（约为最小距离的1.5倍）绘制的，以适应“ Hann”窗的更大光束宽度。当IRS2中的元素间间距加倍时，以及使用窗口功能时，CS检测器的性能也会得到改善。
  
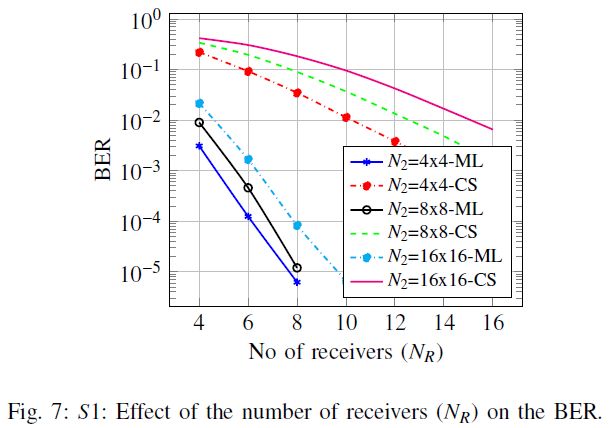
  图7所示，可以通过增加RA的数量来提高CS检测器的性能。对于相同的RA数，随着$N_2$的增加，性能有所降低，但数据速率会增加。
  
  图8中S2的$N_T=2$，三种方式的元件数量相同。在S3中，$2\times 2$代替一个元件。因此，IRS2在S3中的有效尺寸为4×4，而在S1和S2的情况下为8×8。因此，由于IRS1中有更多的RS，因此S3的数据速率最低，而S2的数据速率最高。图例S3O1和S3O2分别代表两种优化方法的结果，即（8）和（11）的解。这两种方案的性能均优于S1和S2。这是因为由于优化，接收到的SNR有所增加。
  
  图9显示了随着IRS1的RS（$N_T$）数量变化，在CS检测器下，应用方案3，不同数量的接收设备（$N_R$）的误码率变化。平均BER随着$N_T$的增加而增加，这可以通过增加接收器的数量来减小。但$N_T$的增加可使数据速率增加。在这种情况下，对于单个RS情况（相当于S1），数据速率为10 bpcu，而对于NT = 2、4、6和8，数据速率为14、23、30和36。
  图10中，说明了信道估计误差的影响。图中显示了有和没有信道估计的平均BER。通过添加方差为${\sigma }_R^2$的噪声来破坏真实的信道系数。可以看出，由于信道估计误差，S1和S2的性能均下降约2-3 dB，而S3的这一差距超过4 dB。这是因为在S3中，受污染的信道信息既用于优化又用于检测。

《Intelligent Reflecting Surface Assisted Beam Index-Modulation
for Millimeter Wave Communication》