智能反射面信道估计论文: Channel Estimation for Reconfigurable Intelligent Surface Aided Multi-User MIMO Systems

这篇博文是对arxiv文章： 《这篇博文是对magazine文章： 《Channel Estimation for Reconfigurable Intelligent Surface Aided Multi-User MIMO Systems》的读后感记录，原文可在arxiv查找到。

作者是 Jie Chen, Student Member, IEEE, Ying-Chang Liang, Fellow, IEEE, Hei Victor Cheng, Member, IEEE, and Wei Yu, Fellow, IEEE

文章简介

在上一篇博文中，magazine文章详细列举了智能反射面的多种用途。与此同时，许多基于智能反射面系统的波束成形设计已被广泛研究。 然而，这些研究往往基于完美信道信息的假设， 但实际中， 由于智能反射面本身并不能进行信号处理， 因此相比于传统通信系统，会导致对信道的估计非常艰难。 这篇文章便是提出了智能反射面系统的一种上行信道估计算法。 根据信道的稀疏性， 作者使用了压缩感知类的算法来做信道估计。

文章贡献

• 作者指出， 由于基站与反射面往往安置在相近高度，因此其间的散射非常少， 即信道径数很有限。 因此，智能反射面系统的信道有类似于毫米波信道的稀疏性。 但是，由于智能反射面的信道由两部分组成，因此他的稀疏性又有别于普通的毫米波信道， 作者称之为 row-column-block sparse。 这个后面后细说。
• 基于这一特殊的稀疏性， 作者针对性地提出了一种压缩感知算法， 可以相比传统方法更好的恢复信道。
• 由于变量之间的耦合，本文采用了一种交替迭代优化的算法（alternating optimizaiton），并且分析了其收敛性。

系统模型

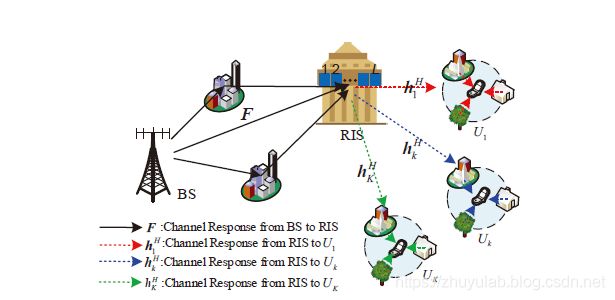
如图，文章考虑的是一个基站通过智能反射面，服务于多个用户的场景。 以下是一些符号：

• $K$: 用户数
• $M$: 基站天线数 （假定用户为单天线）
• $L$: 智能反射面反射元件数
• $U_1,...,U_k$, 用户$1$,…用户$k$
• $\mathbf{F}$: $L\times M$, 基站到反射面的信道
• ${\mathbf{h}}_k^H$: $1\times L$, 反射面到$k$用户的信道
• ${\mathbf{V}}_o=\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}({\mathbf{v}}_0)$： $L\times L$的对角阵， 表示反射面对入射信道的处理（幅度和相位的调整）。本文中认为只有相位的调整。
• 整个信道可表示为： ${\mathbf{h}}_k^H{\mathbf{V}}_o\mathbf{F}$

由于${\mathbf{h}}_k^H\mathrm{diag}(\mathbf{v})={\mathbf{v}}^T\mathrm{diag}\left({\mathbf{h}}_k^H\right)$, 我们真正要估计的信道信息其实就是：
$$G_k=\mathrm{diag}\left(h_k^H\right)F\in {\mathbb{C}}^{L\times M}$$

这一点非常重要。 但必须指出的是，这是基于用户端是单天线的假设，如果多天线的话则不再成立。

估计协议

文章提出了一种估计的协议。 首先， 在第一阶段， 智能反射面保持不变的反射因子， 用户传输$B$个正交序列，基站接收到的信号可表示为下式：

$$\begin{array}{rl}{\mathbf{Y}}_b& =\sum _{k=1}^K{\mathbf{F}}^H\mathrm{diag}\left({\mathbf{v}}_b\right){\mathbf{h}}_k{\mathbf{s}}_k^H+{\mathbf{U}}_b\\ & \stackrel{(\mathrm{a})}{=}\sum _{k=1}^K{\mathbf{G}}_k^H{\mathbf{v}}_b{\mathbf{s}}_k^H+{\mathbf{U}}_b\end{array}$$

其中$U_b$为噪声， $s_k$为$k$个用户发送的导频序列。

最小二乘（LS）估计

文章先用了传统的LS估计。 由于假设每个用户发送的是正交序列， 即：$s_{k_1}^H{s}_{k_2}=0$ for $1\le k_1,k_2\le K$ and $k_1\ne k_2$，因此有：

${\tilde{\mathbf{y}}}_{b,k}\triangleq \frac{1}{PT}{\mathbf{Y}}_b{\mathbf{s}}_k={\mathbf{G}}_k^H{\mathbf{v}}_b+{\mathbf{u}}_{b,k}$

将多个用户的写到一起：

$${\tilde{\mathbf{Y}}}_k={\mathbf{G}}_k^H\mathbf{V}+{\tilde{\mathbf{U}}}_k$$

其中， $\mathbf{V}=\left[{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_B\right]$， ${\tilde{\mathbf{Y}}}_k=\left[{\tilde{\mathbf{y}}}_{1,k},{\tilde{\mathbf{y}}}_{2,k},\cdots ,{\tilde{\mathbf{y}}}_{B,k}\right]$, $B$是发送的训练序列数量。

那么这个的最小二乘解就是

$${\hat{G}}_k={\left({\tilde{\mathbf{Y}}}_k{\mathbf{V}}^{†}\right)}^H$$
其中， ${\mathbf{V}}^{†}={\mathbf{V}}^H{\left(\mathbf{V}{\mathbf{V}}^H\right)}^{-1}$。 这个解可以通过求导置为0得到。 而要使得${\left(\mathbf{V}{\mathbf{V}}^H\right)}^{-1}$有值，$\mathbf{V}$必须满足为列数>行数，这样才能满秩求逆。 因此， $B>L$， 即只有训练序列数大于智能反射面元件数时， 才能使用LS估计， 而这在$L$较大时，开销显然非常高昂。

信道的稀疏表示