基于智能反射面的MISO通信的最优波束赋形

《Optimal Beamforming for MISO Communications via Intelligent Reflecting Surfaces》
文章地址： https://arxiv.org/abs/2001.11429

问题背景

关于智能反射面的详细介绍可以参考https://zhuyulab.blog.csdn.net/article/details/103393524。仅以简略文字叙述。
为了满足高速率通信，无论是基于数模器件实现的MIMO通信还是基于智能反射面实现的MIMO通信，获得定向可控的波束-波束赋形是至关重要的环节。然而，相较于混合数模器件实现的波束赋形，由移相器和偶极子组成的智能反射面得益于其成本和功耗的特点，更具有潜力。因此，通过合理的设计使得智能反射面同样能够实现最优波束赋形值得深入地研究。

系统模型

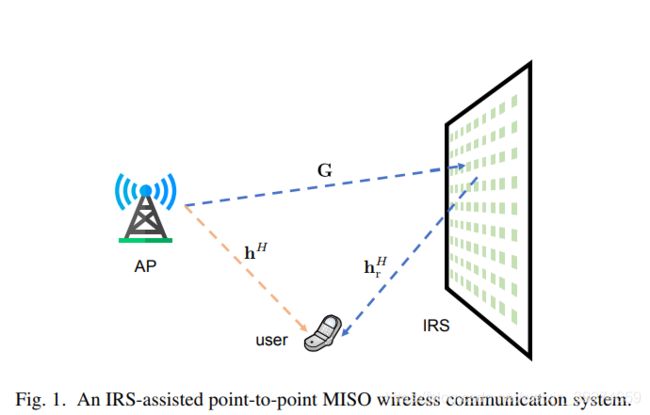
本文考虑的是一个IRS（Intelligent Reflecting Surfaces）协助的单用户MISO通信，如图所示：

图中，接入点AP配置有$N_{\mathrm{t}}$根天线，用户侧为单天线，智能反射面配置有$M$个可调的移相器。假设信道为准静态平稳衰落信道且假设在AP和IRS均已知信道状态信息（CSI）。因此，用户侧的接收信号可以表示为：
$$y=\left({\mathbf{h}}_{\mathrm{r}}^H\mathbf{\Phi }\mathbf{G}+{\mathbf{h}}^H\right)\mathbf{f}x+n$$
其中${\mathbf{h}}_{\mathrm{r}}\in {\mathbb{C}}^{M\times 1}$从IRS到用户的信道向量，$\mathbf{h}\in {\mathbb{C}}^{N_t\times 1}$是AP直接到用户的信道矩阵，AP到IRS的信道矩阵可以表示为$\mathbf{G}\in {\mathbb{C}}^{M\times N_t}$。在AP端的主动波束赋形矩阵和在IRS处的被动波束赋形矩阵分别表示为$\mathbf{f}\in {\mathbb{C}}^{N_{\mathrm{t}}\times 1}$和$\mathbf{\Phi }=\mathrm{diag}\left(e^{ȷ{\theta }_1},e^{ȷ{\theta }_2},\dots ,e^{ȷ{\theta }_M}\right)$，其中${\theta }_i$表示IRS中第$i$个移相器的相位，发送信号$x$满足$\mathbb{E}\left[|x{|}^2\right]=1$，$n$为方差为${\sigma }^2$的加性高斯白噪声。

问题描述

以频谱效率为目标，其可以表示为
$$R={\log }_2\left(1+\frac{{\left|\left({\mathbf{h}}_{\mathrm{r}}^H\mathbf{\Phi }\mathbf{G}+{\mathbf{h}}^H\right)\mathbf{f}\right|}^2}{{\sigma }^2}\right)$$
通过IRS实现最优波束赋形来最大化频谱效率，因此最终的优化问题可以表示为：
$$\begin{array}{ll}\underset{\mathbf{f},\mathbf{\Phi }}{\mathrm{maximize}}& {\left|\left({\mathbf{h}}_{\mathbf{r}}^H\mathbf{\Phi }\mathbf{G}+{\mathbf{h}}^H\right)\mathbf{f}\right|}^2\\ \text{ subject to }& \Vert \mathbf{f}{\Vert }_2^2\le P\\ & \mathbf{\Phi }=\mathrm{diag}\left(e^{ȷ{\theta }_1},e^{ȷ{\theta }_2},\dots ,e^{{ȷ}^{g}M}\right)\end{array}$$
其中，$P>0$为给定的最大传输功率。
首先关注被动波束赋形$\mathbf{\Phi }$的求解，上述的问题可以重新表示为问题${\mathcal{P}}_1$，即：
$$\begin{array}{rl}& \underset{\mathbf{v}\in {\mathbb{C}}^{M+1}}{\mathrm{minimize}}f(\mathbf{v})={\mathbf{v}}^H\mathbf{R}\mathbf{v}\\ & \text{ subject to }\left|v_i\right|=1,i=1,2,\dots ,M+1\end{array}$$
其中，$\mathbf{v}={\left[{\mathbf{x}}^T,t\right]}^T,\mathbf{x}={\left[e^{j{\theta }_1},e^{j{\theta }_2},\dots ,e^{j{\theta }_M}\right]}^H,t\in \mathbb{C}$,

$$\mathbf{R}=-\left[\begin{array}{cc}\mathrm{diag}\left({\mathbf{h}}_{\mathrm{r}}^H\right)\mathrm{G}{\mathbf{G}}^H\mathrm{diag}\left({\mathbf{h}}_{\mathrm{r}}\right)& \mathrm{diag}\left({\mathbf{h}}_{\mathrm{r}}^H\right)\mathrm{G}\mathrm{h}\\ {\mathbf{h}}^H{\mathbf{G}}^H\mathrm{diag}\left({\mathbf{h}}_{\mathrm{r}}\right)& 0\end{array}\right]$$
注意到：$t$引入的辅助变量。因此，当得到了最优的$\mathbf{v}$可以将其前$M$个元素恢复为最优被动波束赋形矩阵$\mathbf{\Phi }$。对于主动波束赋形矩阵$\mathbf{f}$，根据最大速率传输策略（MRT），$\mathbf{f}$的解为：
$$\mathbf{f}=\sqrt{P}\frac{{\mathbf{G}}^H\mathrm{diag}\left({\mathbf{h}}_{\mathbf{r}}\right)\mathbf{x}+\mathbf{h}}{{\Vert {\mathbf{G}}^H\mathrm{diag}\left({\mathbf{h}}_{\mathbf{r}}\right)\mathbf{x}+\mathbf{h}\Vert }_2}$$

• 对于问题${\mathcal{P}}_1$，$\mathbf{R}$非正定矩阵，且约束条件含有恒模约束，这些都使得问题高度非凸。总之，${\mathcal{P}}_1$是一个搜索维度为$M+1$的NP-hard问题。
• 采用半正定松弛（SDR）的方法可以处理问题${\mathcal{P}}_1$，其中辅助变量$\mathbf{V}=\mathbf{v}{\mathbf{v}}^H$被引入将${\mathcal{P}}_1$重新表示为一个带有额外秩1约束的半正定规划（SDP）问题。然后，释放秩1约束，使用凸优化的方法就可以很好地求解SDP问题，但并不能保证所得到$\mathbf{V}$满足秩1条件，采用高斯随机方法可以保证其渐进最优。因此，SDR方法提供了$\mathbf{v}$的一个近似解.
• 采用流行优化的方法可以获得问题${\mathcal{P}}_1$的一个局部最优解.，即使如此，其性能十分优秀。在这篇论文中，作者提出了分支界定法来得到${\mathcal{P}}_1$的全局最优解并研究了流行优化方法的最优度。

分支界定算法

在最优化理论中，分支界定算法（Branch-and-Bound, BnB）通常是用于求解离散组合优化问题，它通过树遍历的方法对候选解进行系统的枚举。简要阐述其基本原理：在搜索树中，每一个节点与一个集合相关，该集合是求解问题所定义的可行集中的一个子集。对于每一个节点，用相应的子集来表示一个子问题，并给出其上界和下界来估计该子问题的最优解。在BnB算法的每一次迭代中，根据节点选择规则选择一个节点，该规则通常与边界相关。然后，将选择的节点(关联集)进一步分支为两个子节点(子集)。.随着树结构的不断增长，可行集被逐步分割成目标值改进后的更小的子集。最近它也被用于了连续优化问题的求解当中。特别是，遵循BnB原则，在每次迭代中更新所选子问题的边界，直到收敛，即:，上界和下界的差为0。总而言之，对于BnB算法，有三个至关重要的因素需要精心设计：1.针对分支的选择节点 2.剪枝规则 3.边界函数。

下界与上界

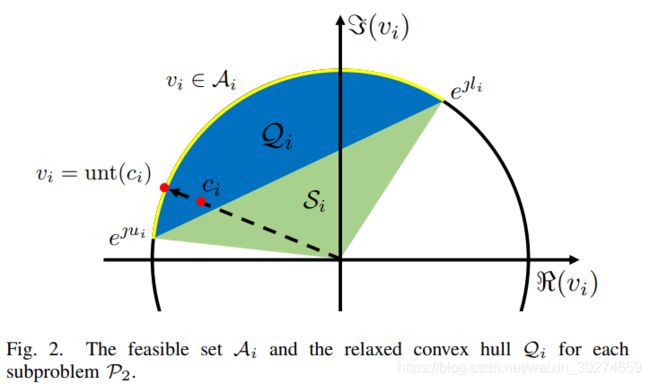
问题${\mathcal{P}}_1$的可行集是$M+1$个单位圆的乘积。因此，对于搜索树，与任意一个节点相关的子集可以定义为：$\mathcal{A}={\prod }_{i=1}^{M+1}{\mathcal{A}}_i,i=1,2,\dots ,M+1$，${\mathcal{A}}_i$表示端点分别$e^{j{l}_i}$和$e^{j{u}_i}$的一段圆弧，参照图2的黄色圆弧，其中$l_i$和$u_i$分别为$\mathbf{v}$的第$i$个元素参数区间的极限点。在BnB算法的每一次迭代中，一旦一个节点被选择，则${\mathcal{P}}_1$的子问题${\mathcal{P}}_2$表示为：

$$\begin{array}{rl}& \underset{\mathbf{v}\in {\mathbb{C}}^{M+1}}{\mathrm{minimize}}f(\mathbf{v})={\mathbf{v}}^H\mathbf{R}\mathbf{v}\\ & \text{ subject to }{v}_i\in {\mathcal{A}}_i,\forall i\end{array}$$

通过定义$\mathbf{V}=\mathbf{v}{\mathbf{v}}^H$，子问题${\mathcal{P}}_2$等价于问题${\mathcal{P}}_3$，即：

$$\begin{array}{cl}\underset{\mathbf{v},\mathbf{V}⪰0}{\mathrm{minimize}}& \underline{g}(\mathbf{V})=\mathrm{tr}(\mathbf{R}\mathbf{V})\\ \text{ subject to }& v_i\in {\mathcal{A}}_i,\forall i\\ & \mathrm{Diag}(\mathbf{V})=1_{M+1}\\ & \mathbf{V}=\mathbf{v}{\mathbf{v}}^H\end{array}$$

根据BnB准则，为了求解${\mathcal{P}}_1$，问题${\mathcal{P}}_3$的上界和下界需要被推导，更重要地是，这两个界越紧，则算法收敛速度越快。接下来的任务就是为问题${\mathcal{P}}_3$寻找紧界。

首先，放松秩1约束，即：$\mathbf{V}⪰\mathbf{v}{\mathbf{v}}^H$ , 它表示$\left|v_i\right|\le 1$，对于$i=1,...,M+1$。此时的放松后的可行集变为了由${\mathcal{A}}_i$所定义的扇形区域，也就是图二中的${\mathcal{Q}}_i\cup {\mathcal{S}}_i$。然而，该扇形区域并不是问题${\mathcal{P}}_3$中可行集${\mathcal{A}}_i$最紧的凸松弛， 图中的${\mathcal{Q}}_i$（即圆弧和弦所围成的区域）为最紧的凸松弛。因此，对于问题${\mathcal{P}}_3$的一个紧下界可以通过求解问题${\mathcal{P}}_4$获得，即：
$$\begin{array}{cl}\underset{\mathbf{c},\mathbf{C}⪰0}{\mathrm{minimize}}& \underline{g}(\mathbf{C})=\mathrm{tr}(\mathbf{R}\mathbf{C})\\ \text{ subject to }& c_i\in {\mathcal{Q}}_i,\forall i\\ & \mathrm{Diag}(\mathbf{C})=1_{M+1}\\ & \mathbf{C}⪰\mathbf{c}{\mathbf{c}}^H\end{array}$$

对于问题${\mathcal{P}}_4$的第一个约束可以重新表示为：
$$\Re \left({\mathbf{a}}^{\ast }\circ \mathbf{c}\right)\ge \cos \left(\frac{\mathbf{u}-1}{2}\right)$$

根据Schur补的关系，${\mathcal{P}}_4$的最后一个约束等价为：
$$\left[\begin{array}{cc}1& {\mathbf{c}}^H\\ \mathbf{c}& \mathbf{C}\end{array}\right]⪰0$$

前面那么多的数学化简，均是为了将问题${\mathcal{P}}_4$化为标准凸优化问题的形式，然后使用CVX的工具进行求解。

关于上界：将问题${\mathcal{P}}_4$的最优解投影到${\mathcal{P}}_3$的可行域上，然后上界由$f\left(\mathbf{v}\right)$给出。相当于取相位然后限制恒模的操作。

节点选择和剪枝规则

选择具有更小下界的节点，根据问题${\mathcal{P}}_4$的解$\mathbf{c}$和它的投影解$\mathbf{v}$之间的欧式距离对其相关的可行集$\mathcal{A}$进行均等划分其。具体说来，均分${\mathcal{A}}_{i^{\star }}$，保持${\mathcal{A}}_i$（$i\ne i^{\star }$）不变，其中
$$i^{\star }=\arg \underset{i}{\max }\left|c_i-v_i\right|$$
综上所述，上下界，节点的选择与剪枝规则均已确定，设置一个收敛容忍度$ϵ$就可以获得一个最优解。
文中给出了具体的伪代码。

关于收敛性分析具体参照原文，不再叙述。

仿真分析

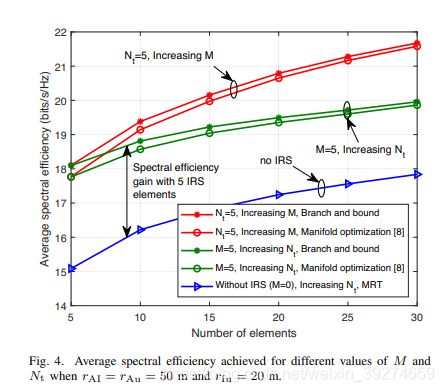
图中蓝色的线表示无IRS被动波束赋形时仅有基于MRT策略的主动波束赋形传输时的AP端天线数目与频谱效率的关系图，红线分别表示使用BnB算法和MO算法时IRS可配置移相器数目与频谱效率的关系图，绿线分别表示AP端天线数目与频谱效率的关系图。
仿真图的结论如下：

• 对于频谱效率的提升，增加IRS可配置移相器的数目比增加AP天线数目更加有效，并且随着天线规模的数目增多，其带来的能源开销相较于无源的IRS是十分明显的。
• BnB算法可以作为现存次优算法的一个性能基准。
• MO算法是设计IRS协助MISO通信的一个有效算法，能够很好地逼近BnB算法。