python可视化(2-1)绘图对象(条形图、直方图、柏拉图)
刚上班那会,从室友那里不经意拿到一本刘万祥老师的《Excel图表之道》,相信有很多读者也都阅读过那本书,作为可视化领域鼻祖类的书籍,该书给了我不少体会:
体会一:图表应该是不需要解释的,或者说是自我解释的,所谓“一图抵千言”
体会二:看起来好看的图表都是很多元素堆积起来的,在没有使用代码的情况下,刘万祥老师巧妙地通过表格、图像元素,“重现出”经济学人等杂志的图,实属不易。
体会三:根据数据类型及数据关系,寻找到恰当的绘图对象,是说好故事的关键
Excel是很出色的工具,不需要编写代码,带有按钮的界面也很有亲和力,操作实时更新、调整实时同步。那为什么还要写代码呢?原因很多,但最为重要的恐怕就是效率,事实上Excel调好一张图也并不那么容易,需要操作按钮的次数远比写入代码的字符数多,且复用性不好;另一方面,在处理截面数据(特征数据,类似数据库样式的结构化数据)时,代码会更高效,很多语言都提供了现成的接口对数据进行聚合、排序、分组、去重、过滤等,相同的操作在Excel中可能需要增加不少辅助列或者生成大量的临时表;再就是如果某一项工作内容需要高频地重复做,这时候选择代码最适合不过,将业务流程固化到代码后可以将数据数据和可视化两步合成一步,每次任务只需要替换数据源就可达到相同目的,大大提高了工作效率。从入门篇想必大家也看到了,python的代码是非常简洁的,只用了很少行的代码就实现了正弦曲线的绘制,并为图像增加了很多元素,但这远远不够,可视化是为了更好地说明问题、阐述事实、描绘数据,选择恰当的图表对象,配之以恰当的区分(可以是颜色、线条样式、标记图案等),说好数据里面的故事,窃以为是可视化真正的核心。因此入门篇完成之后,会花比较大的篇幅把matplotlib中的基础绘图对象尽可能细致地过一遍。
matplotlib的基础绘图对象有很多,如柱形图、直方图、箱线图、折线图、散点图等,他们提供了用以可视化的最底层接口。正因为是最底层的,因此想要达到作者的预期效果,需要调整的参数常常就较多,为此pandas、seaborn等库就在matplotlib的基础上进行了封装,只需要很少的代码就能实现底层接口N多行代码才能实现的效果。但万丈高楼平地起,最为原始的,往往力量是最大的,自由度也是最高的,换句话说,深入理解了基础库的基础接口,对封装库的使用才能得心应手。
本文重点介绍条形图、直方图
文章目录
- 条形图
-
- plt.bar
- 简单修饰
- 堆积图
- 横向堆积图
- 条形图原理
- 制作二维码
- 横向条形图
- 项目进度图-甘特图
- 带误差线的条形图
- 误差线图
- 直方图
-
- 等分直方图
- 自定义分组直方图
- 累积分布直方图
- 概率密度直方图
-
- 直方图轮廓线填充方式
- 累积概率密度直方图
- 概率密度曲线图
- 累积概率密度曲线图
- 联合概率密度分布图
- 带权重系数的直方图-柏拉图
本文的运行环境为 jupyter notebook
python版本为3.7
本文所用到的库包括
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
条形图
条形图的基础接口为 plt.bar,
很简单,只需要1行代码就能完成条形图的绘制,x为柱子的位置,height为柱子的高度。
plt.bar
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
height = [1, 1, 2, 2, 3, 2, 2, 1, 1]
plt.bar(x=x, height=height)
简单修饰
绘制出来的条形图,颜色、间距、填充都使用默认参数,可以通过具体参数对其进行修改
x = [1, 2, 3, 4, 5, 6, 7, 9, 10]
height = [1, 1, 2, 2, 3, 2, 2, 1, 1]
plt.bar(x=x,
height=height,
width=0.7, # 柱子与柱子的间隔,如width=1,表示柱子与柱子完全紧挨
fill=True, # fill默认为True,表示每个柱子都可以填充颜色
hatch='/', # 纹理填充
facecolor='skyblue',# 当fill为True时,柱子填充颜色
edgecolor='black', # 轮廓及填充纹理的线条颜色
ls='-', # linestyle 轮廓线线型
lw=1.5,) # linewidth 线宽
堆积图
有时候,我们需要绘制堆积起来的条形图,可通过参数bottom进行修改
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
height1 = [1, 1, 2, 2, 3, 2, 2, 1, 1]
height2 = [3, 2, 1, 2, 2, 1, 2, 2, 1]
height3 = [1, 1, 1, 2, 2, 1, 1, 1, 1]
plt.bar(x=x,height=height1)
plt.bar(x=x,height=height2,bottom=height1)
plt.bar(x=x,height=height3,bottom=np.array(height1)+np.array(height2))
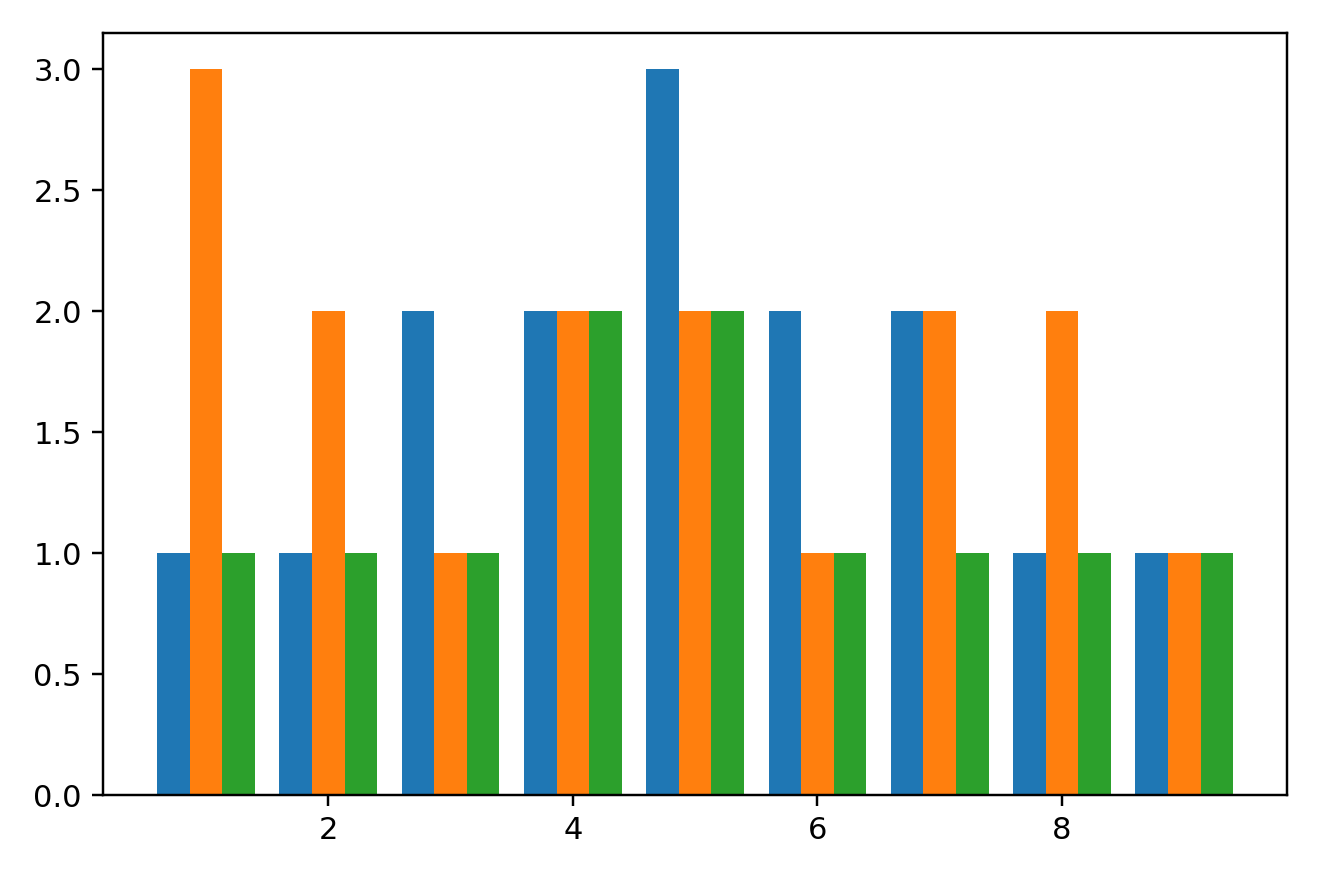
横向堆积图
当我们需要并列地展示各个数据序列的时候,可以通过width参数的调节来实现,原理是通过调节每个序列数据的x坐标及柱宽两个参数。
如本例中将height1序列所有x坐标向左移动1/3柱宽(width),height3序列所有x坐标向右移动1/3柱宽(width),且将三个序列的柱宽均设置为1/3(width),即实现了横向堆积的效果。
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
height1 = [1, 1, 2, 2, 3, 2, 2, 1, 1]
height2 = [3, 2, 1, 2, 2, 1, 2, 2, 1]
height3 = [1, 1, 1, 2, 2, 1, 1, 1, 1]
width = 0.8
plt.bar(x=np.array(x) - width/3, height=height1, width=width/3)
plt.bar(x=np.array(x), height=height2, width=width/3)
plt.bar(x=np.array(x) + width/3, height=height3, width=width/3)
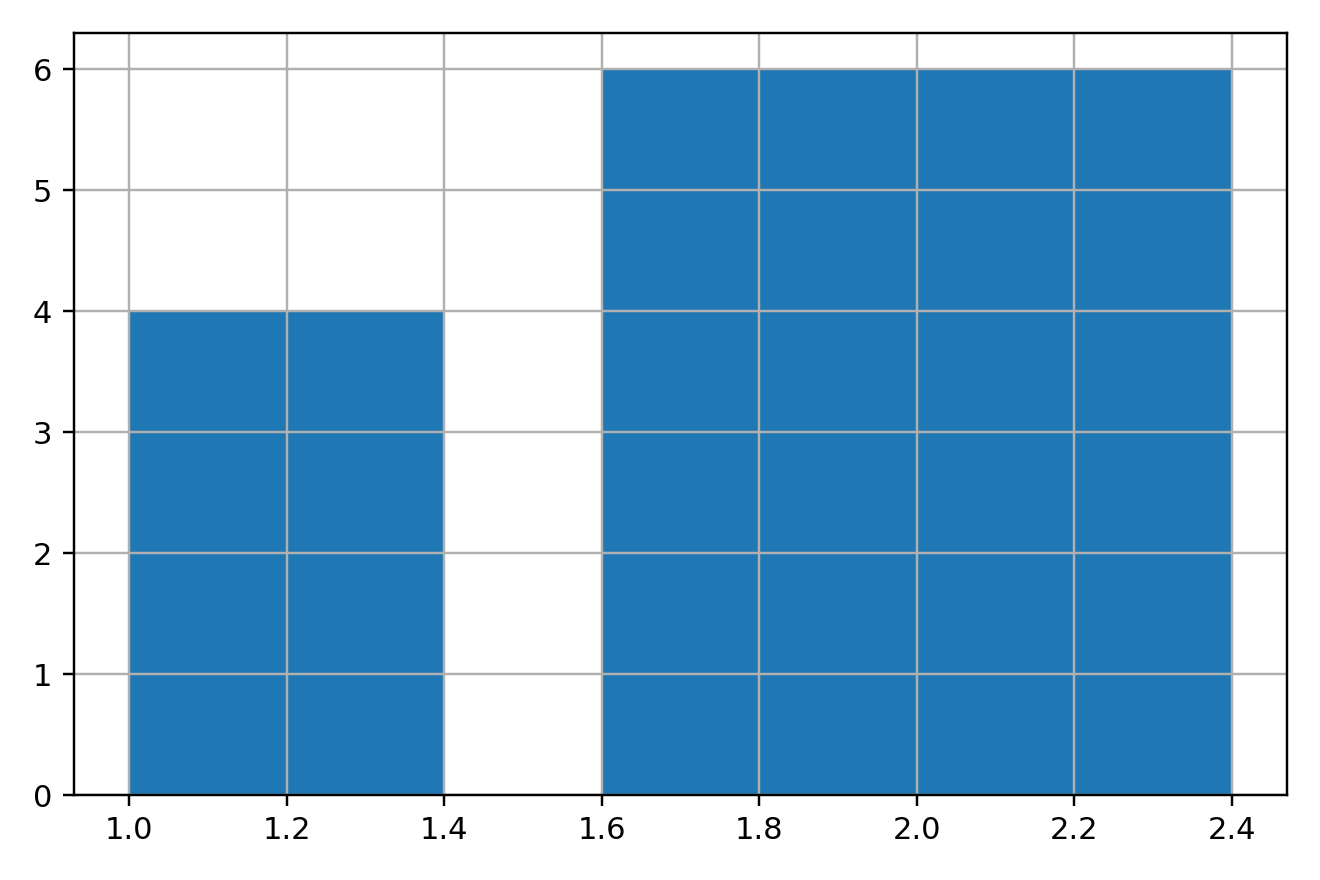
条形图原理
有必要总结一下,x,height,width是条形图最为重要的3个参数。条形图是以x数值为中心,在向左和向右各1/2width的区域内绘制一个高度为height的柱子,下图形象地说明了这个原理。矮柱子绘制的区间范围为**[1.2-1/2×0.4,1.2+1/2×0.4],即[1.0,1.4],高柱子绘制的区间范围为[2.0-1/2×0.8,2.0+1/2×0.8],即[1.6,2.4]**。
从本例可以看出,参数 x,height,width 都是可以接受列表(或数组)对象的。这么设计的好处,自然是使得对图对象的调整更自由,这就是熟悉底层接口的好处。
对于柱中心点的位置,需要说明的是,接口中align参数默认为’center’,即柱子中心落在x坐标,如该参数设置为’edge’ ,柱子左侧边缘则会恰好落在x位置,读者可自行调试观察。
x = [1.2, 2.0]
height = [4.0, 6.0]
width = [0.4, 0.8]
plt.bar(x=x, height=height, width=width) # width可接受向量或者标量形式传入
plt.grid()
制作二维码
巧妙地传入x和width参数,可以绘制一个类似二维码的图像。
为了便于读者复现,代码第一行通过numpy指定了随机数种子。
np.random.seed(121)
fig=plt.figure(figsize=(6,3)) # 图片宽度和高度
N = 80
x = np.linspace(0, N, N) # 在0-N区间,均匀生成 N 个数据点
height = np.ones(shape=(N,)) # 生成长度为N,数据均为1的向量
width = np.random.uniform(0, 1, N) # 随机生成N个在0-1区间的小数,该小数即为柱子的列宽
plt.bar(x=x, height=height, width=width, facecolor='black')
plt.axis('off') #去除边框
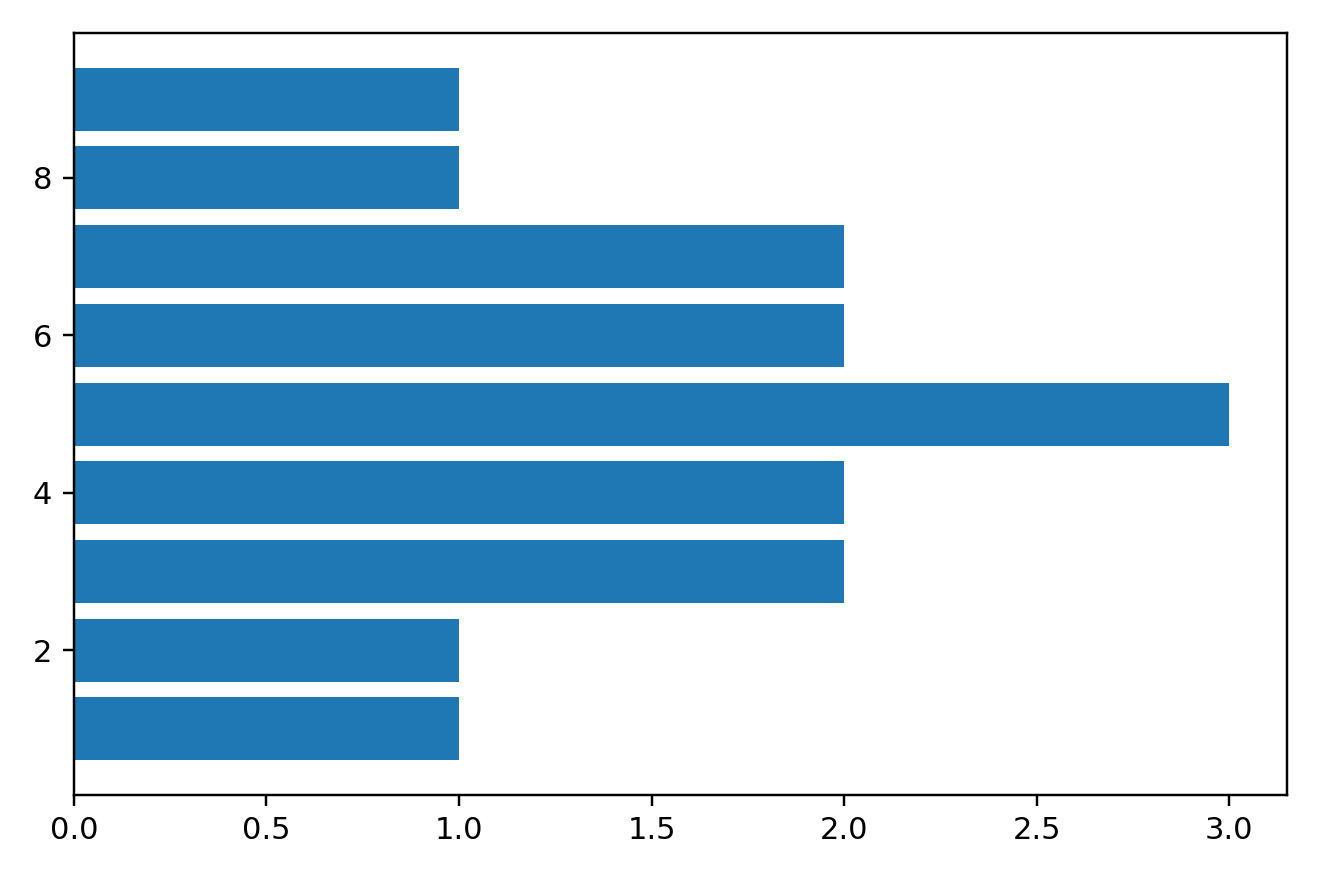
横向条形图
水平方向的条形图与垂直方向的参数大致相同。如下图,只需要一行代码即可生成一张水平方向的条形图。
y = [1, 2, 3, 4, 5, 6, 7, 8, 9]
width = [1, 1, 2, 2, 3, 2, 2, 1, 1]
plt.barh(y=y, width=width)
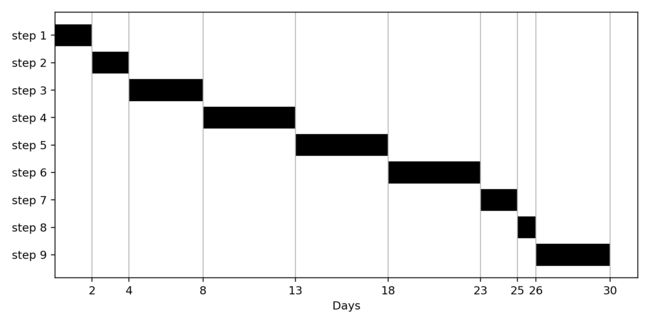
项目进度图-甘特图
通过堆积参数设置(plt.bar接口通过bottom参数传递底部堆积序列,plt.barh通过left参数传递左侧堆积序列数据)、y轴标签文本设置、x轴标签位置设置及网格线设置,plt.barh可以用很少的代码完成项目管理中常用的甘特图的绘制。
fig=plt.figure(figsize=(8,4))
steps = [9, 8, 7, 6, 5, 4, 3, 2, 1]
tick_label = ['step %s' % (i+1) for i in range(9)] # y轴轴标签文字
days = [2, 2, 4, 5, 5, 5, 2, 1, 4]
predays = np.append(0, np.cumsum(days)[:-1])
# predays 表示在某一step 下,该step之前累计消耗天数 [0, 2, 4, 8, 13, 18, 23, 25, 26]
plt.barh(y=steps, width=days, left=predays,
tick_label=tick_label, fc='black') # fc:facecolor
plt.xlabel('Days')
plt.xticks(ticks=np.cumsum(days))
# np.cumsum(days): 返回 days列表的累积和 [ 2 4 8 13 18 23 25 26 30]
plt.grid(axis='x')
#只显示x轴刻度所对应网格线
带误差线的条形图
当我们需要标注数据在柱顶附近偏离情况的时候,可以通过yerr参数传入误差范围,并通过capsize调节误差线两端短横线的宽度。
yerr传入的数据类型如为标量,如0.2,则表示每个柱子的正负误差均为0.2;如为(1,N)列表,如[0.1, 0.2, 0.4, 0.2, 0.3, 0.2, 0.2, 0.2, 0.4],则表示,为每一个柱子分别指定了不同的正负误差,且正负误差的绝对值相等;如为(2,N)列表,则列表中第一个元素表示每个柱子对应的负误差绝对值,第二个元素表示每个柱子对应的正误差绝对值,如本例。
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
height = [1, 1, 2, 2, 3, 2, 2, 1, 1]
yerr = [[0.2]*9, # 负误差为0.2
[0.3]*9] # 正误差为0.3
plt.bar(x=x,
height=height,
fill=False,
yerr=yerr,
capsize=4)
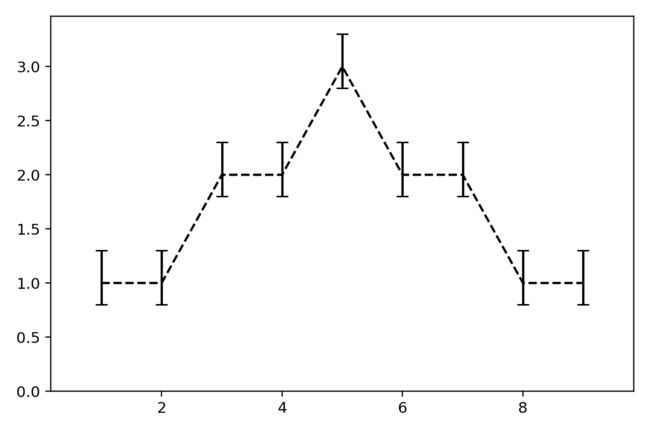
误差线图
显然,我们只需要将轮廓线设置为白色,且增加一条趋势线,条形图就几乎完美地变成了一张误差线图。
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
height = [1, 1, 2, 2, 3, 2, 2, 1, 1]
yerr = [[0.2]*9,
[0.3]*9]
plt.plot(x,height,c='black',ls='--') #增加趋势线
plt.bar(x=x,
height=height,
fill=False,
edgecolor='white', #将柱形图的边框调整为白色
yerr=yerr,
capsize=4)
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
y = [1, 1, 2, 2, 3, 2, 2, 1, 1]
yerr = [[0.2]*9,
[0.3]*9]
plt.errorbar(x=x,y=y,yerr=yerr)
直方图
因为都是柱子形状的,因此直方图常与条形图傻傻分不清楚。尤其对于Excel而言,是没有直方图这个对象的。
两者最大的区别在于:直方图描述的是随机变量的分布情况,其原理是将随机变量按区间切分成小组(bins),在每个小组进行频数或者概率密度的统计,从表述可以看出,直方图是更侧重变量统计意义的,而条形图更侧重用来展示一种对比关系。
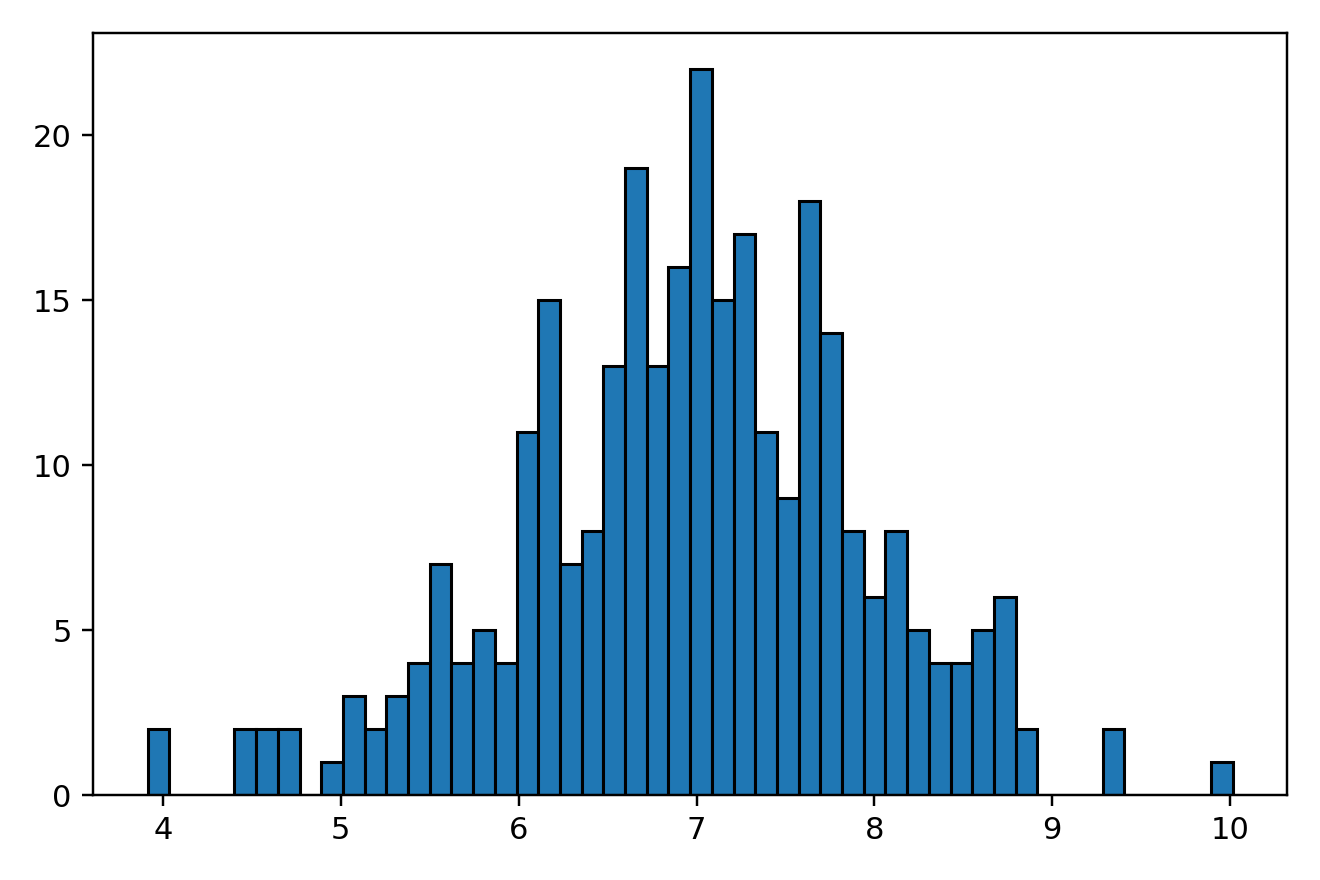
等分直方图
将300个中心值为7.0,标准偏差为1.0的数据,均分为50个小组(细心的小伙伴可能数了一遍发现并不是50个柱子,原因是有些区间没有数据分布,频数为0,因此不显示柱子),其频数分布如下图所示:
np.random.seed(121)
x=np.random.normal(loc=7.0,scale=1.0,size=300)
plt.hist(x,bins=50,ec='black') # ec:edgecolor bins:数据被均分为多少子集
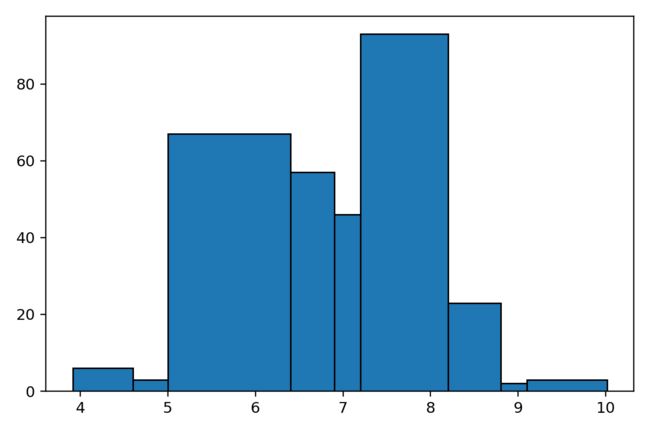
自定义分组直方图
我们也可以自定义数据区间对数据进行切分,从而统计各区间小组(bins)的频数值。如下图所示,数据落在区间[7.2,8.2]最多。
np.random.seed(121)
x = np.random.normal(loc=7.0, scale=1.0, size=300)
bins = [x.min(),4.6, 5.0, 6.4, 6.9, 7.2, 8.2, 8.8, 9.1,x.max()]
plt.hist(x, bins=bins, ec='black') # bins 数据根据bins划分为区间
累积分布直方图
可以通过调节参数cumulative,绘制累积分布的直方图,cumulative默认为False
np.random.seed(121)
x = np.random.normal(loc=7.0, scale=1.0, size=300)
bins = [x.min(), 4.6, 5.0, 6.4, 6.9, 7.2, 8.2, 8.8, 9.1, x.max()]
plt.hist(x, bins=bins, cumulative=True, ec='black') # bins 数据根据bins划分为区间
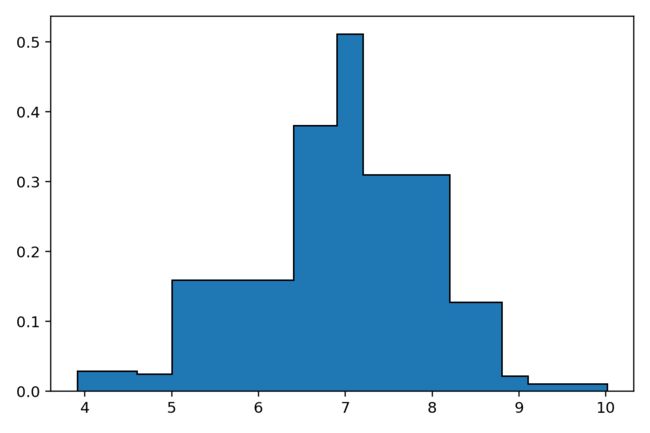
概率密度直方图
可以通过调节参数density,将y轴的频数变成概率密度,density默认为False
不知道大家是否看出表示概率密度的直方图与表示频数分布的直方图的区别。在频数图上[7.2,8.2]区间柱子的高度最高,通过代码 np.sum(x[x>=7.2]<=8.2) 可以统计出其区间内共有93个数据点;而在概率密度图上,其高度并不是最高,这是为什么呢?因为在概率密度图上是以面积来计算该区间数据占比比例的,同样以[7.2,8.2]区间为例,柱子的宽为 8.2-7.2=1.0 ,高大约为0.31(目测,虽然目测地很准~~),则该区域对应的图面积为 1.0×0.31×100%=31%,该数据与 93/300×100%=31%是一致的(300为总的数据点个数)。
np.random.seed(121)
x = np.random.normal(loc=7.0, scale=1.0, size=300)
bins = [x.min(), 4.6, 5.0, 6.4, 6.9, 7.2, 8.2, 8.8, 9.1, x.max()]
plt.hist(x, bins=bins, density=True, ec='black') # bins 数据根据bins划分为区间
直方图轮廓线填充方式
通过调节参数histtype,可以去除图像内部的轮廓线,只保留最外层。当histtype='step’时,则只保留外部轮廓线,不填充。
np.random.seed(121)
x = np.random.normal(loc=7.0, scale=1.0, size=300)
bins = [x.min(), 4.6, 5.0, 6.4, 6.9, 7.2, 8.2, 8.8, 9.1, x.max()]
plt.hist(x, bins=bins, density=True, ec='black', histtype='stepfilled')
累积概率密度直方图
density, cumulative两个参数均为True时,此时为累积概率密度直方图,可以看到最后一个值时,y坐标为1。
np.random.seed(121)
x = np.random.normal(loc=7.0, scale=1.0, size=300)
bins = [x.min(), 4.6, 5.0, 6.4, 6.9, 7.2, 8.2, 8.8, 9.1, x.max()]
plt.hist(x, bins=bins, density=True, cumulative=True,ec='black')
概率密度曲线图
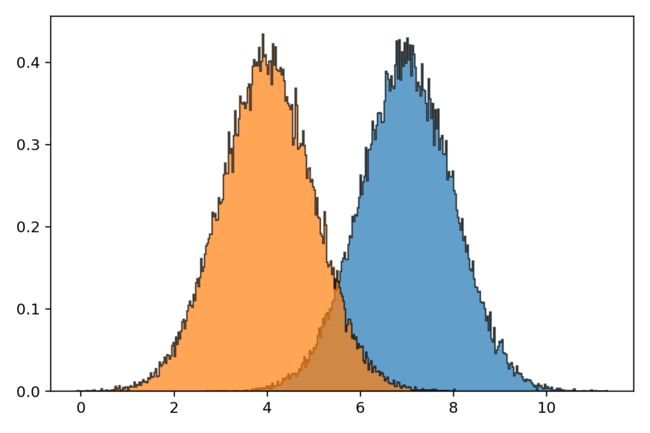
以下代码模拟了,无限多(50000个)随机生成的正态分布数据在切成足够多小块(bins=300)时,其数据分布将无限接近标准正态分布曲线。
np.random.seed(121)
x1 = np.random.normal(loc=7.0, scale=1.0, size=50000)
x2 = np.random.normal(loc=4.0, scale=1.0, size=50000)
plt.hist(x1, bins=300, density=True,ec='black',histtype='stepfilled',alpha=0.7) # histtype, step,stepfilled,bar,barstacked
plt.hist(x2, bins=300, density=True,ec='black',histtype='stepfilled',alpha=0.7)
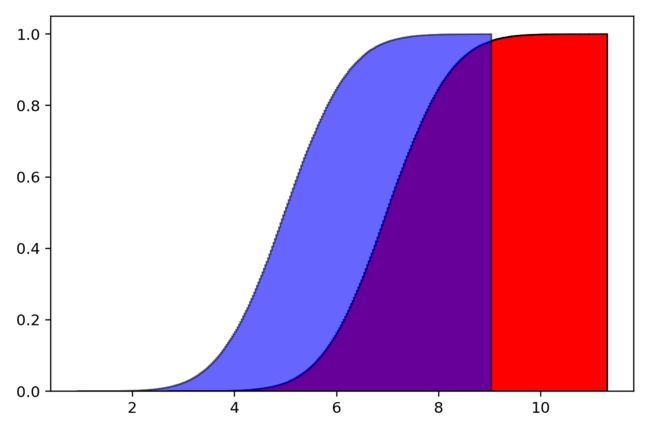
累积概率密度曲线图
显然,其累积概率密度曲线也是十分的优雅。
np.random.seed(121)
x1 = np.random.normal(loc=7.0, scale=1.0, size=50000)
x2 = np.random.normal(loc=5.0, scale=1.0, size=50000)
plt.hist(x1, bins=300, density=True, cumulative=True, color='red',
ec='black', histtype='stepfilled')
plt.hist(x2, bins=300, density=True, cumulative=True, color='blue',
ec='black', histtype='stepfilled', alpha=0.6)
联合概率密度分布图
当我们需要研究两个不同分布的随机变量的关系时,可以通过plt.hist2d接口绘制联合概率密度分布图,图通过颜色渐变表现联合分布的密度大小,本图中越接近黄色部分,说明数据分布密度越大。这不就是宇宙大爆炸时候的样子嘛。
np.random.seed(121)
x = np.random.normal(loc=4.0, scale=1.0, size=500000)
y = np.random.normal(loc=3.0, scale=1.0, size=500000)
xy_range=[[2,6],[0,6]] # x ± 2sigma, y ± 3sigma,
plt.hist2d(x,y,density=True,bins=100,range=xy_range,cmap=plt.cm.hot)
带权重系数的直方图-柏拉图
人的一生是怎样度过的
人的一生的时间分配:
据研究人员估算是这样的
以70岁的划算-------
站立:30年。
睡、卧:23年。
坐:17年。
走路:16年。
劳动:10–12年。
在饭桌:6年。
用在等车:3–6年。
交谈:2年。
看电视:约6年。
——[摘自《现代女报》]
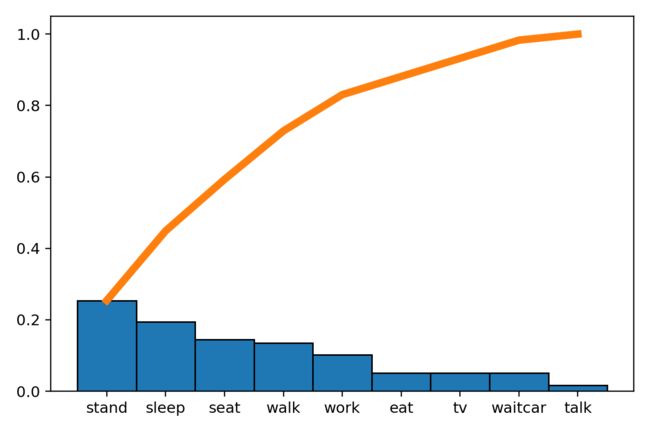
下面的代码和绘图,或许是这首小诗贴切的表达,这个图有一个专门的名字——柏拉图。
labels = ['stand', 'sleep', 'seat', 'walk',
'work', 'eat', 'tv', 'waitcar', 'talk']
weights = [30, 23, 17, 16, 12, 6, 6, 6, 2]
x=np.arange(1,10)
plt.hist(x, weights=weights, bins=np.arange(1,11), align='left',density=True,ec='black')
plt.plot(x,np.cumsum(weights)/np.sum(weights),lw=5) # lw:linewidth
plt.xticks(ticks=x,labels=labels) #替换x坐标数值为对应单词
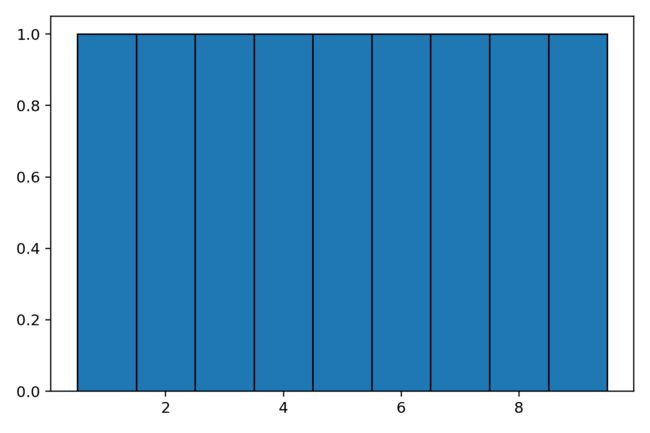
显然,如果每件事都没有了权重(weights),人生就该是如下图一般的平静。
x = np.arange(1, 10)
plt.hist(x, bins=np.arange(1, 11), align='left',ec='black') # 没有weights的时候,x是均匀分布的
以上!