EfficientNet论文翻译
原文链接:https://arxiv.org/abs/1905.11946
文章目录
-
- 摘要
- 介绍
- 相关工作
- 复合模型缩放
-
- 问题公式化
- 缩放维度
- 复合缩放
- EfficientNet 结构
- 实验
-
- 放大MobileNets和ResNets
- EfficientNet在ImageNet上的结果
- EfficientNet迁移学习的结果
- 讨论
- 总结
- 参考
摘要
卷积神经网络(ConvNets)普遍在一个固定的资源预算下发展的,如果可以获得更多的资源那么就增大模型来得到更好的准确率。本文系统性的研究了模型缩放尺度和以及确认,仔细地平衡网络的深度,宽度,和分辨率能够得到更好的效果。基于这个观点,我们提出了一个新的尺度缩放的方法,统一地缩放所有的维度,深度/宽度/分辨率使用一个简单且高效的复合系数。我们通过增大MobileNets和ResNet来证明这个方法的有效性。
为了进一步的证明,我们使用神经网络结构搜索去设计一个新的baseline网络并且对其进行放大进而获得一个模型家族,叫做EfficientNets,达到了比之前的ConvNets更好的准确率和效率。尤其是我们的EfficientNet-B7在ImageNet上达到了最好的水平即top-1准确率84.4%/top-5准确率97.1%,然而却比已有的最好的ConvNet模型小了8.4倍并且推理时间快了6.1倍。我们的EfficientNet迁移学习的效果也好,达到了最好的准确率水平CIFAR-100(91.7%),Flowers(98.8%),和其他3个迁移学习数据集合,参数少了一个数量级。
代码:
- 官方代码
- Pytorch 亲测好用
介绍
增大ConvNets被广泛的使用来达到更好的准确率。例如ResNet(He et al.)能够从ResNet-18通过使用更多的层来放大到ResNet-200;最近GPipe(Huang et al.,2018)通过增大一个baseline模型四倍,在ImageNet上top-1准确率达到了84.3%。然而,ConvNets增大的过程一直没有被很好的理解而且目前有很多种方法来做这件事情。最常用的做法是放大ConvNets的深度(He et al.,2016)或宽度(Zagoruyko & Komodakis,2016)。另一个不太常用的但是也越来越普及的方法是通过增加图像的分辨率来增大模型。在之前的工作中,通常只是放大三个维度-深度,宽度,和图像尺寸中的一个维度。尽管可以任意地增大两个或三个维度,但任意的增大需要枯燥的手工调参并且还经常产生次好的准确率和效率。
这篇文章中,我们想要研究和重新思考下ConvNets放大的过程。尤其是我们研究了这个核心问题:是否有一个原则性的方法来增大ConvNets能够达到更好的准确率和效率呢?我们的经验研究表明,平衡网络所有维度宽度/深度/分辨率是决定性的,而令人惊讶的是这样的平衡能够通过一个常数比例来简单地增大每个维度达到。基于这个观点,我们提出了一个简单且有效的复合增大的方法。不像传统的做法任意的增大这些因子,我们的方法通过一个固定的增大系数的集合来一致地增加网络的宽度,深度和分辨率。例如,如果我们想要使用 2 N 2^N 2N倍的更多计算资源,那么我们可以通过 α N \alpha^N αN来增加网络的深度,通过 β N \beta^N βN增加网络的宽度,通过 γ N \gamma^N γN来增加图片的尺寸,其中 α , β , γ \alpha,\beta,\gamma α,β,γ是通过在原始小模型上使用一个小格子搜索决定的常数系数。图2阐明了我们的增大方法和传统方法间的差距。

直观地,这种复合增大的方法是有意义的因为如果输入图像是更大的话,那么网络需要更多的层来增加感受野并且也需要更多的通道在更大的图像上捕捉更细粒度的图案。事实上之前的理论(Raghu et al., 2017; Lu et al., 2018)和经验结果(Zagoruyko & Konodakis,2016)都显示了网络的宽度和深度是存在确定关系的,但据我们所知,我们是第一个经验的量化三个维度间的关系,网络的宽度,深度和分辨率。
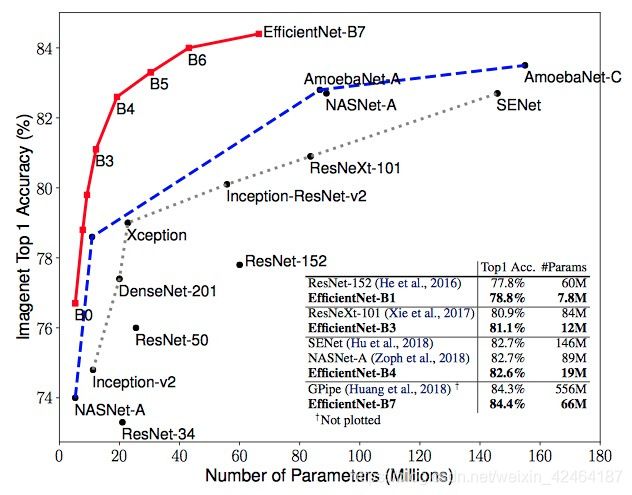
我们证明了我们的增大方法在已有的MobileNets和ResNets上表现很好。尤其是,模型增大的有效性严重依赖于baseline网络;更进一步,我们使用神经网络搜索(Zoph & Le,2017;Tan et al.,2019)开发一个新的baseline网络,并且对它进行扩大得到一个模型家族,叫做EfficientNets。图1总结了在ImageNet上的表现,我们的EfficientNets明显超过其他的ConvNets。尤其是,我们的EfficientNet-B7准确率超过了已有的最好GPipe(Huang et al.,2018),而且少了8.4倍的参数量和减少了6.1倍的前向运算时间。相比于广泛使用的ResNet-50(He et al.,2016),我们的EfficientNet-B4在差不多运算量的情况下将准确率从76.3%提高到了82.6%(+6.3%)。除了ImageNet,EfficientNets的迁移效果也不错,8个数据集中在5个数据集上达到了最高准确率水平,而且比现有的ConvNets减少了21倍的参数量。
相关工作
ConvNet 准确率: 自从AlexNet(Krizhevsky et al.,2012)赢得了2012年ImageNet竞赛的冠军,ConvNets开始通过更大的模型来增加准确率:GoogleNet(Szegedy et al., 2015)赢得了2014年ImageNet的冠军,达到了74.8%的top-1准确率,模型大约6.8M参数量,SENet(Hu et al.,2018)获得了2017年ImageNet的冠军达到了82.7%的top-1准确率使用了145M参数量。最近GPipe(Huang et al.,2018)进一步把ImageNet最好的top-1验证集合的准确率推到了84.3%,使用了557M的参数量:这模型太大了,只有通过把网络分开并将每个部分扩展到不同的加速器,才能使用专门的管道并行库进行训练。而这些模型主要是为了ImageNet设计的,最近的研究表明更好的ImageNet模型在一系列迁移学习的数据集合(Kornblith et al.,2019)以及其他计算机视觉任务比如目标检测(He et al., 2016; Tan et al., 2019).上表现更好,虽然更高的准确率对于许多应用来说是决定性的,但是我们已经碰到了硬件内存的限制,所以进一步提升准确率需要更好的效率。
ConvNet 效率: 深的ConvNets经常参数过量。模型压缩(Han et al., 2016; He et al., 2018; Yang et al., 2018)是一个普遍的方法来降低模型的大小,通过准确率来换取效率。随着移动电话变得普及,手工制作有效率的移动大小的ConvNets也很普遍,比如SqueezeNets (Iandola et al., 2016; Gholami et al., 2018),MobileNets (Howard et al., 2017; Sandler et al., 2018),和 ShuffleNets (Zhang et al., 2018; Ma et al., 2018)。最近神经网络结构搜索在设计高效的移动端大小的ConvNets(Tan et al., 2019; Cai et al., 2019)上越来越流行,通过调节网络的宽度,深度,卷积核的类型和尺寸达到了甚至比手工制作的移动端ConvNets更好的效率。而如何把这些技术应用到更大的模型上是不清楚的,因为更大的模型有更大的设计空间和更昂贵的调节成本。这篇文章的目的是研究超过最高水平准确率的超级大ConvNets的效率。为了达到这个目标,我们继续模型的缩放。
模型缩放: 对于不同的资源限制下,有很多种方式去缩放一个ConvNet:ResNet可以通过调整网络的深度来缩小(e.g., ResNet-18)或放大(e.g., ResNet-200),而WideResNet (Zagoruyko & Komodakis, 2016) 和 MobileNets (Howard et al., 2017)能通过网络的宽度(#channels)来缩放。公认的更大的输入图像尺寸带来更多运算量的同时能够帮助提升准确率。尽管之前的研究(Raghu et al., 2017; Lin & Jegelka, 2018; Sharir & Shashua, 2018; Lu et al., 2018)已经表明了网络的深度和宽度对于ConvNets的表达力都是重要的,但是仍遗留了一个开放性的问题怎样有效的去放缩一个ConvNet来达到更好的效率和准确率呢。我们系统地实验并且经验性的研究了ConvNet全部不到三个维度(网络的宽度,深度和图像分辨率)的缩放。
复合模型缩放
这节我们将公式化缩放问题,研究不同的方法并提出我们新的缩放方法。
问题公式化
一个ConvNet层 i i i可以被定义成一个方程: Y i = F i ( X i ) Y_i=F_i(X_i) Yi=Fi(Xi),其中 F i F_i Fi是运算操作, Y i Y_i Yi是输出的张量, X i X_i Xi是输入的张量维度是 < H i , W i , C i > 1
N = ⨀ i = 1... s F i L i ( X < H i , W i , C i > ) N=\bigodot_{i=1...s}F^{L_i}_i(X_{
其中 F i L i F^{L_i}_i FiLi表示层 F i F_i Fi在第 i i i阶段被重复了 L i L_i Li次, < H i , W i , C i >
不像正常ConvNet的设计主要着眼于发现最好的层结构 F i F_i Fi,模型放大试图在不改变baseline网络预定义的 F i F_i Fi下,扩大网络的长度,宽度及分辨率(H_i, W_i)。通过固定 F i F_i Fi,模型缩放简化了新的资源限制条件下的设计问题,但是仍旧存在一个大的设计空间去探索不同层的 L i L_i Li, C i C_i Ci, H i H_i Hi, W i W_i Wi。为了进一步的减少设计空间,我们限制了所有层必须通过常数比例一致地放缩。我们的目标是在任意给定的资源限制下最大化模型的准确率,可以用公式来表示这个优化问题:
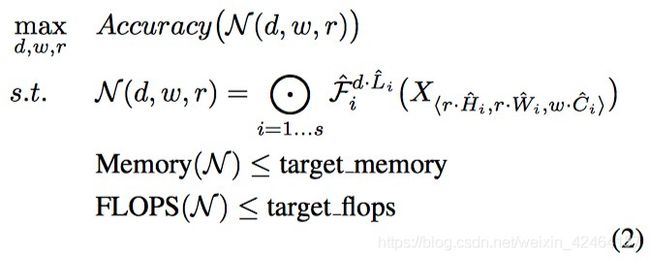
其中 w , d , r w,d,r w,d,r分别是网络的宽度,深度和分辨率的系数; F i ^ , L i ^ , H i ^ , W i ^ , C i ^ \hat{F_i}, \hat{L_i}, \hat{H_i}, \hat{W_i}, \hat{C_i} Fi^,Li^,Hi^,Wi^,Ci^是基础网络预定义的参数(参加表1的例子)。
缩放维度
问题2的主要困难是最优的 d , w , r d,w,r d,w,r彼此依赖并且在不同的资源限制下的值是改变的。由于这个困难,传统的方法大多是对ConvNets的某一个维度进行缩放:
深度(d): 缩放网络的深度是许多ConvNets(He et al., 2016; Huang et al., 2017; Szegedy et al., 2015; 2016).最常用的方法。直观的感觉是越深的ConvNets能捕捉越丰富越复杂的特征,并且在新任务上泛化的很好。然而,由于梯度消失问题(Zagoruyko & Komodakis, 2016)。导致越深的网络也越难训练。尽管几个方法比如跳跃连接(He et al., 2016)和BN(Ioffe & Szegedy, 2015),能够缓解这个训练问题,但在非常深的网络里没有得到准确率的提高:例如,ResNet-1000尽管有更多的层,但和ResNet-101准确率相似。图3(中间)展示了我们的经验研究结果,用不同的系数 d d d来缩放一个baseline模型的深度,进一步证明了对于非常深的ConvNets准确率会衰减。
宽度(w): 缩放网络的宽度普遍用于小模型(Howard et al., 2017; Sandler et al., 2018;Tan et al., 2019).

像文章 (Zagoruyko & Komodakis, 2016)中讨论的那样,更宽的网络能够捕捉更多的细粒度特征并且更容易训练。然而特别宽但很浅的网络很难捕捉到高水平的特征。我们的经验结果在图3左边可以看出,当网络变得越来越宽,那么准确率很快饱和了。
分辨率( r ): 随着输入图像的分辨率越高,ConvNets能够潜在的捕捉更细粒度的图案。从早期的ConvNets的224x224开始,现代ConvNets倾向于使用299x299 (Szegedy et al., 2016)或331x331 (Zoph et al., 2018)的分辨率来得到更好的准确率。最近,GPipe (Huang et al., 2018)达到了ImageNet准确率的最高水平使用480x480的分辨率。更高的分辨率,比如600x600,也被广泛的在目标检测的ConvNets(He et al., 2017; Lin et al., 2017)中使用。图3右边展示了缩放网络分辨率的结果,的确更高的分辨率提高了准确率,但是准确率的增加在非常高的分辨率(r=1.0表示分辨率为224x224并且r=2.5表示分辨率是560x560)时会下降。
观点 1 放大网络宽度,深度或分辨率中任何一个维度都可以提高准确率,但是对于更大的模型准确率的收益减少。
复合缩放
我们经验地发现缩放不同的维度不是独立的。直观来说,对于更大分辨率的图像,我们应该增加网络的深度,这样才能有更大的感受野有助于在包含更多像素的更大的图像中捕捉相似的特征。相应的,当分辨率更高的时候,我们应该也增加网络的宽度,在有更多像素的高分辨率图像中捕捉更多细粒度的图案。这些直觉意味着我们需要配合且平衡不同维度的缩放,而不是传统的单个维度的缩放。
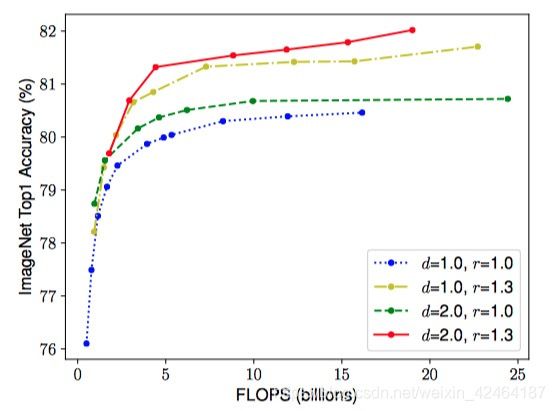
为了验证我们的直觉,我们对比了在不同网络深度和分辨率下缩放宽度的结果,如图4所示。如果我们只是缩放网络宽度w,而不改变深度(d=1.0)和分辨率(r=1.0),准确率就会很快饱和。而在更深(d=2.0)和更高分辨率(r=2.0),缩放网络的宽度在相同的计算量下达到了更好的准确率。这些结果让我们有了第二个观点:
观点 2为了达到更好的准确率和效率,在ConvNet缩放时平衡网络所有宽度,深度和分辨率是起决定作用的。事实上,几个之前的工作(Zoph et al., 2018; Real et al., 2019)已经尝试任意地平衡网络的宽度和深度,但他们都需要冗长乏味的手工调参。
在这篇文章中,我们提出了一个新的复合缩放方法,使用一个复合系数 ϕ \phi ϕ来一致的缩放网络的宽度,深度和分辨率用一个规定的方式:
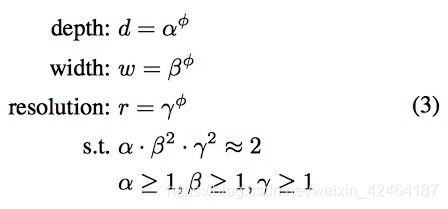
其中 α , β , γ \alpha,\beta,\gamma α,β,γ是通过一个小格子搜索的方法决定的常量。直觉上, ϕ \phi ϕ是一个用户指定的系数来控制有多少的额外资源能够用于模型的缩放,而 α , β , γ \alpha,\beta,\gamma α,β,γ指明了怎么支配这些额外的资源分别到网络的宽度,深度,和分辨率上。尤其是,一个标准卷积操作的运算量的比例是 d , w 2 , r 2 d,w^2,r^2 d,w2,r2,i.e.,双倍的网络深度将带来双倍的运算量,但是双倍的网络宽度或分辨率将会增加运算为4倍。因为卷积操作通常在ConvNets中占据绝大部分计算量,通过3式来缩放ConvNet大约将增加 ( α , β 2 , γ 2 ) (\alpha,\beta^2,\gamma^2) (α,β2,γ2)运算量。本文,我们限制 α ⋅ β 2 ⋅ γ 2 ≈ 2 \alpha \cdot \beta^2 \cdot \gamma^2 \thickapprox 2 α⋅β2⋅γ2≈2所以对于任何新的 ϕ \phi ϕ总共的运算量将大约增加 2 ϕ 2^\phi 2ϕ。
EfficientNet 结构
因为模型缩放不会改变baseline网络的每层操作 F i ^ \hat{F_i} Fi^,有一个好的baseline网络是决定性的。我们将使用已有的ConvNets来评估我们的缩放方法,但是为了更好的证明我们缩放方法的有效性,我们也开发了一个新的移动端大小的baseline,叫做EfficientNet。
受到(Tan et al., 2019)的启发,我们通过利用一个多目标神经网络结构搜索来最优化准确率和运算量。具体地,我们使用和(Tan et al., 2019),相同的搜索空间并且使用 A C C ( m ) ⋅ [ F L O P S ( m ) / T ] w ACC(m) \cdot [FLOPS(m) / T]^w ACC(m)⋅[FLOPS(m)/T]w作为优化目标,其中 A C C ( m ) ACC(m) ACC(m)和 F L O P S ( m ) FLOPS(m) FLOPS(m)表示模型m的准确率和运算量,T是目标运算量,并且w=-0.07是一个控制准确率和运算量平衡的超参数。不像(Tan et al., 2019; Cai et al., 2019),这里我们优化运算量而不是等待时间因为我们没有针对任何具体的硬件设备。我们的研究产生了一个有效的网络,我们叫做EfficientNet-B0。因为我们和(Tan et al., 2019)使用相同的搜索空间,所以这个结构和MnasNet是相似的,除了我们的EfficientNet-B0相对大一点,由于运算量的目标是更大的(我们的运算量目标是400M)。表1展示了EfficientNet-B0的网络结构。主要的构建块是移动倒置瓶颈模块MBConv(Sandler et al., 2018; Tan et al., 2019),我们也增加了squeeze-and-excitation优化(Hu et al., 2018)。
-

从baseline EfficientNet-B0开始,我们应用我们的复合缩放方法用以下两步进行放大:
-
第一步:我们先固定 ϕ = 1 \phi = 1 ϕ=1,假设我们有两倍的可获得资源,并且基于公式2和3来做一个小的格子搜索 α , β , γ \alpha,\beta,\gamma α,β,γ。尤其是我们发现了对于EfficientNet-B0来说最好的值是 α = 1.2 , β = 1.1 , γ = 1.15 \alpha=1.2, \beta=1.1, \gamma=1.15 α=1.2,β=1.1,γ=1.15,在 α ⋅ β 2 ⋅ γ 2 ≈ 2 \alpha \cdot \beta^2 \cdot \gamma^2 \thickapprox 2 α⋅β2⋅γ2≈2限制下。
-
第二步:我们固定 α , β , γ \alpha,\beta,\gamma α,β,γ作为常量,并且使用公式3通过不同的 ϕ \phi ϕ放大baseline网络,获得了Efficient-B1到B7(细节见表2)。
尤其是,通过直接的在一个大模型上搜索 α , β , γ \alpha,\beta,\gamma α,β,γ可能达到更好的效果,但是在更大模型上搜索的代价过分奢侈。我们的方法通过在小的baseline网络上做一次搜索(第一步)解决了这个问题,然后使用了相同的缩放系数得到其他模型(第二步)。

-
实验
这一节,我们将先在已有的ConvNets上评估我们的缩放方法,然后再在我们提出的EfficientNets上进行评估。
放大MobileNets和ResNets
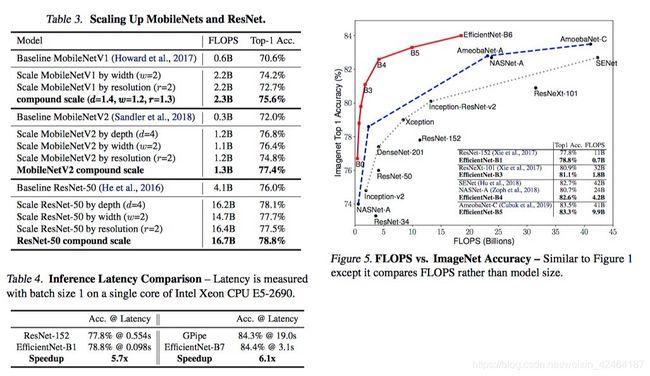
作为一个概念的证明,我们先把我们的缩放方法应用到广泛使用的MobileNets (Howard et al., 2017; Sandler et al., 2018) 和 ResNet (He et al., 2016)上。表3展示了用不同方式缩放他们在ImageNet上的结果。相比于其他单个维度的缩放方法,我们的复合缩放方法在所有的这些模型上提高了准确率,表明了我们提出的缩放方法对于扩展已有ConvNets的有效性。
 -
-

EfficientNet在ImageNet上的结果
我们使用相似于(Tan et al., 2019)的设置在ImageNet上训练我们的EfficientNet:RMSProp优化器的衰减率为0.9,动量为0.9;batch norm动量为0.99;权重衰减率1e-5;初始化学习率为0.256每2.4轮迭代衰减为原来的0.97。我们也使用了swish激活函数(Ramachandran et al., 2018; Elfwing et al., 2018),固定的AutoAugment数据增强策略(Cubuk et al., 2019),和随机的深度(Huang et al., 2016)和drop connect率为0.2。众所周知更大的模型需要更多的正则化,所以我们线性的增加dropout(Srivastava et al., 2014)的比率从EfficientNet-B0的0.2到EfficientNet-B7的0.5。
表2显示了所有从EfficientNet-B0缩放得到的EfficientNet模型的表现。我们的EfficientNet模型通常比相似准确率的ConvNets的参数和运算量少一个量级。尤其是,我们的EfficientNet-B7达到了84.4% top1 / 97.1% top-5的准确率切只用了66M的参数量和37B的FLOPS,比之前最好的GPipe(Huang et al., 2018)有更高的准确率且模型小了8.4倍。图1和图5阐释了代表ConvNets的参数和准确率以及FLOPS和准确率的曲线,其中我们的EfficientNet比其他ConvNets达到了更好的准确率且用更少的参数和FLOPS。尤其是我们的EfficientNet模型不但小而且计算资源占用少。例如我们的EfficientNet-B3比ResNeXt-101(Xie et al., 2017)准确率更高且比之少了18倍的FLOPS。
为了验证计算消耗,我们也度量了几个典型ConvNets在一个实际的CPU上的推理时间,如表4所示,我们给出了20次运算的平均延时时间。我们的EfficientNet-B1比起广泛使用的ResNet-152(He et al., 2016)快了5.7倍,而EfficientNet-B7比GPipe(Huang et al., 2018)快了6.1倍,表明我们的EfficientNets在实际的硬件上的确很快。

-
EfficientNet迁移学习的结果
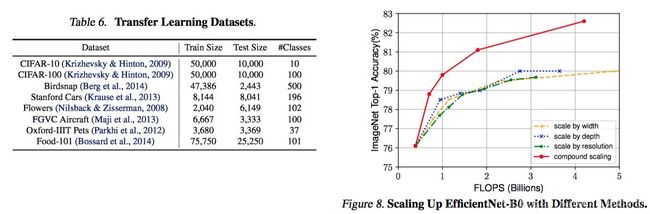
我们也在一系列常用的迁移学习的数据集上评估了我们的EfficientNet,如表6所示。我们借用了与(Kornblith et al., 2019)和(Huang et al., 2018)相同的训练设置,使用ImageNet的预训练模型并且在新数据集上微调。
表5展示了在迁移学习上的效果:(1)相比于公共可获得的模型,比如NASNet-A(Zoph et al., 2018)和Inception-v4(Szegedy et al., 2017)我们的EfficientNet模型达到了更好的准确率且平均4.7倍(最高21倍)的参数减少量。(2)相比于最好的模型,包括DAT(Ngiam et al., 2018)动态合成训练数据和GPipe(Huang et al., 2018)通过特殊的流程并行训练,我们的EfficientNet模型仍旧在5/8的数据集上碾压他们的准确率,而只使用比之小9.6倍的参数量。
图6对比了各种不同模型的准确率-参数的曲线。通常来说,我们的EfficientNets始终比已有的模型,包括(He et al., 2016), DenseNet (Huang et al., 2017), Inception (Szegedy et al., 2017), and NASNet (Zoph et al., 2018)有更好的准确率而且参数少了一个数量级。
讨论
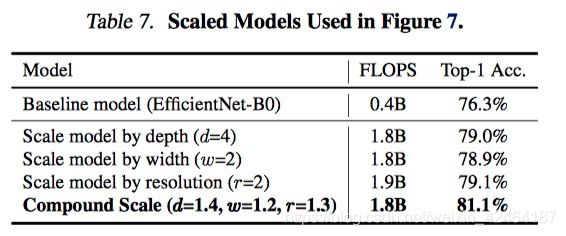
为了理出我们提出的缩放方法在EfficientNet结构上所做的贡献,图8对比了在同样的EfficientNet-B0的baseline网络上使用不同的缩放方法的效果。通常来说,所有的缩放方法都通过损失更多的FLOPS提高了准确率,但是我们的复合缩放方法能够进一步的提高准确率,比其他单个维度的缩放方法,提高了2.5%,表明了我们提出的复合缩放方法的重要性。
为了进一步的理解为什么我们的复合缩放方法能够比其他的方法更好,图7对比了几个用不同的缩放方法得到的有代表性的模型的类别激活映射图的结果。所有的这些模型都缩放自同一个baseline,并且他们的统计信息体现在表7中。图像是随机的从ImageNet的验证集合中挑选的。如图所示,通过复合缩放法得到的模型倾向于更关注相关的区域得到更多的对象细节。而其他的模型或者缺少对象的细节或者不能够捕捉一张图片中的所有对象。
总结
在这篇文章中,我们系统性的研究了ConvNet的缩放并确定了认真平衡网络的宽度,深度和分辨率是重要的,但是一直是缺失的,导致我们不能够得到更好的准确率和效率。为了解决这个问题,我们提出了一个简单且更高效的复合缩放方法,能够让我们很容易地以一种更有原则的方式放大一个baseline ConvNet到任何目标资源限制下,而保持模型的效率。通过这个复合缩放方法的支持,我们证明了一个移动尺寸的模型EfficientNet模型能被非常有效的放大,在少一个量级的参数和FLOPS下超过目前最高的准确率,在包括ImageNet数据集在内的常用的5个迁移学习的数据集。
参考
Berg, T., Liu, J., Woo Lee, S., Alexander, M. L., Jacobs, D. W., and Belhumeur, P. N. Birdsnap: Large-scale fine-grained visual categorization of birds. CVPR, pp. 2011–2018, 2014.
Bossard, L., Guillaumin, M., and Van Gool, L. Food-101mining discriminative components with random forests. ECCV, pp. 446–461, 2014.
Cai, H., Zhu, L., and Han, S. Proxylessnas: Direct neural architecture search on target task and hardware. ICLR, 2019.
Chollet, F. Xception: Deep learning with depthwise separable convolutions. CVPR, pp. 1610–02357, 2017.
Cubuk, E. D., Zoph, B., Mane, D., Vasudevan, V., and Le, Q. V. Autoaugment: Learning augmentation policies from data. CVPR, 2019.
Elfwing, S., Uchibe, E., and Doya, K. Sigmoid-weighted linear units for neural network function approximation in reinforcement learning. Neural Networks, 107:3–11, 2018.
Gholami, A., Kwon, K., Wu, B., Tai, Z., Yue, X., Jin, P., Zhao, S., and Keutzer, K. Squeezenext: Hardware-aware neural network design. ECV Workshop at CVPR’18, 2018.
Han, S., Mao, H., and Dally, W. J. Deep compression:
Compressing deep neural networks with pruning, trained quantization and huffman coding. ICLR, 2016.
He, K., Zhang, X., Ren, S., and Sun, J. Deep residual learning for image recognition. CVPR, pp. 770–778, 2016.
He, K., Gkioxari, G., Doll´ar, P., and Girshick, R. Mask r-cnn. ICCV, pp. 2980–2988, 2017.
He, Y., Lin, J., Liu, Z., Wang, H., Li, L.-J., and Han, S.
Amc: Automl for model compression and acceleration on mobile devices. ECCV, 2018.
Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D., Wang, W., Weyand, T., Andreetto, M., and Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv preprint arXiv:1704.04861, 2017.
Hu, J., Shen, L., and Sun, G. Squeeze-and-excitation networks. CVPR, 2018.
Huang, G., Sun, Y., Liu, Z., Sedra, D., and Weinberger, K. Q. Deep networks with stochastic depth. ECCV, pp. 646–661, 2016.
Huang, G., Liu, Z., Van Der Maaten, L., and Weinberger, K. Q. Densely connected convolutional networks. CVPR, 2017.
Huang, Y., Cheng, Y., Chen, D., Lee, H., Ngiam, J., Le, Q. V., and Chen, Z. Gpipe: Efficient training of giant neural networks using pipeline parallelism. arXiv preprint arXiv:1808.07233, 2018.
Iandola, F. N., Han, S., Moskewicz, M. W., Ashraf, K., Dally, W. J., and Keutzer, K. Squeezenet: Alexnet-level accuracy with 50x fewer parameters and <0.5 mb model size. arXiv preprint arXiv:1602.07360, 2016.
Ioffe, S. and Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. ICML, pp. 448–456, 2015.
Kornblith, S., Shlens, J., and Le, Q. V. Do better imagenet models transfer better? CVPR, 2019.
Krause, J., Deng, J., Stark, M., and Fei-Fei, L. Collecting a large-scale dataset of fine-grained cars. Second Workshop on Fine-Grained Visual Categorizatio, 2013.
Krizhevsky, A. and Hinton, G. Learning multiple layers of features from tiny images. Technical Report, 2009.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. Imagenet classification with deep convolutional neural networks. In NIPS, pp. 1097–1105, 2012.
Lin, H. and Jegelka, S. Resnet with one-neuron hidden layers is a universal approximator. NeurIPS, pp. 61726181, 2018.
Lin, T.-Y., Doll´ar, P., Girshick, R., He, K., Hariharan, B., and Belongie, S. Feature pyramid networks for object detection. CVPR, 2017.
Liu, C., Zoph, B., Shlens, J., Hua, W., Li, L.-J., Fei-Fei, L., Yuille, A., Huang, J., and Murphy, K. Progressive neural architecture search. ECCV, 2018.
Lu, Z., Pu, H., Wang, F., Hu, Z., and Wang, L. The expressive power of neural networks: A view from the width. NeurIPS, 2018.
Ma, N., Zhang, X., Zheng, H.-T., and Sun, J. Shufflenet v2:
Practical guidelines for efficient cnn architecture design. ECCV, 2018.
Mahajan, D., Girshick, R., Ramanathan, V., He, K., Paluri, M., Li, Y., Bharambe, A., and van der Maaten, L. Exploring the limits of weakly supervised pretraining. arXiv preprint arXiv:1805.00932, 2018.
Maji, S., Rahtu, E., Kannala, J., Blaschko, M., and Vedaldi, A. Fine-grained visual classification of aircraft. arXiv preprint arXiv:1306.5151, 2013.
Ngiam, J., Peng, D., Vasudevan, V., Kornblith, S., Le, Q. V., and Pang, R. Domain adaptive transfer learning with specialist models. arXiv preprint arXiv:1811.07056, 2018.
Nilsback, M.-E. and Zisserman, A. Automated flower classification over a large number of classes. ICVGIP, pp. 722–729, 2008.
Parkhi, O. M., Vedaldi, A., Zisserman, A., and Jawahar, C.
Cats and dogs. CVPR, pp. 3498–3505, 2012.
Raghu, M., Poole, B., Kleinberg, J., Ganguli, S., and SohlDickstein, J. On the expressive power of deep neural networks. ICML, 2017.
Ramachandran, P., Zoph, B., and Le, Q. V. Searching for activation functions. arXiv preprint arXiv:1710.05941, 2018.
Real, E., Aggarwal, A., Huang, Y., and Le, Q. V. Regularized evolution for image classifier architecture search. AAAI, 2019.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bernstein, M., et al. Imagenet large scale visual recognition challenge. International Journal of Computer Vision, 115(3): 211–252, 2015.
Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., and Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. CVPR, 2018.
Sharir, O. and Shashua, A. On the expressive power of overlapping architectures of deep learning. ICLR, 2018.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1):1929–1958, 2014.
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V., and Rabinovich, A. Going deeper with convolutions. CVPR, pp. 1–9, 2015.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna, Z. Rethinking the inception architecture for computer vision. CVPR, pp. 2818–2826, 2016.
Szegedy, C., Ioffe, S., Vanhoucke, V., and Alemi, A. A.
Inception-v4, inception-resnet and the impact of residual connections on learning. AAAI, 4:12, 2017.
Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandler, M., Howard, A., and Le, Q. V. MnasNet: Platform-aware neural architecture search for mobile. CVPR, 2019.
Xie, S., Girshick, R., Doll´ar, P., Tu, Z., and He, K. Aggregated residual transformations for deep neural networks. CVPR, pp. 5987–5995, 2017.
Yang, T.-J., Howard, A., Chen, B., Zhang, X., Go, A., Sze, V., and Adam, H. Netadapt: Platform-aware neural network adaptation for mobile applications. ECCV, 2018.
Zagoruyko, S. and Komodakis, N. Wide residual networks.
BMVC, 2016.
Zhang, X., Li, Z., Loy, C. C., and Lin, D. Polynet: A pursuit of structural diversity in very deep networks. CVPR, pp. 3900–3908, 2017.
Zhang, X., Zhou, X., Lin, M., and Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. CVPR, 2018.
Zhou, B., Khosla, A., Lapedriza, A., Oliva, A., and Torralba, A. Learning deep features for discriminative localization. CVPR, pp. 2921–2929, 2016.
Zoph, B. and Le, Q. V. Neural architecture search with reinforcement learning. ICLR, 2017.
Zoph, B., Vasudevan, V., Shlens, J., and Le, Q. V. Learning transferable architectures for scalable image recognition. CVPR, 2018.