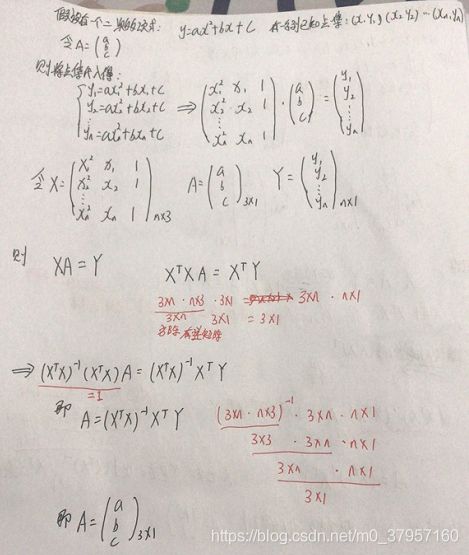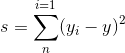PCL：拟合平面直线和曲线以及空间曲线的原理到算法实现

使用两种思路进行直线拟合：

1.利用逆矩阵思想

--------------进行下列公式的推导需要理解逆矩阵（求A矩阵的逆矩阵，则A矩阵必须是方阵）的知识：

（1）为什么要引入逆矩阵呢？

逆矩阵可以类比成数字的倒数，比如数字5的倒数是1/5，矩阵A的“倒数”是A的逆矩阵。5*(1/5)=1, A*（A的逆矩阵） = I，I是单位矩阵。引入逆矩阵的原因之一是用来实现矩阵的除法。比如有矩阵X，A，B，其中X*A = B，我们要求X矩阵的值。本能来说，我们只需要将B/A就可以得到X矩阵了。但是对于矩阵来说，不存在直接相除的概念。我们需要借助逆矩阵，间接实现矩阵的除法。具体的做法是等式两边在相同位置同时乘以矩阵A的逆矩阵，如下所示，X*A*（A的逆矩阵）= B*（A的逆矩阵）。由于A*（A的逆矩阵） = I，即单位矩阵，任何矩阵乘以单位矩阵的结果都是其本身。所以，我们可以得到X =  B*（A的逆矩阵）。

（2）什么是逆矩阵？

设A是数域上的一个n阶方阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=E。 则我们称B是A的逆矩阵，而A则被称为可逆矩阵。E为n阶单位矩阵。

（3）逆矩阵有哪些性质？

（4）如何计算一个n阶方阵的逆矩阵？

https://www.sohu.com/a/226465524_224832

首先利用逆矩阵思想来进行平面直线的推导过程如下：

   

平面中的多项式表示平面中的曲线：（曲线系数推导过程如上右图）

以下是详细代码展示：（后边代码没有注释啊啊，因为后边有的我也不是很明白）

//头文件
#pragma once
//fitting.h
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
using namespace pcl;
using namespace Eigen;
typedef PointXYZ PointT;

class fitting
{
public:
	fitting();//构造函数
	~fitting();//析构函数
	//以下都是声明函数即类的成员函数
	void setinputcloud(PointCloud::Ptr input_cloud);//点云输入
	//投影至XOY，规则格网，求每个格网内点云坐标均值
	void grid_mean_xyz(double x_resolution, double y_resolution, vector&x_mean, vector &y_mean, vector&z_mean, PointCloud::Ptr &new_cloud);//投影至XOY，规则格网，求每个格网内点云坐标均值
	void grid_mean_xyz_display(PointCloud::Ptr new_cloud);//均值结果三维展示
	void line_fitting(vectorx, vectory, double &k, double &b);//y=kx+b//平面直线
	void polynomial2D_fitting(vectorx, vectory, double &a, double &b, double &c);//y=a*x^2+b*x+c;//平面曲线
	void polynomial3D_fitting(vectorx, vectory, vectorz, double &a, double &b, double &c);//z=a*(x^2+y^2)+b*sqrt(x^2+y^2)+c//空间曲线
	void polynomial3D_fitting_display(double step_);//三维曲线展示
	void display_point(vectorvector_1, vectorvector_2);//散点图显示
	void display_line(vectorvector_1, vectorvector_2, double c, double b, double a = 0);//拟合的平面直线或曲线展示
private://类的私有成员通过成员函数进行访问
	PointCloud::Ptr cloud;
	PointT point_min;
	PointT point_max;
	double a_3d;
	double b_3d;
	double c_3d;
	double k_line;
	double b_line;
};

//源文件fitting.cpp
#include "fitting.h"
fitting::fitting()//构造函数
{
}
fitting::~fitting()//析构函数
{
	cloud->clear();
}
//定义点云输入函数
void fitting::setinputcloud(PointCloud::Ptr input_cloud) 
{
	cloud = input_cloud;
	getMinMax3D(*input_cloud, point_min, point_max);//getMinMax3D该函数输入点云数据，将所有xyz中最小的值和xyz中最大的值输出到pcl::PointXYZ中，即pcl::PointXYZ min_p, max_p;
}
//将点云数据投影至XOY，并划分为规则格网，求每个格网内点云坐标均值
void fitting::grid_mean_xyz(double x_resolution, double y_resolution, vector&x_mean, vector &y_mean, vector&z_mean, PointCloud::Ptr &new_cloud) 
{
	if (y_resolution <= 0)//表示如果输入的分辨率小于0，则不进行Y方向的分段处理
	{
		y_resolution = point_max.y - point_min.y;//输入的分辨率小于0则Y方向的分辨率重新调整为Y值的最大值与最小值之差
	}
	int raster_rows, raster_cols;//定义行数row和列数col
	raster_rows = ceil((point_max.x - point_min.x) / x_resolution);//ceil() 函数向上舍入为最接近的整数。如需向下舍入为最接近的整数，请查看 floor(),函数floor(123.5)返回123。如需对浮点数进行四舍五入，请查看 round() 函数。
	raster_cols = ceil((point_max.y - point_min.y) / y_resolution);// ceil(123.5)返回大于或者等于指定表达式的最小整数，返回124
	//容器都是类模板，是一种可变长数组。它们实例化后就成为容器类。用容器类定义的对象称为容器对象。
	//vector 是顺序容器的一种。vector 是可变长的动态数组
	vectoridx_point;//idx_point就是容器对象//点的索引
	vector>>row_col;//row_col是一个三重数组，第一重是实际行号（就是有点的）（因为上述划分的raster_rows是总行数有可能有的行列里边没有投影进去点），第二重是实际列号第三重是该行列中的点坐标及索引即（行，列，XYZ索引）
	vector>col_;//col_是一个二重数组，表示上述三重数组中第二重存放的是列
	vectorvector_4;//vector_4是个一重数组，存放的是点坐标及索引
	vector_4.resize(4);//将vector_4的现有元素个数调整至4个，多则删，少则补，其值随机
	col_.resize(raster_cols, vector_4);//将col_的现有元素个数调整至raster_cols个，多则删，少则补，其值为col_（因为raster_cols是划分定义的行数）
	row_col.resize(raster_rows, col_);//将row_col的现有元素个数调整至raster_rows个，多则删，少则补，其值为col_
	int point_num = cloud->size();
	//填充三重数组
	for (int i_point = 0; i_point < point_num; i_point++)
	{
		//找到当前点所在的(行)(列)
		int row_idx = ceil((cloud->points[i_point].x - point_min.x) / x_resolution) - 1;//该点当前所在的行（有可能很多个点算出来都在这个行内比如都是3.3就取第三行）
		int col_idx = ceil((cloud->points[i_point].y - point_min.y) / y_resolution) - 1;//计算当前Y值被划分到了哪个列
		if (row_idx < 0)
			row_idx = 0;//如果行列都小于0,则将row_idx赋值为0；（此处不存在因为减去的就是最小值不可能为负）
		if (col_idx < 0)
			col_idx = 0;
		//找到了行列后把(xyz索引)塞进去
		row_col[row_idx][col_idx][0] += cloud->points[i_point].x;//把落尽该格子内的所有点的所有x值相加，为了下边求格网的平均值
		row_col[row_idx][col_idx][1] += cloud->points[i_point].y;//把点云坐标的所有y值相加
		row_col[row_idx][col_idx][2] += cloud->points[i_point].z;//把点云坐标的所有z值相加
		row_col[row_idx][col_idx][3] += 1;//落到该网格的总的点数就是一共有多少个点落到目前这个网格子
	}
	PointT point_mean_tem;
	//求每个网格的平均值
	for (int i_row = 0; i_row < row_col.size(); i_row++)
	{
		for (int i_col = 0; i_col < row_col[i_row].size(); i_col++)
		{
			if (row_col[i_row][i_col][3] != 0)//不等于0就表明
			{
				double x_mean_tem = row_col[i_row][i_col][0] / row_col[i_row][i_col][3];//求x的平均（该网格内点的x总和除以点的总个数）
				double y_mean_tem = row_col[i_row][i_col][1] / row_col[i_row][i_col][3];//求y的平均
				double z_mean_tem = row_col[i_row][i_col][2] / row_col[i_row][i_col][3];//求z的平均
				x_mean.push_back(x_mean_tem);
				y_mean.push_back(y_mean_tem);
				z_mean.push_back(z_mean_tem);
				point_mean_tem.x = x_mean_tem;
				point_mean_tem.y = y_mean_tem;
				point_mean_tem.z = z_mean_tem;
				new_cloud->push_back(point_mean_tem);//将他们的平均值保存在新的点云中
			}
		}
	}
}
//每个格网内点云坐标均值结果三维展示
void fitting::grid_mean_xyz_display(PointCloud::Ptr new_cloud) {
	visualization::PCLVisualizer::Ptr view(new visualization::PCLVisualizer("分段质心拟合"));//可视化界面标题
	//pcl::visualization::PointCloudColorHandlerCustom sources_cloud_color(source,250,0,0); //这句话的意思是：对输入为pcl::PointXYZ类型的点云，着色为红色。其中，source表示真正处理的点云，sources_cloud_color表示处理结果.
	visualization::PointCloudColorHandlerCustomcolor_1(new_cloud, 255, 0, 0);//创建一个自定义颜色处理器PointCloudColorHandlerCustom对象，给点云着色并设置颜色为红色
	//view->addPointCloud(source,sources_cloud_color,"sources_cloud_v1",v1); //将点云source,处理结果sources_cloud_color,添加到视图中，其中,双引号中的sources_cloud_v1,表示该点云的”标签“，我们依然可以称之为”名字“，之所以设置各个处理点云的名字，是为了在后续处理中易于区分; v1表是添加到哪个视图窗口（pcl中可设置多窗口模式）
	view->addPointCloud(new_cloud, color_1, "11");//加载点云
	//view->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE,3,"sources_cloud_v1"); //设置点云属性. 其中PCL_VISUALIZER_POINT_SIZE表示设置点的大小为3,双引号中”sources_cloud_v1“,就是步骤2中所说的标签。
	//view->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_OPACITY,1,"sources_cloud_v1"); //主要用来设置标签点云的不透明度，表示对标签名字为"sources_cloud_v1"的标签点云设置不透明度为1,也就是说透明度为0. 默认情况下完全不透明。
	view->setPointCloudRenderingProperties(visualization::PCL_VISUALIZER_POINT_SIZE, 3, "11");
	PointCloud::Ptr new_cloud_final(new PointCloud);//创建一个新的点云用于存储结果
	for (int i_point = 0; i_point < cloud->size(); i_point++)
	{
		PointT tem_point;
		tem_point.x = cloud->points[i_point].x;
		tem_point.y = cloud->points[i_point].y;
		tem_point.z = cloud->points[i_point].z;
		new_cloud_final->push_back(tem_point);
	}
	view->addPointCloud(new_cloud_final, "22");
	view->spin();
}
//拟合平面直线y=kx+b
//引用的本质：在定义或声明函数时，我们可以将函数的形参指定为引用的形式，这样在调用函数时就会将实参和形参绑定在一起，让它们都指代同一份数据。如此一来，如果在函数体中修改了形参的数据，那么实参的数据也会被修改，从而拥有“在函数内部影响函数外部数据”的效果。
void fitting::line_fitting(vectorx, vectory, double &k, double &b) //此函数输入是x,y；输出是k,b；是C++中的引用知识（“在函数内部影响函数外部数据”）
{
	MatrixXd A_(2, 2), B_(2, 1), A12(2, 1);//A_是个矩阵两行两列，其他同理
	int num_point = x.size();//num_point等于输入的x的总个数
	double A01(0.0), A02(0.0), B00(0.0), B10(0.0);//A01表示第0行第1列//A01(0.0), A02(0.0)表明A矩阵的第一行都初始化为0
	for (int i_point = 0; i_point < num_point; i_point++)
	{
		A01 += x[i_point] * x[i_point];
		A02 += x[i_point];
		B00 += x[i_point] * y[i_point];
		B10 += y[i_point];
	}
	A_ << A01, A02,
		A02, num_point;//把这四个数塞给A矩阵；A矩阵就是推导中的x转置乘x的逆
	B_ << B00,
		B10;//B矩阵就是X转置乘Y
	A12 = A_.inverse()*B_;//A_.inverse()是求A的逆矩阵；
	k = A12(0, 0);//A12是两行一列，那么k就是第0行第0列
	b = A12(1, 0);//b就是第1行第0列
}
//拟合y=a*x^2+b*x+c;//平面曲线
void fitting::polynomial2D_fitting(vectorx, vectory, double &a, double &b, double &c) {
	MatrixXd A_(3, 3), B_(3, 1), A123(3, 1);
	int num_point = x.size();
	double A01(0.0), A02(0.0), A12(0.0), A22(0.0), B00(0.0), B10(0.0), B12(0.0);
	for (int i_point = 0; i_point < num_point; i_point++)
	{
		A01 += x[i_point];
		A02 += x[i_point] * x[i_point];
		A12 += x[i_point] * x[i_point] * x[i_point];
		A22 += x[i_point] * x[i_point] * x[i_point] * x[i_point];
		B00 += y[i_point];
		B10 += x[i_point] * y[i_point];
		B12 += x[i_point] * x[i_point] * y[i_point];
	}
	A_ << num_point, A01, A02,
		A01, A02, A12,
		A02, A12, A22;
	B_ << B00,
		B10,
		B12;
	A123 = A_.inverse()*B_;
	a = A123(2, 0);
	b = A123(1, 0);
	c = A123(0, 0);
}
//拟合空间曲线
void fitting::polynomial3D_fitting(vectorx, vectory, vectorz, double &a, double &b, double &c) 
{
	int num_point = x.size();
	MatrixXd A_(3, 3), B_(3, 1), A123(3, 1);
	double A01(0.0), A02(0.0), A12(0.0), A22(0.0), B00(0.0), B10(0.0), B12(0.0);
	for (int i_point = 0; i_point < num_point; i_point++)
	{
		double x_y = sqrt(pow(x[i_point], 2) + pow(y[i_point], 2));
		A01 += x_y;
		A02 += pow(x_y, 2);
		A12 += pow(x_y, 3);
		A22 += pow(x_y, 4);
		B00 += z[i_point];
		B10 += x_y * z[i_point];
		B12 += pow(x_y, 2) * z[i_point];
	}
	A_ << num_point, A01, A02,
		A01, A02, A12,
		A02, A12, A22;
	B_ << B00,
		B10,
		B12;
	A123 = A_.inverse()*B_;
	line_fitting(x, y, k_line, b_line);
	a = A123(2, 0);
	b = A123(1, 0);
	c = A123(0, 0);
	c_3d = c;
	b_3d = b;
	a_3d = a;
}
//空间曲线展示
void fitting::polynomial3D_fitting_display(double step_) //传入的参数相当于步长
{
	PointT point_min_, point_max_;
	getMinMax3D(*cloud, point_min_, point_max_);
	//利用最小外包框的x值，向拟合的直线做垂足，垂足的交点即为三维曲线的端点值***********
	int idx_minx, idx_maxy;//x取到最大值和最小值的点号索引
	for (int i_point = 0; i_point < cloud->size(); i_point++)
	{
		if (cloud->points[i_point].x == point_min_.x) 
			idx_minx = i_point;
		if (cloud->points[i_point].x == point_max_.x) 
			idx_maxy = i_point;
	}
	float m_min = cloud->points[idx_minx].x + k_line*cloud->points[idx_minx].y;
	float m_max = cloud->points[idx_maxy].x + k_line*cloud->points[idx_maxy].y;

	float x_min = (m_min - b_line*k_line) / (1 + k_line*k_line);
	float x_max = (m_max - b_line*k_line) / (1 + k_line*k_line);
	//---------------------------------------------------------------------------------------
	vectorxx, yy, zz;
	int step_num = ceil((x_max - x_min) / step_);
	vtkSmartPointer points = vtkSmartPointer::New();
	for (int i_ = 0; i_ < step_num + 1; i_++)
	{
		double tem_value = x_min + i_*step_;
		if (tem_value>x_max)
		{
			tem_value = x_max;
		}
		xx.push_back(tem_value);
		yy.push_back(k_line*xx[i_] + b_line);
		double xxyy = sqrt(pow(xx[i_], 2) + pow(yy[i_], 2));
		zz.push_back(c_3d + b_3d*xxyy + a_3d*pow(xxyy, 2));
		points->InsertNextPoint(xx[i_], yy[i_], zz[i_]);
	}
	vtkSmartPointer polyLine = vtkSmartPointer::New();
	vtkSmartPointer polyData = vtkSmartPointer::New();
	vtkSmartPointer cells = vtkSmartPointer::New();
	polyData->SetPoints(points);
	polyLine->GetPointIds()->SetNumberOfIds(points->GetNumberOfPoints());
	for (unsigned int i = 0; i < points->GetNumberOfPoints(); i++)
		polyLine->GetPointIds()->SetId(i, i);
	cells->InsertNextCell(polyLine);
	polyData->SetLines(cells);
	visualization::PCLVisualizer::Ptr viewer(new visualization::PCLVisualizer("最后拟合的多项式曲线"));
	viewer->addModelFromPolyData(polyData, "1");
	//*******************************************
	PointCloud::Ptr tem_point(new PointCloud);
	for (int i = 0; i < xx.size(); i++)
	{
		PointT point_;
		point_.x = xx[i];
		point_.y = yy[i];
		point_.z = zz[i];
		tem_point->push_back(point_);
	}
	visualization::PointCloudColorHandlerCustomcolor1(tem_point, 255, 0, 0);
	viewer->addPointCloud(tem_point, color1, "point1");
	viewer->setPointCloudRenderingProperties(visualization::PCL_VISUALIZER_POINT_SIZE, 3, "point1");

	PointCloud::Ptr tem_point1(new PointCloud);
	for (int i = 0; i < cloud->size(); i++)
	{
		PointT point_1;
		point_1.x = cloud->points[i].x;
		point_1.y = cloud->points[i].y;
		point_1.z = cloud->points[i].z;
		tem_point1->push_back(point_1);
	}
	viewer->addPointCloud(tem_point1, "orginal");
	viewer->setPointCloudRenderingProperties(visualization::PCL_VISUALIZER_POINT_SIZE, 2, "orginal");
	//显示端点
	PointCloud::Ptr duandian_point(new PointCloud);
	duandian_point->push_back(tem_point->points[0]);
	duandian_point->push_back(tem_point->points[tem_point->size() - 1]);
	visualization::PointCloudColorHandlerCustomcolor2(duandian_point, 0, 255, 255);
	viewer->addPointCloud(duandian_point, color2, "duandian");
	viewer->setPointCloudRenderingProperties(visualization::PCL_VISUALIZER_POINT_SIZE, 5, "duandian");
	cout << "端点值1为：" << "X1= " << duandian_point->points[0].x << ", " << "Y1= " << duandian_point->points[0].y << ", " << "Z1= " << duandian_point->points[0].z << endl;
	cout << "端点值2为：" << "X2= " << duandian_point->points[1].x << ", " << "Y2= " << duandian_point->points[1].y << ", " << "Z2= " << duandian_point->points[1].z << endl;
	cout << "空间多项式曲线方程为： " << "z=" << a_3d << "*(x^2+y^2)+" << b_3d << "*sqrt(x^2+y^2)+" << c_3d << endl;
	viewer->spin();
	//拟合曲线+端点值+散点图二维平面展示，有需要可以取消注释----------------------------------------------------------
	/*vectorvector_1, vector_2, vector_3, vector_4;
	vector_1.push_back(duandian_point->points[0].x);
	vector_1.push_back(duandian_point->points[1].x);
	vector_2.push_back(duandian_point->points[0].y);
	vector_2.push_back(duandian_point->points[1].y);
	for (int i = 0; i < cloud->size();i++)
	{
	vector_3.push_back(cloud->points[i].x);
	vector_4.push_back(cloud->points[i].y);
	}
	std::vector func1(2, 0);
	func1[0] = b_line;
	func1[1] = k_line;
	visualization::PCLPlotter *plot_line1(new visualization::PCLPlotter);
	plot_line1->addPlotData(func1, vector_1[0], vector_1[1]);
	plot_line1->addPlotData(vector_3, vector_4, "display", vtkChart::POINTS);//X,Y均为double型的向量
	plot_line1->addPlotData(vector_1, vector_2, "display", vtkChart::POINTS);//X,Y均为double型的向量
	plot_line1->setShowLegend(false);
	plot_line1->plot();*/
}
void fitting::display_point(vectorvector_1, vectorvector_2) {
	visualization::PCLPlotter *plot_line1(new visualization::PCLPlotter);
	plot_line1->addPlotData(vector_1, vector_2, "display", vtkChart::POINTS);//X,Y均为double型的向量
	plot_line1->setShowLegend(false);
	plot_line1->plot();
}
void fitting::display_line(vectorvector_1, vectorvector_2, double c, double b, double a) {
	visualization::PCLPlotter *plot_line1(new visualization::PCLPlotter);
	std::vector func1(3, 0);
	func1[0] = c;
	func1[1] = b;
	func1[2] = a;
	plot_line1->addPlotData(func1, point_min.x, point_max.x);
	plot_line1->addPlotData(vector_1, vector_2, "display", vtkChart::POINTS);//X,Y均为double型的向量
	plot_line1->setShowLegend(false);
	plot_line1->plot();
}

//主函数
#include 
#include "fitting.h"
using namespace std;
using namespace pcl;
using namespace Eigen;//Eigen是可以用来进行线性代数、矩阵、向量操作等运算的C++库

typedef PointXYZ PointT;

int main() {
	PointCloud::Ptr cloud(new PointCloud);
	string ss("C:\\Users\\admin\\Desktop\\TEST22.pcd");
	io::loadPCDFile(ss, *cloud);

	vectorX, Y, Z;
	for (int i_point = 0; i_point < cloud->size(); i_point++)
	{
		X.push_back(cloud->points[i_point].x);//大X是原始点云的所有x集合
		Y.push_back(cloud->points[i_point].y);
		Z.push_back(cloud->points[i_point].z);
	}
	vectorx_mean, y_mean, z_mean;
	PointCloud::Ptr point_mean(new PointCloud);
	double a, b, c, k_line, b_line;//所有的函数中传出的参数
	fitting fit_;
	fit_.setinputcloud(cloud);//点云输入
	fit_.line_fitting(X, Y, k_line, b_line);//直线拟合X,Y是传入参数；k_line, b_line是传出参数（C++中的引用知识）
	fit_.display_line(X, Y, b_line, k_line);//显示拟合的直线，必须先输入常量
	fit_.polynomial2D_fitting(X, Z, a, b, c);
	fit_.display_line(X, Z, c, b, a);//显示拟合的平面多项式曲线，输入顺序为 常量，一阶系数，二阶系数
	fit_.grid_mean_xyz(0.5, -1, x_mean, y_mean, z_mean, point_mean);//0.5表示x方向的步长，-1(小于0就行)表示y方向不分段，如需分段，则设置相应步长
	fit_.grid_mean_xyz_display(point_mean);//展示均值结果
	fit_.display_point(X, Y);//显示散点
	fit_.display_point(x_mean, y_mean);//显示均值散点
	fit_.polynomial3D_fitting(x_mean, y_mean, z_mean, a, b, c);//用分段质心的均值去拟合3维曲线
    //fit_.polynomial3D_fitting(X, Y, Z, a, b, c);//直接拟合
	fit_.polynomial3D_fitting_display(0.5);//三维曲线展示

	return 0;
}

2.使用最小二乘原理

PS：首先对于最小二乘思想大家应该掌握，最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

最小二乘法（英文：least square method)是一种常用的数学优化方法，所谓二乘就是平方的意思。这平方一词指的是在拟合一个函数的时候，通过最小化误差的平方来确定最佳的匹配函数，所以最小二乘、最小平方指的就是拟合的误差平方达到最小。

以直线拟合为例，已知有一组平面上的点集。基于这些点拟合一条直线，设直线方程为:

                                                               

那么那么算法的输入就是这些点集，需要求取的为直线方程的参数a,b。

（1）平方偏差之和为:

                                                       

                                                            

那么，以上公式已知的是xi,yi, 未知且要求取的是a、b。不同的a、b会得到不同的S，求取的是在S最小的时候求取a、b。这是一个二元a,b函数,此问题实际上就是多元函数的极值与最值问题，要求解函数极值时二元变量数值，这里要用到二元函数取极值的必要条件：

     

部分代码：

void mv::LineFit::FitLineByRegression()
{
    // 设置权重 | weights setting
    _weigths = std::vector(_points.size(), 1);
    // AX = B
    // 构造A矩阵 | Construct A mat
    const int N = 2;
    cv::Mat A = cv::Mat::zeros(N, N, CV_64FC1);

    for (int row = 0;row < A.rows;row++)
    {
        for (int col = 0; col < A.cols;col++)
        {
            for (int k = 0;k < _points.size();k++)
            {
                A.at(row, col) = A.at(row, col) + pow(_points[k].x, row + col) * _weigths[k];
            }
        }
    }
    //构造B矩阵 | Construct B mat
    cv::Mat B = cv::Mat::zeros(N, 1, CV_64FC1);
    for (int row = 0;row < B.rows;row++)
    {
        for (int k = 0;k < _points.size();k++)
        {
            B.at(row, 0) = B.at(row, 0) + pow(_points[k].x, row)*_points[k].y * _weigths[k];
        }
    }
    // 求解A*X = B | Solve the A*X = B
    cv::Mat X;
    cv::solve(A, B, X,cv::DECOMP_LU);
    // y = b + ax
    _result.b = X.at(0,0);
    _result.a = X.at(1, 0);
}//FitLineByRegression

完整代码链接：https://github.com/mangosroom/machine-vision-algorithms-library/tree/master/src/linefit

参照博客：https://mangoroom.cn/opencv/least-square-method-line-fit.html