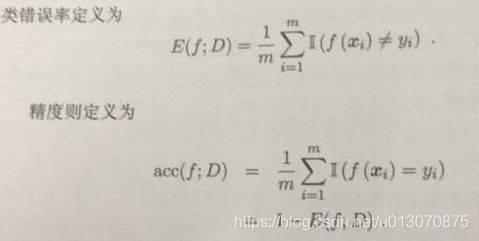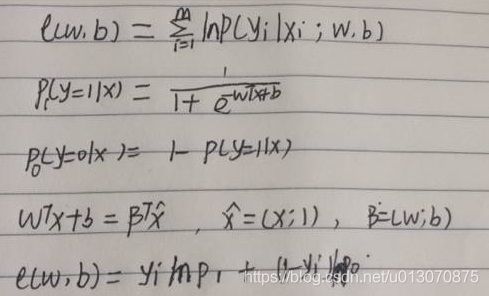机器学习-周志华总结
机器学习知识图谱:
![]()
学习机器学习前了解问题:
机器学习中很多算法,都需要深刻理解,做到能够口述推导过程、或手动推导的程度。
1. 定义机器学习需要解决的问题类型。
2.机器学习模型的含义:
3.构建和应用一个机器学习算法的基本流程
4.分析机器学习的优势和劣势。
机器学习要解决的问题分为两类回归和分类。
机器学习算法,就是机器学习模型。机器学习算法和非机器学习算法的区别是在无人类干扰的情况下,该模型能够自己学习来改变自己,从而保证输入与输出结果的一致。
机器学习算法定义:一个函数F,根据输入,确定输出。只是该函数不是预先定义好与固定的函数,而是需要从历史数据中学习得到的函数。数据不同,模型也就不一样。
机器学习的任务:从假设空间中,学习该函数。找到输入与输出之间的关系。
有监督和无监督区别与含义:
当给出一个机器学习的问题时,就可以判断它是否是一个有监督问题还是无监督问题。有监督学习是由数据是否含有标签决定的。
机器学习算法的流程是:
1.确定机器学习的问题,分类或回归。
2.确定学习模型也就是算法结构,网络结构,可根据有无监督进行分类,当然两者也可结合进行。
3.训练数据和测试数据,提高准确率,根据过拟合或者欠拟合,对网络结构做出调整,调参。
机器学习应用举例:搜索引擎,广告推荐,广告优化。自学习问题。
先从第一步开始如何确定机器学习问题?
1.分类还是回归。
分析具体要采用什么模型来解决该问题?
根据输入数据判断是有监督模型还是无监督模型?
线性模型,神经网络,支持向量机,决策树,贝叶斯分类器。
K均值,主成分分析PCA,。
不管是什么模型,其构建过程,评价方式都是有套路的。广泛与适用性。
模型的评估方法是:根据测试误差,来估计泛化误差。泛化误差最大,则最好。
第一步:确定输入数据集X。划分训练集和测试集。
将数据集X分为训练集Train和测试集Test。如何划分呢?主要有三种方法,留出法,交叉验证法,自助法。
留出法:两个集合互斥,73开。最好是采取分层抽样的方法,从而保证两个集合中的各类样本比例一致。常用是2/3-4/5的比例分。
交叉验证法:将X分为K个子集,每次取K-1个子集作为训练集,一个为测试集,进行K次{训练和测试},最后返回K个测试结果的均值。测试结果指的是K次训练,每个模型的测试率。这是评估该模型在该数据集下的结果。模型是指网络结构,那K个模型,要选择测试率最高的一个吗?
自助法:已知数据集X,经过放回采样,采样N次构成训练集T,X-T为测试集。会产生多个训练集和测试集。适用于数据量小的时候。
第二步:模型评价。
回归任务中的性能度量:
分类任务中的性能度量:
其中的F均为机器模型。D为数据集。
线性模型解析:f=WX+B;X为样本,W,B为参数。目的是确定最好的,W,B。
线性回归问题:
通常X的转置X不是满秩矩阵,所以需要引入正则化。
对数线性回归:lny = wTx + b ; y=g(wTx + b ); 为广义线性回归,g为联系函数。
线性分类问题:将分类任务的真实标记与线性回归模型的预测值联系起来,以二分类任务为例,真实标记为0,1。所以需要将预测值wTx + b转化为0或者1.
对数几率回归:y=1/(1+e^(-z)); z = wTx + b; g为对数几率函数,所以称为对数几率回归。
1.假设y含义为样本X预测正例的可能性。y= 1/(1+e^(-wTx + b)); 则1-y为含义为样本X预测反例的可能性。
2. 目标函数是使每个样本属于其真实概率越大越好。
极大似然法:概率模型的训练过程就是参数估计过程,参数估计有两个学派:频率主义学派认为参数未知,但却客观固定,可通过优化似然函数确定参数值;贝叶斯学派认为参数是未观察到的随机变量,其本身也有分布,可假定参数服从一个先验分布,基于观测到的数据计算参数的后验分布。根据数据采样来估计概率分布参数的经典方法。
1.假设样本独立同分布 。
2.这种参数化的方法结果的准确性依赖于所假设的样本概率分布形式是否符合潜在的真实数据分布。
3. 该式是关于参数的高阶可导连续凸函数,根据凸优化,梯度下降法、牛顿法都可求其最优解。不断迭代。直到导数接近零点。
线性判别分析:LDA,一种线性学习方法。二分类应用。将样本投影到一条直线上,同类像近,异类相远。
1.先求得样本集的均值向量和协方差矩阵。
2.将两类样本的中心在直线上的投影求出,包括投影向量,投影协方差矩阵。
3.若要投影点尽可能接近,同类的协方差尽可能小,类中心距离尽可能大。使广义瑞丽商尽可能大即可。
4.最优化问题。
若将W视为一个投影矩阵,则多分类LDA将样本投影到D维空间,D远小于数据原有的特征d。经典监督降维方法。
多分类解决方法:一对多,训练多个分类器。
决策树:分类和回归方法,基于不断判断的方法。详情请看决策树算法介绍。
支持向量机:分类方法,支持向量机详解与实现
神经网络:神经网络模型