吴恩达机器学习课程-作业6-支持向量机（python实现）

Machine Learning(Andrew) ex6-Support Vector Machines

椰汁笔记

Support Vector Machines

• 这个算法是干什么的？
  分类算法，和逻辑回归类似。
• 这个算法的优点是什么？
  这个算法又叫做最大间距分类算法。
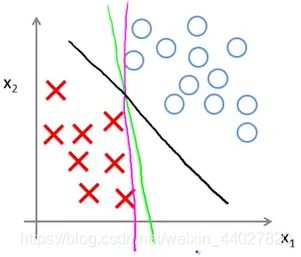
  下面这张图就是很好的解释，对于下面的分类问题之前的逻辑回归的决策边界可能是粉色或者绿色的线。可以看到虽然是成功将数据集分为两部分，但是这样看起来不是那么地自然，分离地比较勉强。
  对于支持向量机，它地决策边界边一定会是黑色地线。可以看到它的分类更加的自然。原因是这个决策边界拥有离训练样本最大的最短距离。这就是支持向量机的优势，这样分类的鲁棒性更好。
  
• 为什么能做到最大间距呢？
  要说清楚这个问题，我们先要了解它的优化目标
  之前的逻辑回归的优化目标是（先不考虑正则化）
  $$J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$
  $$\text{当}y=1\text{，需要使}{\theta }^{T}x>>0\text{，此时的函数为}J(\theta )=-log\frac{1}{1+e^{-z}}\text{，图像如下}$$
  
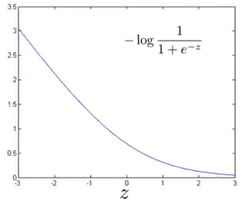
  支持向量机的优化函数做了右图的修改，为粉线部分。1左侧为线性的。可以看到这样改没有改变函数的大致走势，之所以这样改是为了提升计算效率。
  $$\text{当}y=0\text{，需要使}{\theta }^{T}x<<0\text{，此时的函数为}J(\theta )=log\frac{1}{1+e^{-z}}\text{，也做同样的修改图像如下}$$
  
  可以看到改后的损失函数发生了变化，支持向量机的目标函数为
  $$J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}cos{t}_1({\theta }^T{x}^{(i)})-(1-y^{(i)})cos{t}_2({\theta }^T{x}^{(i)})]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$
  再次稍作变形，同时乘以m，除以lambda不影响优化的最后结果
  $$\begin{gathered} J(\theta )=C\sum _{i=1}^m[-y^{(i)}cos{t}_1({\theta }^T{x}^{(i)})-(1-y^{(i)})cos{t}_2({\theta }^T{x}^{(i)})]+\frac{1}{2}\sum _{j=1}^n{\theta }_j^2 \\ 这里的C可以理解为\frac{1}{\lambda }，这个参数的位置只是说明了给哪部分更大的权重 \end{gathered}$$
  下面我们可以理解为什么是最大间距了，要优化的目标函数可以简化为
  $$\begin{gathered} \underset{\theta }{\min }J(\theta )=\frac{1}{2}\sum _{j=1}^n{\theta }_j^2=\frac{1}{2}||\theta |{|}^2 \\ \theta x^{(i)}>>1,if{y}^{(i)}=1;\theta x^{(i)}<<1,if{y}^{(i)}=0 \\ 而\theta x^{(i)}=||\theta ||\ast ||x||\ast cos\alpha ,\alpha 为两个向量的夹角 \end{gathered}$$
  要求出目标函数最小的theta，必须时两个向量的夹角无限接近0度，也就是theta向量和x向量平行，但是注意决策边界和theta向量是垂直的，也就是说x和决策边界是垂直的。这样就可以保证决策边界离数据间距最大，因为|x|cosa就最大，也就是决策边界的值。
  下面这张图就很清楚的说明了p增大就是间距增大。
  
• 这个算法还有什么不同之处呢？
  新的特征构造方法，核函数。
  之前对于非线性的情况，我们使用添加高次多项式特征来实现，这样做的缺点就是随着次数的增大计算量会非常大。
  支持向量机使用通过标记的方式来构造特征
  $$\begin{gathered} Given(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\dots ,(x^{(m)},y^{(m)}) \\ Choose{l}^{(1)}=x^{(1)},l^{(2)}=x^{(2)},\dots ,l^{(m)}=x^{(m)} \\ Givenx:f_1=kernel(x,l^{(1)}),f_2=kernel(x,l^{(2)}),\dots ,f_m=kernel(x,l^{(m)}) \end{gathered}$$
  这样就得到了m个特征，通常选标记点都是直接从数据中选。
  这样的道理是什么呢？这里的核函数是用来度量数据点与标记点的距离，我的理解是分类就是由离某类样本的距离确定的，因此是合理的。

上面对支持向量机的理解是非常宏观的，具体细节还需要深入学习。后面的实现上也没有涉及算法具体，直接调用使用，感觉没什么难度。

• 1.1 Visualizing the datasetyu

第一个数据集的数据是可以线性分类的，先来可视化一下数据，因为要反复画图，封装一下散点图的绘制

def plot_scatter(x1, x2, y):
    """
    绘制散点图
    :param x1: ndarray,横坐标数据
    :param x2: ndarray,纵坐标数据
    :param y: ndarray,标签
    :return: None
    """
    plt.scatter(x1, x2, c=y.flatten())
    plt.xlabel("x1")
    plt.ylabel("X2")
    
data1 = sio.loadmat("data\\ex6data1.mat")
X = data1["X"]
y = data1["y"]
plot_scatter(X[..., 0], X[..., 1], y)
plt.show()

我们运用SVM算法进行分类，这里用的是sklearn这个库的实现，先引入

from sklearn import svm

下面直接进行模型的创建和训练，C就是我们的参数，可以自己指定核函数，这里直接用线性的也就是没有核函数，因为是线性可分的

    model = svm.SVC(C=1, kernel='linear')
    model.fit(X, y.ravel())

下面画出决策边界，这里需要反复用到，因此也封装一下。这里因为考虑到决策边界不一定是直线，所以我们画等高线的方法实现。

def plot_boundary(model, X, title):
    """
    绘制决策边界
    :param model: ,训练好的模型
    :param X: ndarray,训练数据
    :param title: str,图片的题目
    :return: None
    """
    x_max, x_min = np.max(X[..., 0]), np.min(X[..., 0])
    y_max, y_min = np.max(X[..., 1]), np.min(X[..., 1])
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 1000), np.linspace(y_min, y_max, 1000))
    p = model.predict(np.concatenate((xx.ravel().reshape(-1, 1), yy.ravel().reshape(-1, 1)), axis=1))
    plt.contour(xx, yy, p.reshape(xx.shape))
    plt.title(title)

    plot_boundary(model, X, "SVM Decision Boundary with C = 1 (Example Dataset 1)")
    plt.show()

可以看到分类结果还可以，而且当C=1时，异常点没有影响到分类效果。

修改C到100,可以看到异常点影响到了分类的效果。有点点过拟合的味道，具体的我们最后总结。

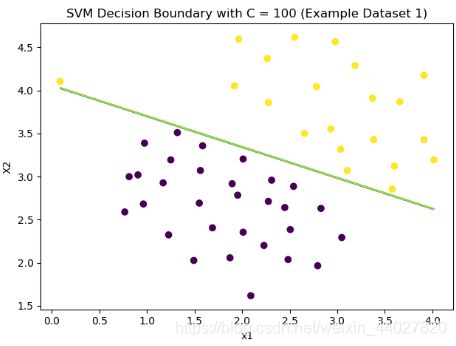
• 1.2 SVM with Gaussian Kernels

可视化第二个数据

    data2 = sio.loadmat("data\\ex6data2.mat")
    X = data2['X']
    y = data2['y']
    plot_scatter(X[..., 0], X[..., 1], y)
    plt.show()

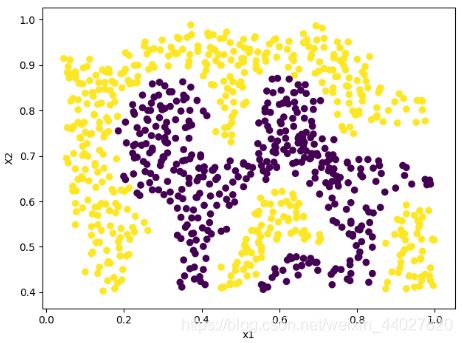
可以看到这里的数据不是线性可分的，因此需要使用核函数了。
高斯核函数是一个常用的选择
$$K_{gaussian}(x^{(i)},x^{(j)})=exp(-\frac{||x^{(i)}-x^{(j)}|{|}^2}{2{\sigma }^2})=exp(-\frac{{\sum }_{k=1}^n(x_k^{(i)}-x_k^{(j)})}{2{\sigma }^2})$$

def gaussian_kernel(x1, x2, sigma):
    return np.exp(-np.sum(np.power(x1 - x2, 2)) / (2 * sigma ** 2))

测试一下

print(gaussian_kernel(np.array([1, 2, 1]), np.array([0, 4, -1]), 2.))
#0.32465246735834974

下面对数据2进行分类，使用高斯核函数。sklearn.svm.SVC中并没有直接的高斯核函数，我么可以通过使用rbf函数配合gamma参数实现，rbf和高斯核函数大致相同，只是将底部换成了gamma，详细可以参考这篇博客

    data2 = sio.loadmat("data\\ex6data2.mat")
    X = data2['X']
    y = data2['y']
    sigma = 0.1
    gamma = 1 / (2 * np.power(sigma, 2))
    plot_scatter(X[..., 0], X[..., 1], y)
    model = svm.SVC(C=1, kernel='rbf', gamma=gamma)
    model.fit(X, y.ravel())
    plot_boundary(model, X, "SVM (Gaussian Kernel) Decision Boundary (Example Dataset 2)")
    plt.show()

可以说分类效果是非常的nice了

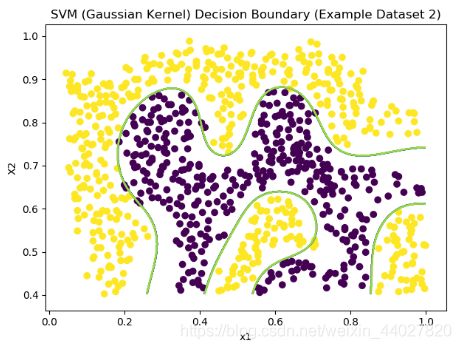
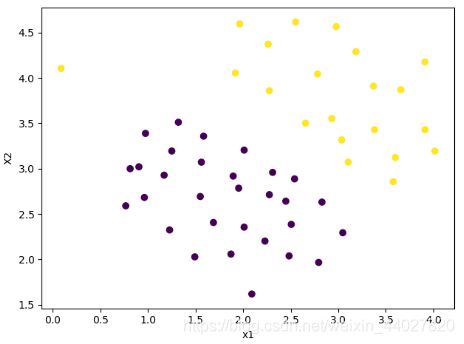
下面继续第三组数据，老规矩先可视化

    data3 = sio.loadmat("data\\ex6data3.mat")
    X = data3['X']
    y = data3['y']
    plot_scatter(X[..., 0], X[..., 1], y)
    plt.show()

可以看到这里的存在多个异常数据，这里的参数选择就非常重要了。

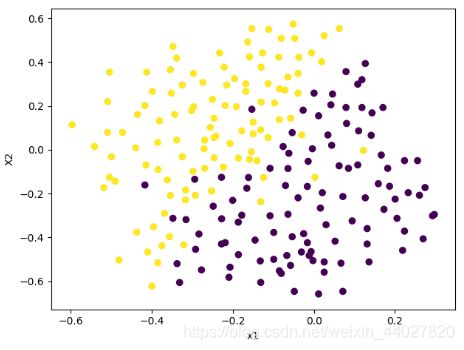
为了达到更好的效果，我们对参数进行选取，C和sigma怎么选取好呢，我们可以不断训练不同的C和sigma的组合通过交叉验证集的量化值(F1-score)来选出最好的选择。这里的C和sigma都从0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30中选，我们因此需要遍历。

    Xval = data3['Xval']
    yval = data3['yval']
    xx, yy = np.meshgrid(np.array([0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]), np.array([0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]))
    parameters = np.concatenate((xx.ravel().reshape(-1, 1), yy.ravel().reshape(-1, 1)), axis=1)
    score = np.zeros(1)
    for C, sigma in parameters:
        gamma = 1 / (2 * np.power(sigma, 2))
        model = svm.SVC(C=C, kernel='rbf', gamma=gamma)
        model.fit(X, y.ravel())
        score = np.append(score, model.score(Xval, yval.ravel()))
    res = np.concatenate((parameters, score[1:].reshape(-1, 1)), axis=1)
    index = np.argmax(res, axis=0)[-1]
    print("the best choice of parameters:C=", res[index][0], ",sigma=", res[index][1], ",score=", res[index][2])
    #the best choice of parameters:C= 1.0 ,sigma= 0.1 ,score= 0.965

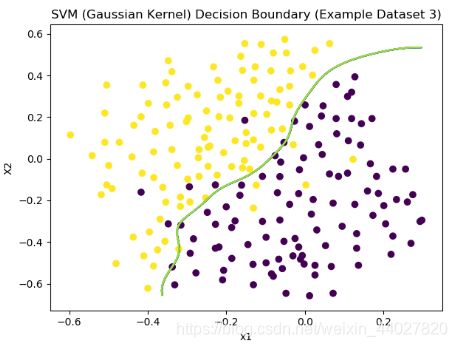
选出的C=1，sigma=0.1时，模型得分最高。以此训练模型，画出决策边界

plot_boundary(model, X, "SVM (Gaussian Kernel) Decision Boundary (Example Dataset 3)")

---

Spam Classification

下面是个关于垃圾邮件分类的半实战项目

• 2.1 Preprocessing Emails

首先我们需要对邮件进行处理

 - 所有字母小写化
 - 移除html标签,eg:

 - 将所有的URL用httpaddr代替
 - 将所有的邮箱用emailaddr代替
 - 将所有的数字用number代替
 - 将所有的$符号用dollar代替
 - 提取每个词的词干
 - 移除多余的空白字符

代替的部分我们使用正则表达式去完成，词干提取使用nltk.stem.porter.PorterStemmer实现。

def process_email(content):
    """
    处理邮件文本
    :param content: str,邮件文本
    :return: list,单词列表
    """
    content = content.lower()
    content = re.sub(r'<.*>', '', content)  # 移除html标签
    content = re.sub(r'http[s]?://.+', 'httpaddr', content)  # 移除url
    content = re.sub(r'[\S]+@[\w]+.[\w]+', 'emailaddr', content)  # 移除邮箱
    content = re.sub(r'[\$][0-9]+', 'dollar number', content)  # 移除$,解决dollar和number连接问题
    content = re.sub(r'\$', 'dollar number', content)  # 移除单个$
    content = re.sub(r'[0-9]+', 'number', content)  # 移除数字
    content = re.sub(r'[\W]+', ' ', content)  # 移除字符
    words = content.split(' ')
    if words[0] == '':
        words = words[1:]  # 分开时会导致开始空格处多出一个空字符
    porter_stemmer = PorterStemmer()
    for i in range(len(words)):
        words[i] = porter_stemmer.stem(words[i])  # 提取词干
    return words

一般会将邮件的单词进行编码，用数字去代替，以便于实现特征的向量化。
这里的数字是由全部数据集的出现的比较多的单词进行排序的，作业中直接提供了。我们直接完成单词到序号的映射。

def mapping(word, vocab):
    """
    单词映射为编号
    :param word: str,单词
    :param vocab: list,编号 表
    :return: int,编号
    """
    for i in range(len(vocab)):
        if word == vocab[i]:
            return i
    return None

• 2.2 Extracting Features from Emails

特征提取就是运用刚才上面的两步内容，实现从邮件到特征向量的转化。

def email_features(email, vocab):
    """
    邮件单词列表转化为特征向量
    :param email: list,邮件的单词列表
    :param vocab: list,编号表
    :return: ndarray,特征向量
    """
    features = np.zeros((len(vocab, )))
    for word in email:
        index = mapping(word, vocab)
        if index is not None:
            features[index] = 1
    return features

• 2.3 Training SVM for Spam Classification

作业中后面没有用到上面的，直接提供了处理好的训练数据，但是推荐大家实现。我这里直接训练模型，这里由于数据量还是比较大，这里不用核函数效果更好，具体的选择方法我在最后总结。

    train_data = sio.loadmat("data\\spamTrain.mat")
    train_X = train_data['X']  # (4000,1899)
    train_y = train_data['y']  # (4000,1)
    test_data = sio.loadmat("data\\spamTest.mat")
    test_X = test_data['Xtest']  # (1000,1899)
    test_y = test_data['ytest']  # (1000,1)
    model = svm.SVC(kernel='linear')  # 这里的n比较大，选用线性核函数效果好
    model.fit(train_X, train_y.ravel())
    print(model.score(train_X, train_y.ravel()), model.score(test_X, test_y.ravel()))
    #0.99975 0.978

下面我们来使用作业给到的邮件例子来试试，对于这个分类正确。

    x = email_features(process_email(open("data\\emailSample2.txt").read()), vocab)
    print(model.predict(x.reshape(1, -1)))#[0]

---

这里来总结一下

• 模型量化评价方法
  三个指标precision，recall，F1 score
  对于一个二分类问题

predict\ actual	1	0
1	True Positive	False Positive
0	False Negative	True Negative

$$\begin{gathered} precision=\frac{TruePositive}{TruePositive+FalsePositive} \\ recall==\frac{TruePositive}{TruePositive+FalseNegative} \\ F1score=\frac{2\ast precision\ast recall}{precision+recall} \end{gathered}$$
精度就是假定都被预测成1，实际上为1的
召回率就是实际为1，预测为1的
这两个值都要高，模型才好，因此F1score就是衡量模型好坏的一个指标，兼顾了精度和召回率。

• 支持向量机的参数选择
  对于C，C越大，可以理解为lambda越小，会出现lower bias和high variance的问题就是过拟合；C越小，可以理解为lambda越大，会出现high bias和low variance的问题就是欠拟合。
  对于高斯函数的sigma，sigma越大，特征变化越平滑，会出现high bias和low variance的问题就是欠拟合；sigma越小，特征变化越陡峭，会出现lower bias和high variance的问题就是过拟合。
  如何选择核函数？

No kernel(linear kernel)	guassian kernel
n large,m small	n small, m large

另外：
当特征数量相对于训练集数量很大时，使用逻辑回归或者是使用线性核函数的支持向量机
当特征数量很少，训练集数据量一般，使用高斯核函数的支持向量机
当特征数量很少，训练集数据很大，可以考虑添加更多特征，然后使用逻辑回归或者是使用线性核函数的支持向量机

---

完整的代码会同步 在我的github

欢迎指正错误