# 回归、拟合算法心得
根据斯坦福机器学习公开课整理的一点体会。记录了概念性的一些理解 ,具体的定义和证明还需要参阅有关资料。
线性拟合
被拟合的样本几乎分布趋势几乎为直线的时候
很多时候,我们希望通过一些样本来反应总体的特征,因此我们需要拟合曲线来判断总体的情况。
假设有如下这些个样本,看起来各点分布趋于一条直线,因此我们希望通过一条直线来描述该样本所在总体的一些特征,对总体进行预测。一般的方法就是先假设一条直线,如 L=ax+b ,之后再根据前面这些样本,确定最优的 a,b ,所谓最优就是通过这些点计算出合适的 a,b ,使各个点对直线上垂直距离的平方和最小(最小二乘法)。具体的方法是通过迭代来计算的。首先建立一个目标函数,假设是 f(a,b)=最优值 ,之后通过迭代使得 f(a,b) 达到最大或最小点,之后确定此时的 a,b 就是我们拟合直线的参数值。

图1
以图中样本为例,因为我们的判定标准(即最优),转换到函数 f 上来,就是求它的极值(最大或最小),如果 f 是连续可导的,那么极值肯定在它导数为0的位置,因此通过对 f(a,b) 在某一点(假设是 a0,b0 )求导。
根据导数值,可以判断该点是在最优点的左边还是右边,之后根据情况调整参数(如果最优点在左边,那么参数就向左挪一步,反之亦然)。若干次迭代后,可以将参数可以达到一个误差允许的范围内。
挪的步数需要注意,假设出来最优点在左边,步长如果太大,迭代后再计算最优点,可能就跑到右边去了,一下子走多了。但是如果太小了,可能会造成很多步的迭代,耗费时间长。
采用线性回归的前提假设
请参阅参考4中内容
对样本采用线性回归时,模型的形式应该为 y=θTx+ϵ , 其中 ϵ 应该是符合正太分布的。这样,我们才能说这个模型有效。所以,变量 y 也是符合正太分布的。
根据参考4,在用线性回归模型拟合数据之前,首先要求数据应符合或近似符合正态分布,否则得到的拟合函数不正确。 若本身样本不符合正态分布或不近似服从正态分布,则要采用其他的拟合方法,比如对于服从二项式分布的样本数据,可以采用logistics线性回归。
为什么要选择最小二乘法作为最优判定标准
假设拟合的目标直线是 y=θTx+ϵ ,其中 ϵ 是误差项,根据中心极限定理,误差项符合正态分布。之后根据极大似然的概念,算出来的 θ 取值的形式,与最小二乘法算出来的形式正好相同。所以可以认为最小二乘法用来评价最优的概念是合理的。
步长的方法
一般通过对最优值函数求导,可以判断出下一步要移动的方向,但是没有涉及步长的取舍。此时可以用牛顿方法,确定步长。
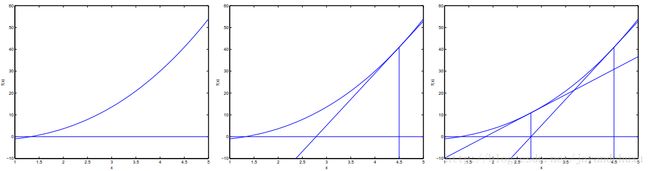
图2
先看一下这个图,假设曲线 f 与 X 轴相交于 (θ0,0) ,并且在这个点附近是凸函数,从附近一点 (θ1,f(θ1)) 做曲线 f 的切线,与 X 轴相交于 (θ2,0) ,因为 f 在 θ1 点出的导数不为0,所以它挪动步长 (θ1−θ2) 后, (θ2,0) 点肯定位于 (θ0,0) 右边,不会超过去。因此,用这种性质来确定步长的大小时,不存在步长过大的情况,而且还是二次收敛的。
被拟合的样本不是线性的时候
被拟合的样本不是线性关系的时候,有时候为了方便也当做线性来处理。
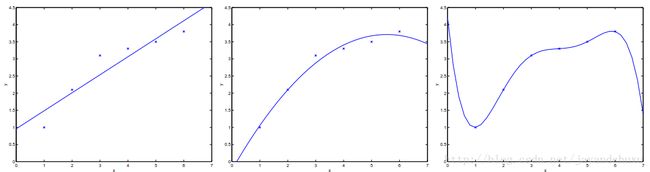
图3
局部加权回归
核心是,如果要预测某一个点,则将这个点相近的点而不是全部的点做线性回归。
从已知推测未知
数据拟合预测,感觉是根据得到样本来预测总体的情况。图1所示的样本,使用一条直线来拟合,图3所示的样本是用曲线来拟合的。通过拟合的结果,可以判断出给定样本的特性。这个概念我理解就通过已知来推测未知。我们可以用已知的数据拟合出一条曲线,来推断出给定数据某一性质的值。也可以对已知数据建立出某套规则,依据某一标准进行分类,再对新的数据,预测出它属于哪个类别。
第一种情况,如图1所示,假设横轴代表的是房屋买卖中房子的面积,纵轴代表它的价格。如此便可以建立出房屋的面积与价格的关系,拟合出一条曲线(直线可以看成是一种特殊的曲线)。当给出某一个房子面积时,可以根据这条曲线推测出相应的价格。
第二种情况的例子,可以用参考图4。通过已知数据,建立一条直线,将其分为两类。之后在有新样本来,根据在直线上方还是下方,来推断出其所在的分类。
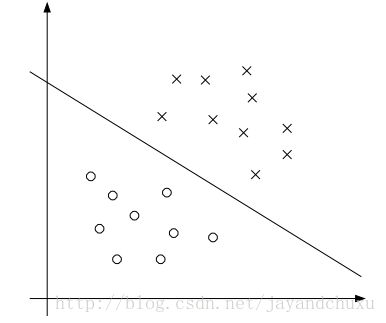
图4
Logistic regression
Logistic回归意思就是根据样本将其分为{0,1}两部分。假设当总体取值为1时的概率为
即
也就是说,在给定 x,θ 后, y 为0,或是1的概率可以表示成:
从上式可以看出来,条件概率P是由 x,y,θ 共同决定的。因此有此建立起来的极大似然函数 L(θ) ,也是有相应参数 x,y,θ 共同决定。当 x,y 已知时,可以通过改变 θ 的值来使得 L(θ) 达到最大值。 L(θ) 的形式如下所示:
可以看出,这个是所有样本在指定 x(i),θ 条件下,取得 y(i) 的概率的乘积。
这里的 hθ(x) 被认为是总体取值为1的概率,也可以看做是取值的期望,因为对目标取值取期望, E(y|x,θ)=1⋅hθ(x)+0⋅(1−hθ(x))=hθ(x)
指数分布族
指数分布族很多分布包括正态分布、对数正态分布、指数分布的概率密度函数都是指数族,除此之外还有泊松分布、gamma分布、beta分布、Dirichlet分布。
指数分布族的形式如下:
指数分布族的分布,都可以写成这种形式,将形式统一后的好处,是可以用一个统一的形式来揭示一些共同的 规律。
根据参考1的解释,指数分布族是为了引出广义线性模型。而广义线性模型正是将指数分布族中的所有成员都作为线性模型的扩展,通过各种非线性的连接函数将线性函数映射到其他空间,从而大大扩大了线性模型可解决的问题。
广义线性模型(Generalized Linear Model, GLM)
GLM 有三个假设:
(1) y|x;θ ~ExponentialFamily(η);给定样本x与参数θ,样本分类y 服从指数分布族中的某个分布;
(2) 给定一个 x,我们需要的函数为 hθ(x)=E[T(y)|x] ;
(3) η=θTx 。
从定义上看,GLM是在指数分布族基础上对相关参数进行了设定,如第三条。可以看成指数分布族的一种特殊形式。从第二个假定看,设定的目标函数是对充分统计量的期望。
我们计算符合正态分布的目标函数时,根据假设2,应该为 hθ(x)=E[T(y)|x] ,其中 T(y)=y (可以从正太分布的广义线性模型里得到),因此 hθ(x)=E[T(y)|x]=E[y|x]=μ 。因为是正态分布,对 y 的期望也就等于 μ 。到了这一步,根据参考1,可以得到广义线性模型中的 hθ(x)=θTx 。
因为广义线性模型中, hθ(x)=E[T(y)|x] 是对充分统计量的期望,因此可以用来进行参与回归问题中目标函数的建立。
线性回归
因为线性回归的误差是符合正态分布的,所以要参照正态分布来处理。得到的 hθ(x) 是对 y 的期望,而 y ~ N(hθ(x),σ2) 。因此可以按照极大似然函数来写出他的目标函数形式:
逻辑回归
逻辑回归中,样本是符合伯努利分布的。广义线性回归中求得的伯努利分布里的函数 hθ(x) 有如下形式: hθ(x)=E[T(y)|x]=E[y|x] (正态分布和伯努利分布中,均存在T(y)=y)。
因此, p(y|x;θ)=(hθ(x))y(1−hθ(x))(1−y) 。此时的目标函数,则可以写成
通过线性回归和逻辑回归,可以看到通过建立GLM中的函数 hθ(x) ,可以构建回归模型中目标函数。
多分类模型-Softmax Regression
原来的伯努利分布是{0,1}分布,即 y∈0,1 ,当遇到多分类问题,即 y∈0,1,2,⋯,k 时,就需要用多分类模型进行处理,这是一个多项式分布问题。而{0,1}分布属于伯努利分布。参考资料1中论述。
参考
- 机器学习-牛顿方法&指数分布族&GLM
- 广义线性模型(Generalized Linear Model)
- 指数分布族
- 线性回归要求因变量服从正态分布