反向传播算法 — Backpropagation
首先,我们以一个双层神经网络为例展示神经网络关于数据标签的计算过程(即前向传播)。

其中, W l W^l Wl和 b l b^l bl分别表示第 l l l层神经元的权重参数和偏置项, s l = W l T a l − 1 + b l s^l = {W^l}^Ta^{l-1} + b^l sl=WlTal−1+bl。 g l g^l gl表示第 l l l层神经元的激活函数,不同层可以选取不同的函数作为激活函数。 a l a^l al表示第 l l l层神经元的输出。本例最终的输出 a 2 a^2 a2即是该神经网络针对数据集 X X X计算得到的预测值 y ^ \hat y y^。
我们可以构建出本神经网络的成本函数 J ( y ^ ) J(\hat y) J(y^)。一个常见的方式是采用最小二乘法,使得残差最小化:
J ( y ^ ) = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 = 1 m ( Y − Y ^ ) T ( Y − Y ^ ) J(\hat y) = \frac {1}{m} \sum\limits_{i=1}^{m}(y_i - \hat y_i)^2 = \frac {1}{m} (Y - \hat Y)^T(Y - \hat Y) J(y^)=m1i=1∑m(yi−y^i)2=m1(Y−Y^)T(Y−Y^)
我们以上图为例,将每层神经元的计算过程以数学公式表示:
{ s 1 = W 1 a 0 + b 1 a 1 = g 1 ( s 1 ) { s 2 = W 2 a 1 + b 2 a 2 = g 2 ( s 2 ) \begin{cases} s^1 = W^1a^0 + b^1 \\ a^1 = g^1(s^1) \end{cases} \\ \begin{cases} s^2 = W^2a^1 + b^2 \\ a^2 = g^2(s^2) \end{cases} {s1=W1a0+b1a1=g1(s1){s2=W2a1+b2a2=g2(s2)
然后,我们来扩展成本函数 J ( y ^ ) J(\hat y) J(y^):
J ( y ^ ) = J ( a 2 ) = J [ g 2 ( s 2 ) ] = J [ g 2 ( W 2 a 1 + b 2 ) ] = J { g 2 [ W 2 g 1 ( W 1 a 0 + b 1 ) + b 2 ] } = J { g 2 [ W 2 g 1 ( W 1 X + b 1 ) + b 2 ] } \begin{aligned} & J(\hat y) = J(a^2) = J[g^2(s^2)] = J[g^2(W^2a^1 + b^2)] = J\{g^2[W^2g^1(W^1a^0 +b^1) + b^2]\} \\ & = J\{g^2[W^2g^1(W^1X +b^1) + b^2]\} \end{aligned} J(y^)=J(a2)=J[g2(s2)]=J[g2(W2a1+b2)]=J{g2[W2g1(W1a0+b1)+b2]}=J{g2[W2g1(W1X+b1)+b2]}
为易于观察,对于不同函数 J , g 2 , g 1 J, g^2, g^1 J,g2,g1,上式采用了不同的括号。上式即嵌套的函数: J ( y ^ ) = J ( g 2 ( g 1 ( X ) ) ) J(\hat y) = J(g^2(g^1(X))) J(y^)=J(g2(g1(X)))。因此,使得成本函数 J ( y ^ ) J(\hat y) J(y^)最小化,我们可以使用梯度下降法得到此例中的自变量 W 1 , W 2 , b 1 W^1, W^2, b^1 W1,W2,b1和 b 2 b^2 b2:
{ W 2 = W 2 − α ▽ J ( W 2 ) b 2 = b 2 − α ▽ J ( b 2 ) { W 1 = W 1 − α ▽ J ( W 1 ) b 1 = b 1 − α ▽ J ( b 1 ) \begin{cases} W^2 = W^2 -\alpha \bigtriangledown J(W^2) \\ b^2 = b^2 -\alpha \bigtriangledown J(b^2) \end{cases} \\ \begin{cases} W^1 = W^1 -\alpha \bigtriangledown J(W^1) \\ b^1 = b^1 -\alpha \bigtriangledown J(b^1) \end{cases} {W2=W2−α▽J(W2)b2=b2−α▽J(b2){W1=W1−α▽J(W1)b1=b1−α▽J(b1)
通用的更新公式为:
W l = W l − α ▽ J ( W l ) b l = b l − α ▽ J ( b l ) W^l = W^l -\alpha \bigtriangledown J(W^l) \\ b^l = b^l -\alpha \bigtriangledown J(b^l) Wl=Wl−α▽J(Wl)bl=bl−α▽J(bl)
上式便是神经网络的反向传播算法,即其学习策略。下面我将继续以文章开始处的例子详细解释反向传播算法。
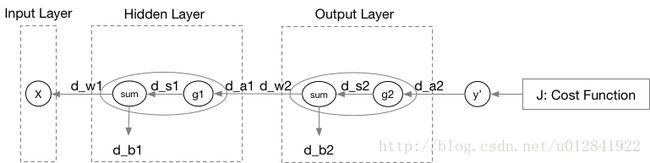
其中, d W l dW^l dWl和 d b l db^l dbl分别表示成本函数 J J J对于 W l W^l Wl和 b l b^l bl的偏导数, d s 1 ds^1 ds1亦是如此。我们可以先计算一下 W 2 W^2 W2和 b 2 b^2 b2的更新公式(因为它们离成本函数最近,偏导的计算量最小):
{ W 2 = W 2 − α ▽ J ( W 2 ) b 2 = b 2 − α ▽ J ( b 2 ) \begin{cases} W^2 = W^2 -\alpha \bigtriangledown J(W^2) \\ b^2 = b^2 -\alpha \bigtriangledown J(b^2) \end{cases} {W2=W2−α▽J(W2)b2=b2−α▽J(b2)
其中, ▽ J ( W 2 ) = ∂ J ∂ W 2 = d W 2 \bigtriangledown J(W^2) = \frac {\partial J}{\partial W^2} = dW^2 ▽J(W2)=∂W2∂J=dW2, ▽ J ( b 2 ) = ∂ J ∂ b 2 = d b 2 \bigtriangledown J(b^2) = \frac {\partial J}{\partial b^2} = db^2 ▽J(b2)=∂b2∂J=db2。
d a 2 = [ d a 1 2 d a 2 2 ⋮ d a l 2 2 ] = [ ∂ J ∂ a 1 2 ∂ J ∂ a 2 2 ⋮ ∂ J ∂ a l 2 2 ] = [ − 2 m ( y 1 i − a 1 i 2 ) − 2 m ( y 2 i − a 2 i 2 ) ⋮ − 2 m ( y l 2 i − a l 2 i 2 ) ] da^2 = \begin{bmatrix} da^2_1 \\ da^2_2 \\ \vdots \\ da^2_{l_2} \end{bmatrix} = \begin{bmatrix} \frac {\partial J}{\partial a^2_1} \\ \frac {\partial J}{\partial a^2_2} \\ \vdots \\ \frac {\partial J}{\partial a^2_{l_2}} \end{bmatrix} = \begin{bmatrix} - \frac {2}{m}(y_{1i} - a^2_{1i}) \\ - \frac {2}{m}(y_{2i} - a^2_{2i}) \\ \vdots \\ - \frac {2}{m}(y_{{l_2}i} - a^2_{{l_2}i}) \end{bmatrix} da2=⎣⎢⎢⎢⎡da12da22⋮dal22⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡∂a12∂J∂a22∂J⋮∂al22∂J⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎡−m2(y1i−a1i2)−m2(y2i−a2i2)⋮−m2(yl2i−al2i2)⎦⎥⎥⎥⎤
其中, l 2 l_2 l2表示神经网络第2层的神经元数目, J = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 J = \frac {1}{m} \sum\limits_{i=1}^{m}(y_i - \hat y_i)^2 J=m1i=1∑m(yi−y^i)2。
d s 2 = [ d s 1 2 d s 2 2 ⋮ d s l 2 2 ] = [ d a 1 2 g 2 ′ ( s 1 2 ) d a 2 2 g 2 ′ ( s 2 2 ) ⋮ d a l 2 2 g 2 ′ ( s l 2 2 ) ] = [ g 2 ′ ( s 1 2 ) 0 … 0 0 g 2 ′ ( s 2 2 ) … 0 ⋮ 0 0 … g 2 ′ ( s l 2 2 ) ] [ d a 1 2 d a 2 2 ⋮ d a l 2 2 ] = [ g 2 ′ ( s 1 2 ) 0 … 0 0 g 2 ′ ( s 2 2 ) … 0 ⋮ 0 0 … g 2 ′ ( s l 2 2 ) ] d a 2 ds^2 = \begin{bmatrix} ds^2_1 \\ ds^2_2 \\ \vdots \\ ds^2_{l_2} \end{bmatrix} = \begin{bmatrix} da^2_1g^{2\prime}(s^2_1) \\ da^2_2g^{2\prime}(s^2_2) \\ \vdots \\ da^2_{l_2}g^{2\prime}(s^2_{l_2}) \end{bmatrix} = \begin{bmatrix} g^{2\prime}(s^2_1) & 0 & \dots & 0 \\ 0 & g^{2\prime}(s^2_2) & \dots & 0 \\ \vdots \\ 0 & 0 &\dots & g^{2\prime}(s^2_{l_2}) \end{bmatrix} \begin{bmatrix} da^2_1 \\ da^2_2 \\ \vdots \\ da^2_{l_2} \end{bmatrix} = \begin{bmatrix} g^{2\prime}(s^2_1) & 0 & \dots & 0 \\ 0 & g^{2\prime}(s^2_2) & \dots & 0 \\ \vdots \\ 0 & 0 &\dots & g^{2\prime}(s^2_{l_2}) \end{bmatrix} da^2 ds2=⎣⎢⎢⎢⎡ds12ds22⋮dsl22⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡da12g2′(s12)da22g2′(s22)⋮dal22g2′(sl22)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡g2′(s12)0⋮00g2′(s22)0………00g2′(sl22)⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡da12da22⋮dal22⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡g2′(s12)0⋮00g2′(s22)0………00g2′(sl22)⎦⎥⎥⎥⎤da2
然后,求 d W 2 dW^2 dW2和 d b 2 db^2 db2:
d W 2 = [ d w 11 2 d w 12 2 … d w 1 l 1 2 d w 21 2 d w 22 2 … d w 2 l 1 2 ⋮ d w l 2 1 2 d w l 2 2 2 … d w l 2 l 1 2 ] = [ d s 1 2 a 1 1 d s 1 2 a 2 1 … d s 1 2 a l 1 1 d s 2 2 a 1 1 d s 2 2 a 2 1 … d s 2 2 a l 1 1 ⋮ d s l 2 2 a 1 1 d s l 2 2 a 2 1 … d s l 2 2 a l 1 1 ] = [ d s 1 2 d s 2 2 ⋮ d s l 2 2 ] [ a 1 1 a 2 1 … a l 1 1 ] = d s 2 a 1 T dW^2 = \begin{bmatrix} dw^2_{11} & dw^2_{12} & \dots & dw^2_{1l_1} \\ dw^2_{21} & dw^2_{22} & \dots & dw^2_{2l_1} \\ \vdots \\ dw^2_{l_21} & dw^2_{l_22} & \dots & dw^2_{l_2l_1} \end{bmatrix} = \begin{bmatrix} ds^2_1a^1_1 & ds^2_1a^1_2 & \dots & ds^2_1a^1_{l_1} \\ ds^2_2a^1_1 & ds^2_2a^1_2 & \dots & ds^2_2a^1_{l_1} \\ \vdots \\ ds^2_{l_2}a^1_1 & ds^2_{l_2}a^1_2 & \dots & ds^2_{l_2}a^1_{l_1} \\ \end{bmatrix} = \begin{bmatrix} ds^2_1 \\ ds^2_2 \\ \vdots \\ ds^2_{l_2} \end{bmatrix} \begin{bmatrix} a^1_1 & a^1_2 & \dots & a^1_{l_1} \end{bmatrix} = ds^2{a^1}^T dW2=⎣⎢⎢⎢⎡dw112dw212⋮dwl212dw122dw222dwl222………dw1l12dw2l12dwl2l12⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡ds12a11ds22a11⋮dsl22a11ds12a21ds22a21dsl22a21………ds12al11ds22al11dsl22al11⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡ds12ds22⋮dsl22⎦⎥⎥⎥⎤[a11a21…al11]=ds2a1T
d b 2 = [ d b 1 2 d b 2 2 ⋮ d b l 2 2 ] = [ d s 1 2 d s 2 2 ⋮ d s l 2 2 ] = d s 2 db^2 = \begin{bmatrix} db^2_1 \\ db^2_2 \\ \vdots \\ db^2_{l_2} \end{bmatrix} = \begin{bmatrix} ds^2_1 \\ ds^2_2 \\ \vdots \\ ds^2_{l_2} \end{bmatrix} = ds^2 db2=⎣⎢⎢⎢⎡db12db22⋮dbl22⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡ds12ds22⋮dsl22⎦⎥⎥⎥⎤=ds2
对于 W 1 W^1 W1和 b 1 b^1 b1的更新公式:
{ W 1 = W 1 − α ▽ J ( W 1 ) b 1 = b 1 − α ▽ J ( b 1 ) \begin{cases} W^1 = W^1 -\alpha \bigtriangledown J(W^1) \\ b^1 = b^1 -\alpha \bigtriangledown J(b^1) \end{cases} {W1=W1−α▽J(W1)b1=b1−α▽J(b1)
其中, ▽ J ( W 1 ) = d s 1 a 0 T \bigtriangledown J(W^1) = ds^1 {a^0}^T ▽J(W1)=ds1a0T, ▽ J ( b 1 ) = d s 1 \bigtriangledown J(b^1) = ds^1 ▽J(b1)=ds1(推导过程同上)。其中:
d s 1 = [ g 1 ′ ( s 1 1 ) 0 … 0 0 g 1 ′ ( s 2 1 ) … 0 ⋮ 0 0 … g 1 ′ ( s l 1 1 ) ] d a 1 ds^1 = \begin{bmatrix} g^{1\prime}(s^1_1) & 0 & \dots & 0 \\ 0 & g^{1\prime}(s^1_2) & \dots & 0 \\ \vdots \\ 0 & 0 &\dots & g^{1\prime}(s^1_{l_1}) \end{bmatrix} da^1 ds1=⎣⎢⎢⎢⎡g1′(s11)0⋮00g1′(s21)0………00g1′(sl11)⎦⎥⎥⎥⎤da1
d a 1 = [ d a 1 1 d a 2 1 ⋮ d a l 1 1 ] = [ d s 2 T [ w 11 2 w 21 2 … w l 2 1 2 ] T d s 2 T [ w 12 2 w 22 2 … w l 2 2 2 ] T ⋮ d s 2 T [ w 1 l 1 2 w 2 l 1 2 … w l 2 l 1 2 ] T ] = W 2 T d s 2 da^1 = \begin{bmatrix} da^1_1 \\ da^1_2 \\ \vdots \\ da^1_{l_1} \end{bmatrix} = \begin{bmatrix} {ds^2}^T \begin{bmatrix} w^2_{11} & w^2_{21} & \dots & w^2_{l_21}\end{bmatrix}^T \\ {ds^2}^T \begin{bmatrix} w^2_{12} & w^2_{22} & \dots & w^2_{l_22}\end{bmatrix}^T \\ \vdots \\ {ds^2}^T \begin{bmatrix} w^2_{1l_1} & w^2_{2l_1} & \dots & w^2_{l_2l_1}\end{bmatrix}^T \end{bmatrix} = {W^2}^Tds^2 da1=⎣⎢⎢⎢⎡da11da21⋮dal11⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡ds2T[w112w212…wl212]Tds2T[w122w222…wl222]T⋮ds2T[w1l12w2l12…wl2l12]T⎦⎥⎥⎥⎥⎤=W2Tds2
因此,根据链式规则可得更为通用的公式:
d s l = g l ′ ( s l ) W l + 1 T d s l + 1 d s l a s t = g l a s t ′ ( s l a s t ) ∂ J ∂ a l a s t ds^l = g^{l\prime}(s^l){W^{l+1}}^Tds^{l+1} \\ ds^{last} = g^{last\prime}(s^{last}) \frac {\partial J}{\partial a^{last}} dsl=gl′(sl)Wl+1Tdsl+1dslast=glast′(slast)∂alast∂J
最后,我将本例的前向传播和反向传播的图示结合起来,并给出完整的反向传播更新公式。

{ W l = W l − α ▽ J ( W l ) = W l − α d s l a l − 1 T b l = b l − α ▽ J ( b l ) = b l − α d s l { d s l = g l ′ ( s l ) W l + 1 T d s l + 1 d s l a s t = g l a s t ′ ( s l a s t ) ∂ J ∂ a l a s t \begin{aligned} & \begin{cases} W^l = W^l -\alpha \bigtriangledown J(W^l) = W^l - \alpha ds^l {a^{l-1}}^T\\ b^l = b^l -\alpha \bigtriangledown J(b^l) = b^l - \alpha ds^l \end{cases} \\ & \begin{cases} ds^l = g^{l\prime}(s^l){W^{l+1}}^Tds^{l+1} \\ ds^{last} = g^{last\prime}(s^{last}) \frac {\partial J}{\partial a^{last}} \end{cases} \end{aligned} {Wl=Wl−α▽J(Wl)=Wl−αdslal−1Tbl=bl−α▽J(bl)=bl−αdsl{dsl=gl′(sl)Wl+1Tdsl+1dslast=glast′(slast)∂alast∂J