全连接神经网络的前向传播和反向传播推导(配图理解)
什么是全连接神经网络?
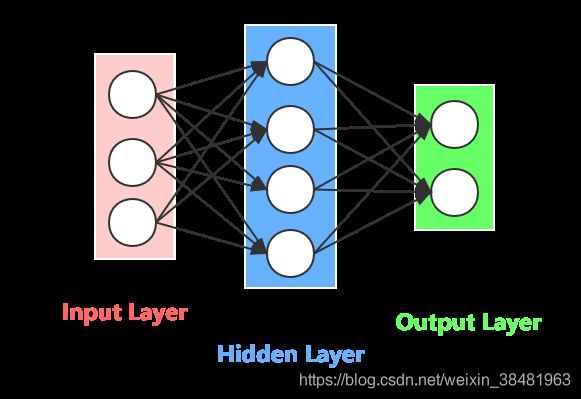
全连接神经网络是指任意两个相邻层之间的神经元全部互相连接。如下图所示:
如何计算全连接神经网络的输出?
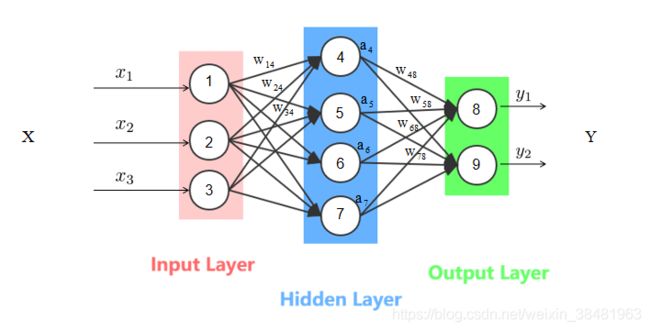
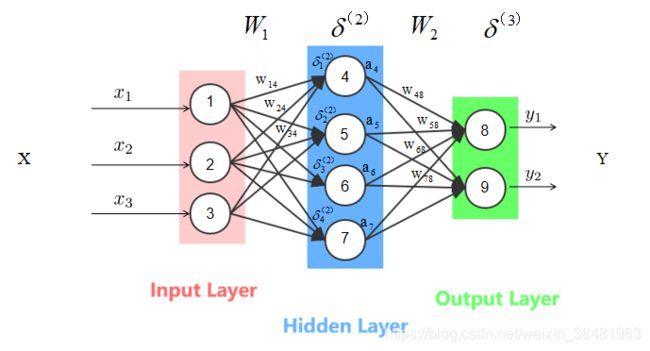
在进行计算前,我们先对一些变量进行说明,如下图所示:
首先是整个神经网络的输入,我们用 x 1 , x 2 , x 3 . . . x n x_1,x_2,x_3...x_n x1,x2,x3...xn 来表示神经网络的输入,在上图中输入是: x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3 。为了方便计算我们还可以用向量表示:
X = [ x 1 x 2 x 3 ] X= \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right] X=⎣⎡x1x2x3⎦⎤
其次是神经网络的权重,我们用 w i j w_{ij} wij 表示,其中 i 是源神经元节点编号, j 是目的神经元节点编号, w i j w_{ij} wij 表示神经元 i 跟 神经元 j 连接的权重。在上图中,节点1根节点4之间的权重为 w 14 w_{14} w14 。同样输入层和隐层之间的权重矩阵以及隐层和输出层之间的权重矩阵也可以用向量表示:
W 1 = [ w 14 w 24 w 34 w 15 w 25 w 35 w 16 w 26 w 36 w 17 w 27 w 37 ] W 2 = [ w 48 w 58 w 68 w 78 w 49 w 59 w 69 w 79 ] W_1 = \left[ \begin{matrix} w_{14} & w_{24} & w_{34} \\ w_{15} & w_{25} & w_{35} \\ w_{16} & w_{26} & w_{36} \\ w_{17} & w_{27} & w_{37} \\ \end{matrix} \right] W_2 = \left[ \begin{matrix} w_{48} & w_{58} & w_{68} & w_{78} \\ w_{49} & w_{59} & w_{69} & w_{79} \\ \end{matrix} \right] W1=⎣⎢⎢⎡w14w15w16w17w24w25w26w27w34w35w36w37⎦⎥⎥⎤W2=[w48w49w58w59w68w69w78w79]
需要注意的是权重矩阵不是随便排列的,这个在下面会提到。
之后是神经网络隐层的输出,我们用 a 1 , a 2 , . . . a l a_1,a_2,...a_l a1,a2,...al 表示,在上图中,隐藏层的输出为: a 4 , a 5 , a 6 , a 7 a_4,a_5,a_6,a_7 a4,a5,a6,a7 ,为了能更好的理解,我们直接用节点编号作为下标。用向量表示为:
a ⃗ = [ a 4 a 5 a 6 a 7 ] \vec{a} =\left[ \begin{matrix} a_4 \\ a_5 \\ a_6 \\ a_7 \end{matrix} \right] a=⎣⎢⎢⎡a4a5a6a7⎦⎥⎥⎤
最后是神经网络的输出,我们用 y 1 , y 2 , . . . y m y_1,y_2,...y_m y1,y2,...ym 来表示,在上图中输出是: y 1 , y 2 y_1,y_2 y1,y2, 我们同样可以用向量表示:
Y = [ y 1 y 2 ] Y = \left[\begin{matrix} y_1 \\ y_2 \end{matrix} \right] Y=[y1y2]
既然我们已经将整个神经网络的输入、权重、中间变量、输出全部介绍完了,接下来,我们真正开始介绍如何从输入经过一系列计算得到输出。
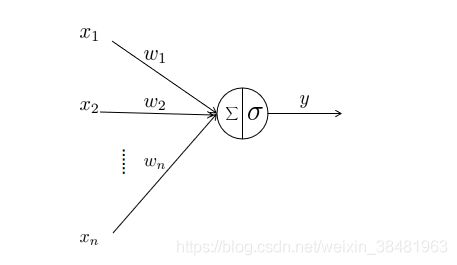
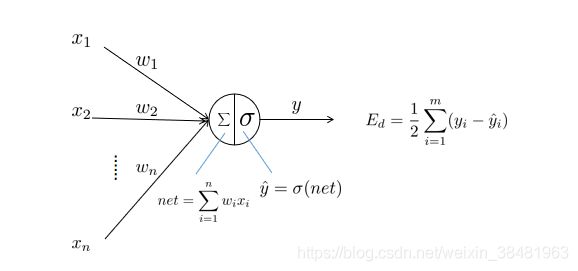
首先看一张图:
这张图展示了经过神经元的数据如何进行计算并输出。
首先是神经元的输入: x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn ,然后是跟每一个输入所对应的权重: w 1 , w 2 , . . . w n w_1,w_2,...w_n w1,w2,...wn ,神经元中的两个符号分别代表两种对输入数据的操作,首先是 ∑ \sum ∑ 求和符号,它代表的是输入数据跟权重的乘积累和,即: ∑ i = 1 n x i w i \sum_{i=1}^n x_iw_i ∑i=1nxiwi ,我们用 n e t net net 表示,即 n e t = ∑ i = 1 n x i w i net=\sum_{i=1}^n x_iw_i net=∑i=1nxiwi ;另一个符号 σ \sigma σ 代表的是一个激活函数,前一步的输出作为激活函数的输入,经过激活函数的计算后得到输出 y y y 。
激活函数不懂的同学可自行百度,这里不再赘述。只需要知道激活函数是神经网络引入的非线性因素,目的是使神经网络可以解决非线性问题。
激活函数有很多种,这里我们以sigmoid函数为例,即:
σ ( x ) = 1 1 + e − x (1) \sigma(x) = \frac{1}{1+e^{-x}} \qquad \tag{1} σ(x)=1+e−x1(1)
那么经过神经元的输出为:
y = σ ( n e t ) = σ ( ∑ i = 1 n x i w i ) = 1 1 + e − ∑ i = 1 n x i w i (2) \begin{aligned} y &= \sigma(net) \\ &= \sigma(\sum_{i=1}^n x_iw_i) \\ &= \frac{1}{1+e^{-\sum_{i=1}^n x_iw_i}} \end{aligned} \tag{2} y=σ(net)=σ(i=1∑nxiwi)=1+e−∑i=1nxiwi1(2)
这个公式别看最后计算挺复杂,其实只有两步运算。
- 神经元输入跟对应权重乘积再累加
- 将上一步结果经过激活函数得到神经元输出
上面介绍的是单个神经元的输入输出计算,接下来我们结合具体的例子再来理解一下:
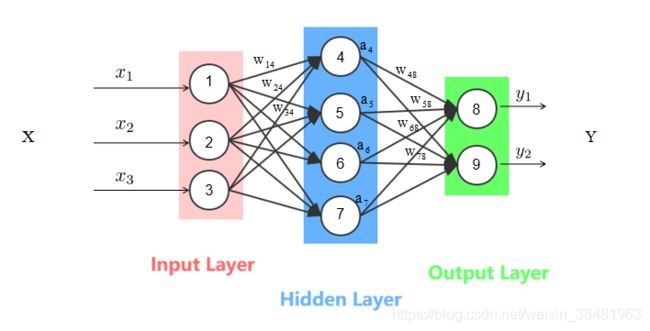
还是这张图,这里我们来计算一下隐藏层节点4的输出 a 4 a_4 a4:
a 4 = σ ( n e t ) = σ ( x 1 w 14 + x 2 w 24 + x 3 w 34 ) (3) \begin{aligned} a_4 &= \sigma(net) \\ &= \sigma(x_1w_{14}+x_2w_{24}+x_3w_{34}) \end{aligned} \tag{3} a4=σ(net)=σ(x1w14+x2w24+x3w34)(3)
同理我们可以计算出隐藏层所有节点的输出 a 4 , a 5 , a 6 , a 7 a_4,a_5,a_6,a_7 a4,a5,a6,a7 ,之后我们再来计算一下输出层节点8的输出值 y 1 y_1 y1 :
y 1 = σ ( a 4 w 48 + a 5 w 58 + a 6 w 68 + a 7 w 78 ) (4) y_1 = \sigma(a_4w_{48}+a_5w_{58}+a_6w_{68}+a_7w_{78}) \tag{4} y1=σ(a4w48+a5w58+a6w68+a7w78)(4)
同理可计算出 y 2 y_2 y2 :
y 1 = σ ( a 4 w 49 + a 5 w 59 + a 6 w 69 + a 7 w 79 ) (5) y_1 = \sigma(a_4w_{49}+a_5w_{59}+a_6w_{69}+a_7w_{79}) \tag{5} y1=σ(a4w49+a5w59+a6w69+a7w79)(5)
以上就是整个神经元从输入到输出的计算过程。
上面的方法必须逐个计算每个神经元的输入输出,其实我们还可以用更简单的方式–矩阵计算。这里我们把前面介绍的矩阵表达直接拿过来:
X = [ x 1 x 2 x 3 ] W 1 = [ w 14 w 24 w 34 w 15 w 25 w 35 w 16 w 26 w 36 w 17 w 27 w 37 ] X= \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right] W_1 = \left[ \begin{matrix} w_{14} & w_{24} & w_{34} \\ w_{15} & w_{25} & w_{35} \\ w_{16} & w_{26} & w_{36} \\ w_{17} & w_{27} & w_{37} \\ \end{matrix} \right] X=⎣⎡x1x2x3⎦⎤W1=⎣⎢⎢⎡w14w15w16w17w24w25w26w27w34w35w36w37⎦⎥⎥⎤
这样一来,我们就可以更简单的计算隐藏层的输出值:
a ⃗ = σ ( W 1 X ) = σ ( [ w 14 w 24 w 34 w 15 w 25 w 35 w 16 w 26 w 36 w 17 w 27 w 37 ] [ x 1 x 2 x 3 ] ) = σ ( [ x 1 w 14 + x 2 w 24 + x 3 w 34 x 1 w 15 + x 2 w 25 + x 3 w 35 x 1 w 16 + x 2 w 26 + x 3 w 36 ] ) = [ σ ( x 1 w 14 + x 2 w 24 + x 3 w 34 ) σ ( x 1 w 15 + x 2 w 25 + x 3 w 35 ) σ ( x 1 w 16 + x 2 w 26 + x 3 w 36 ) ] = [ a 4 a 5 a 6 a 7 ] (6) \begin{aligned} \vec{a} &= \sigma(W_1X) \\ &= \sigma(\left[ \begin{matrix} w_{14} & w_{24} & w_{34} \\ w_{15} & w_{25} & w_{35} \\ w_{16} & w_{26} & w_{36} \\ w_{17} & w_{27} & w_{37} \\ \end{matrix} \right]\left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right] ) \\ &= \sigma(\left[ \begin{matrix} x_1w_{14}+x_2w_{24}+x_3w_{34} \\ x_1w_{15}+x_2w_{25}+x_3w_{35} \\ x_1w_{16}+x_2w_{26}+x_3w_{36} \\ \end{matrix} \right]) \\ &= \left[ \begin{matrix} \sigma(x_1w_{14}+x_2w_{24}+x_3w_{34}) \\ \sigma(x_1w_{15}+x_2w_{25}+x_3w_{35}) \\ \sigma(x_1w_{16}+x_2w_{26}+x_3w_{36})\end{matrix} \right] \\ &= \left[ \begin{matrix} a_4 \\ a_5 \\ a_6 \\ a_7 \end{matrix} \right] \end{aligned} \tag{6} a=σ(W1X)=σ(⎣⎢⎢⎡w14w15w16w17w24w25w26w27w34w35w36w37⎦⎥⎥⎤⎣⎡x1x2x3⎦⎤)=σ(⎣⎡x1w14+x2w24+x3w34x1w15+x2w25+x3w35x1w16+x2w26+x3w36⎦⎤)=⎣⎡σ(x1w14+x2w24+x3w34)σ(x1w15+x2w25+x3w35)σ(x1w16+x2w26+x3w36)⎦⎤=⎣⎢⎢⎡a4a5a6a7⎦⎥⎥⎤(6)
瞧!该矩阵的第一行不正是我们前面求出的第4个神经元的输出值吗。
同理我们还可以根据矩阵计算出输出层的 Y Y Y 值:
Y = σ ( W 2 a ⃗ ) = σ ( [ w 48 w 58 w 68 w 78 w 49 w 59 w 69 w 79 ] [ a 4 a 5 a 6 a 7 ] ) = σ ( [ a 4 w 48 + a 5 w 58 + a 6 w 68 + a 7 w 78 a 4 w 49 + a 5 w 59 + a 6 w 69 + a 7 w 79 ] ) = [ σ ( a 4 w 48 + a 5 w 58 + a 6 w 68 + a 7 w 78 ) σ ( a 4 w 49 + a 5 w 59 + a 6 w 69 + a 7 w 79 ) ] = [ y 1 y 2 ] (7) \begin{aligned} Y &= \sigma(W_2\vec{a}) \\ &= \sigma(\left[ \begin{matrix} w_{48} & w_{58} & w_{68} & w_{78} \\ w_{49} & w_{59} & w_{69} & w_{79} \\ \end{matrix} \right]\left[ \begin{matrix} a_4 \\ a_5 \\ a_6 \\ a_7 \end{matrix} \right] ) \\ &= \sigma(\left[ \begin{matrix} a_4w_{48}+a_5w_{58}+a_6w_{68}+a_7w_{78} \\ a_4w_{49}+a_5w_{59}+a_6w_{69}+a_7w_{79} \\\end{matrix}\right]) \\ &= \left[ \begin{matrix} \sigma(a_4w_{48}+a_5w_{58}+a_6w_{68}+a_7w_{78}) \\ \sigma(a_4w_{49}+a_5w_{59}+a_6w_{69}+a_7w_{79})\end{matrix}\right] \\ &= \left[ \begin{matrix} y_1 \\ y_2 \end{matrix}\right] \end{aligned} \tag{7} Y=σ(W2a)=σ([w48w49w58w59w68w69w78w79]⎣⎢⎢⎡a4a5a6a7⎦⎥⎥⎤)=σ([a4w48+a5w58+a6w68+a7w78a4w49+a5w59+a6w69+a7w79])=[σ(a4w48+a5w58+a6w68+a7w78)σ(a4w49+a5w59+a6w69+a7w79)]=[y1y2](7)
其中 W 2 W_2 W2 是隐藏层到输出层的权重矩阵, a ⃗ \vec{a} a 是隐藏层输出值。结果跟我们之前的推导一模一样。
到此为止,全连接神经网络的前向计算已经全部推导完毕。
全连接神经网络的反向传播算法推导
我们将所有输出层节点的误差平方和作为目标函数:
E d = 1 2 ∑ i = 1 m ( y i − y ^ i ) 2 (8) E_d=\frac{1}{2}\sum_{i=1}^m(y_i-\hat{y}_i)^2 \tag{8} Ed=21i=1∑m(yi−y^i)2(8)
其中 E d E_d Ed 代表损失函数, m m m 代表输出层神经元个数, y i y_i yi 代表第i个神经元的实际值, y ^ i \hat{y}_i y^i 代表模型预测值。
接下来用梯度下降算法来优化目标函数:
w i j ← w i j − α ∂ E d ∂ w i j (9) w_{ij} \leftarrow w_{ij} - \alpha \frac{\partial{E}_d}{\partial{w}_{ij}} \tag{9} wij←wij−α∂wij∂Ed(9)
这个是我们梯度更新的公式,可以更新任一权重。之后我们会介绍如何用矩阵更新一组权重。
假设 n e t j net_j netj 是神经元节点 j 的加权输入:
n e t j = w 1 j x 1 j + w 2 j x 2 j + . . . + w n j x n j = ∑ i = 1 n w i j x i j (10) \begin{aligned} net_j &= w_{1j}x_{1j}+w_{2j}x_{2j}+...+w_{nj}x_{nj} \\ &= \sum_{i=1}^n w_{ij}x_{ij} \end{aligned} \tag{10} netj=w1jx1j+w2jx2j+...+wnjxnj=i=1∑nwijxij(10)
其中 w i j w_{ij} wij 是第 i 个节点到第 j 个节点的权重, x i j x_{ij} xij 是第 i 个节点到第 j 个节点的输入。
还是前面这张图,希望能通过这张图看清楚 n e t j net_j netj 在神经网络中的位置,在这里 n e t j net_j netj 就相当于上图中的 ∑ \sum ∑ 的位置。通过这张图还要理清楚函数的链式关系:误差 E d E_d Ed 是 y i ^ \hat{y_i} yi^ 的函数, y ^ \hat{y} y^ 是 n e t net net 的函数, n e t net net 是 w i w_i wi 的函数;目的是为了下面的链式求导铺垫。
接下来求损失函数对 $w_{ij} $ 的偏导数:
∂ E d ∂ w i j = ∂ E d ∂ n e t j ∂ n e t j ∂ w i j = ∂ E d ∂ n e t j ∂ ∑ i = 1 n w i j x i j ∂ w i j = ∂ E d ∂ n e t j x i j (11) \begin{aligned} \frac{\partial{E}_d}{\partial{w}_{ij}} &= \frac{\partial{E}_d}{\partial{net_j}} \frac{\partial{net_j}}{\partial{w_{ij}}} \\ &= \frac{\partial{E}_d}{\partial{net_j}} \frac{\partial{\sum_{i=1}^n w_{ij}x_{ij}}}{\partial{w_{ij}}} \\ &= \frac{\partial{E}_d}{\partial{net_j}} x_{ij} \end{aligned} \tag{11} ∂wij∂Ed=∂netj∂Ed∂wij∂netj=∂netj∂Ed∂wij∂∑i=1nwijxij=∂netj∂Edxij(11)
为了求得其偏导数,需要分两种情况进行讨论:输出层和隐层
1.输出层权值训练
∂ E d ∂ n e t j = ∂ E d ∂ y j ^ ∂ y j ^ ∂ n e t j = ∂ ∂ y j ^ 1 2 ∑ i = 1 m ( y i − y ^ i ) 2 ∂ σ ( n e t j ) ∂ n e t j = − ( y j − y j ^ ) y j ^ ( 1 − y j ^ ) (12) \begin{aligned} \frac{\partial{E_d}}{\partial{net_j}} &= \frac{\partial{E_d}}{\partial{\hat{y_j}}}\frac{\partial{\hat{y_j}}}{\partial{net_j}} \\ &= \frac{\partial}{\partial{\hat{y_j}}}\frac{1}{2}\sum_{i=1}^m(y_i-\hat{y}_i)^2 \frac{\partial\sigma(net_j)}{\partial{net_j}} \\ &= -(y_j-\hat{y_j}) \hat{y_j}(1-\hat{y_j}) \end{aligned} \tag{12} ∂netj∂Ed=∂yj^∂Ed∂netj∂yj^=∂yj^∂21i=1∑m(yi−y^i)2∂netj∂σ(netj)=−(yj−yj^)yj^(1−yj^)(12)
这里的 σ \sigma σ 激活函数用的是sigmoid函数,故其导数为 σ ( 1 − σ ) \sigma(1-\sigma) σ(1−σ) ,上式第二行第二项就是这样的来的。
令 δ j = − ∂ E d ∂ n e t j \delta{}_{j} = -\frac{\partial{E_d}}{\partial{net_j}} δj=−∂netj∂Ed ,即:
δ j = ( y j − y j ^ ) y j ^ ( 1 − y j ^ ) (13) \delta{}_{j} = (y_j-\hat{y_j}) \hat{y_j}(1-\hat{y_j}) \tag{13} δj=(yj−yj^)yj^(1−yj^)(13)
最后将上述公式带入梯度下降公式可得:
w i j ← w i j − α ∂ E d ∂ w i j = w i j + α δ j x i j = w i j + α ( y j − y j ^ ) y j ^ ( 1 − y j ^ ) x i j (14) \begin{aligned}w_{ij} &\leftarrow w_{ij} - \alpha \frac{\partial{E_d}}{\partial{w_{ij}}} \\&= w_{ij} + \alpha \delta{}_{j}x_{ij} \\&= w_{ij} + \alpha (y_j-\hat{y_j}) \hat{y_j}(1-\hat{y_j})x_{ij} \\\end{aligned} \tag{14} wij←wij−α∂wij∂Ed=wij+αδjxij=wij+α(yj−yj^)yj^(1−yj^)xij(14)
这个就是更新输出层权值的公式;
2.隐藏层权值训练
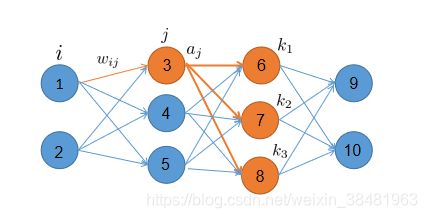
这里我们先定义节点 j 的所有直接下游节点集合为 K K K , 从下图中我们可以明显看出,节点3的直接下游节点为{6,7,8};
(注:图 5只是为了便于理解隐藏层权值训练过程,所有的实际计算均以图 2主)
从上图可以看出,权值 w i j w_{ij} wij 通过影响节点 j 的输出可以直接影响到节点 j 的所有直接下游节点,于是:
∂ E d n e t j = ∑ k ∈ K ∂ E d n e t k ∂ n e t k n e t j = ∑ k ∈ K − δ k ∂ n e t k ∂ a j ∂ a j ∂ n e t j = ∑ k ∈ K − δ k w j k a j ( 1 − a j ) = − a j ( 1 − a j ) ∑ k ∈ K δ k w j k (15) \begin{aligned} \frac{\partial{E_d}}{net_j} &= \sum_{k\in K} \frac{\partial{E_d}}{net_k} \frac{\partial{net_k}}{net_j} \\ &= \sum_{k\in K} -\delta{}_{k} \frac{\partial{net_k}}{\partial{a_j}} \frac{\partial{a_j}}{\partial{net_j}} \\ &= \sum_{k\in K} -\delta{}_{k} w_{jk}a_j(1-a_j) \\ &= -a_j(1-a_j)\sum_{k\in K} \delta{}_{k} w_{jk} \end{aligned} \tag{15} netj∂Ed=k∈K∑netk∂Ednetj∂netk=k∈K∑−δk∂aj∂netk∂netj∂aj=k∈K∑−δkwjkaj(1−aj)=−aj(1−aj)k∈K∑δkwjk(15)
再将 δ j = − ∂ E d ∂ n e t j \delta{}_{j} = -\frac{\partial{E_d}}{\partial{net_j}} δj=−∂netj∂Ed 带入:
δ j = a j ( 1 − a j ) ∑ k ∈ K δ k w j k (16) \delta{}_{j} = a_j(1-a_j)\sum_{k\in K} \delta{}_{k} w_{jk} \tag{16} δj=aj(1−aj)k∈K∑δkwjk(16)
最后带入梯度下降公式:
w i j ← w i j − α ∂ E d ∂ w i j = w i j − α ∂ E d ∂ n e t j ∂ n e t j ∂ w i j = w i j + α δ j x i j = w i j + α a j ( 1 − a j ) x i j ∑ k ∈ K δ k w j k (17) \begin{aligned} w_{ij} &\leftarrow w_{ij} - \alpha \frac{\partial{E_d}}{\partial{w_{ij}}} \\ &= w_{ij} - \alpha \frac{\partial{E}_d}{\partial{net_j}} \frac{\partial{net_j}}{\partial{w_{ij}}} \\ &= w_{ij} + \alpha \delta{}_{j}x_{ij} \\ &= w_{ij} + \alpha a_j(1-a_j)x_{ij}\sum_{k\in K} \delta{}_{k} w_{jk} \\ \end{aligned} \tag{17} wij←wij−α∂wij∂Ed=wij−α∂netj∂Ed∂wij∂netj=wij+αδjxij=wij+αaj(1−aj)xijk∈K∑δkwjk(17)
我们就得到了隐藏层的权值更新公式;
显然通过上面的方法需要一个个更新神经元的权值,非常麻烦;接下来我们介绍用矩阵的方式进行计算。
令:
x ⃗ = [ x 1 x 2 x 3 ] a ⃗ = [ a 4 a 5 a 6 a 7 ] y ^ ⃗ = [ y 1 ^ y 2 ^ ] y ⃗ = [ y 1 y 2 ] W 1 = [ w 14 w 24 w 34 w 15 w 25 w 35 w 16 w 26 w 36 w 17 w 27 w 37 ] W 2 = [ w 48 w 58 w 68 w 78 w 49 w 59 w 69 w 79 ] δ ( 2 ) ⃗ = [ δ 1 ( 2 ) δ 2 ( 2 ) δ 3 ( 2 ) δ 4 ( 2 ) ] δ ( 3 ) ⃗ = [ δ 1 ( 3 ) δ 2 ( 3 ) ] \vec{x} = \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right] \qquad\vec{a} = \left[ \begin{matrix} a_4 \\ a_5 \\ a_6 \\ a_7 \end{matrix} \right] \qquad\vec{\hat{y}} = \left[ \begin{matrix} \hat{y_1} \\ \hat{y_2} \end{matrix} \right] \qquad\vec{y} = \left[ \begin{matrix} y_1 \\ y_2 \end{matrix} \right] \qquad \\ W_1 = \left[ \begin{matrix} w_{14} & w_{24} & w_{34} \\w_{15} & w_{25} & w_{35} \\w_{16} & w_{26} & w_{36} \\w_{17} & w_{27} & w_{37} \\ \end{matrix} \right]\qquad W_2 = \left[ \begin{matrix} w_{48} & w_{58} & w_{68} & w_{78} \\w_{49} & w_{59} & w_{69} & w_{79} \\ \end{matrix} \right] \\\vec{\delta{}^{(2)}} = \left[ \begin{matrix} \delta{}_{1}^{(2)} \\\delta{}_{2}^{(2)} \\ \delta{}_{3}^{(2)} \\ \delta{}_{4}^{(2)} \end{matrix} \right]\qquad\vec{\delta{}^{(3)}} = \left[ \begin{matrix} \delta{}_{1}^{(3)} \\\delta{}_{2}^{(3)} \end{matrix} \right] x=⎣⎡x1x2x3⎦⎤a=⎣⎢⎢⎡a4a5a6a7⎦⎥⎥⎤y^=[y1^y2^]y=[y1y2]W1=⎣⎢⎢⎡w14w15w16w17w24w25w26w27w34w35w36w37⎦⎥⎥⎤W2=[w48w49w58w59w68w69w78w79]δ(2)=⎣⎢⎢⎢⎡δ1(2)δ2(2)δ3(2)δ4(2)⎦⎥⎥⎥⎤δ(3)=[δ1(3)δ2(3)]
将公式13和公式16用向量表示为:
δ ⃗ = y ^ ⃗ ( 1 − y ^ ⃗ ) ( y ⃗ − y ^ ⃗ ) (18) \vec{\delta} = \vec{\hat{y}}(1-\vec{\hat{y}})(\vec{y}-\vec{\hat{y}}) \tag{18} \\ δ=y^(1−y^)(y−y^)(18)
δ ⃗ ( l ) = a ⃗ ( l ) ( 1 − a ⃗ ( l ) ) W T δ ⃗ ( l + 1 ) (19) \vec{\delta}^{(l)} = \vec{a}^{(l)}(1-\vec{a}^{(l)})W^T\vec{\delta}^{(l+1)} \tag{19} δ(l)=a(l)(1−a(l))WTδ(l+1)(19)
权重更新的向量化表示为:
W ← W + α δ ⃗ x ⃗ T (20) \begin{aligned}W \leftarrow W + \alpha \vec{\delta}\vec{x}^T \end{aligned} \tag{20} W←W+αδxT(20)
偏置项更新的向量化表示为:
b ⃗ ← b ⃗ + α δ ⃗ (21) \vec{b} \leftarrow \vec{b} + \alpha \vec{\delta} \tag{21} b←b+αδ(21)
接下来我们举例说明 W 1 , W 2 W_1,W_2 W1,W2 的更新是怎样计算的:
先计算 δ ⃗ ( 3 ) \vec{\delta}^{(3)} δ(3):
δ ⃗ ( 3 ) = y ^ ⃗ ( 1 − y ^ ⃗ ) ( y ⃗ − y ^ ⃗ ) = [ y 1 ^ y 2 ^ ] ( 1 − [ y 1 ^ y 2 ^ ] ) ( [ y 1 y 2 ] − [ y 1 ^ y 2 ^ ] ) = [ y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) ] \begin{aligned}\vec{\delta}^{(3)} &= \vec{\hat{y}}(1-\vec{\hat{y}})(\vec{y}-\vec{\hat{y}}) \\&= \left[ \begin{matrix} \hat{y_1} \\ \hat{y_2} \end{matrix} \right] (1-\left[ \begin{matrix} \hat{y_1} \\ \hat{y_2} \end{matrix} \right])(\left[ \begin{matrix} y_1 \\ y_2 \end{matrix} \right] -\left[ \begin{matrix} \hat{y_1} \\ \hat{y_2} \end{matrix} \right]) \\&= \left[ \begin{matrix} \hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1) \\ \hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)\end{matrix}\right]\end{aligned} δ(3)=y^(1−y^)(y−y^)=[y1^y2^](1−[y1^y2^])([y1y2]−[y1^y2^])=[y^1(1−y^1)(y1−y^1)y^2(1−y^2)(y2−y^2)]
然后更新 W 2 W_2 W2 :
W 2 ← W 2 + α δ ⃗ x ⃗ T = W 2 + α δ ⃗ ( 3 ) a ⃗ T = [ w 48 w 58 w 68 w 78 w 49 w 59 w 69 w 79 ] + α [ y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) ] [ a 4 a 5 a 6 a 7 ] = [ w 48 w 58 w 68 w 78 w 49 w 59 w 69 w 79 ] + α [ y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) a 4 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) a 5 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) a 6 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) a 7 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) a 4 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) a 5 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) a 6 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) a 7 ] = [ w 48 + α y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) a 4 w 58 + α y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) a 5 w 68 + α y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) a 6 w 78 + α y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) a 7 w 49 + α y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) a 4 w 49 + α y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) a 5 w 49 + α y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) a 6 w 49 + α y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) a 7 ] \begin{aligned}W_2 &\leftarrow W_2 + \alpha \vec{\delta}\vec{x}^T \\&= W_2 + \alpha \vec{\delta}{}^{(3)}\vec{a}^T \\&= \left[ \begin{matrix} w_{48} & w_{58} & w_{68} & w_{78} \\w_{49} & w_{59} & w_{69} & w_{79} \\ \end{matrix} \right] + \alpha \left[ \begin{matrix} \hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1) \\ \hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)\end{matrix}\right] \left[ \begin{matrix} a_4 & a_5 & a_6 & a_7 \end{matrix} \right] \\&= \left[ \begin{matrix} w_{48} & w_{58} & w_{68} & w_{78} \\w_{49} & w_{59} & w_{69} & w_{79} \\ \end{matrix} \right] + \alpha \left[ \begin{matrix} \hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)a_4 & \hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)a_5 & \hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)a_6 & \hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)a_7 \\\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)a_4 & \hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)a_5 & \hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)a_6 & \hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)a_7\end{matrix} \right] \\&= \left[\begin{matrix} w_{48}+\alpha\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)a_4 & w_{58}+\alpha\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)a_5 & w_{68}+\alpha\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)a_6 & w_{78}+\alpha\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)a_7 \\ w_{49}+\alpha\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)a_4 & w_{49}+\alpha\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)a_5 & w_{49}+\alpha\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)a_6 & w_{49}+\alpha\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)a_7 \end{matrix}\right]\end{aligned} W2←W2+αδxT=W2+αδ(3)aT=[w48w49w58w59w68w69w78w79]+α[y^1(1−y^1)(y1−y^1)y^2(1−y^2)(y2−y^2)][a4a5a6a7]=[w48w49w58w59w68w69w78w79]+α[y^1(1−y^1)(y1−y^1)a4y^2(1−y^2)(y2−y^2)a4y^1(1−y^1)(y1−y^1)a5y^2(1−y^2)(y2−y^2)a5y^1(1−y^1)(y1−y^1)a6y^2(1−y^2)(y2−y^2)a6y^1(1−y^1)(y1−y^1)a7y^2(1−y^2)(y2−y^2)a7]=[w48+αy^1(1−y^1)(y1−y^1)a4w49+αy^2(1−y^2)(y2−y^2)a4w58+αy^1(1−y^1)(y1−y^1)a5w49+αy^2(1−y^2)(y2−y^2)a5w68+αy^1(1−y^1)(y1−y^1)a6w49+αy^2(1−y^2)(y2−y^2)a6w78+αy^1(1−y^1)(y1−y^1)a7w49+αy^2(1−y^2)(y2−y^2)a7]
之后求 δ ⃗ ( 2 ) \vec{\delta}^{(2)} δ(2) :
δ ⃗ ( 2 ) = a ⃗ ( 2 ) ( 1 − a ⃗ ( 2 ) ) W 2 T δ ⃗ ( 3 ) = [ a 4 a 5 a 6 a 7 ] ( 1 − [ a 4 a 5 a 6 a 7 ] ) [ w 48 w 49 w 58 w 59 w 68 w 69 w 78 w 79 ] [ y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) ] = [ a 4 ( 1 − a 4 ) a 5 ( 1 − a 5 ) a 6 ( 1 − a 6 ) a 7 ( 1 − a 7 ) ] [ w 48 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) + w 49 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) w 58 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) + w 59 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) w 68 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) + w 69 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) w 78 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) + w 79 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) ] = [ a 4 ( 1 − a 4 ) ( w 48 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) + w 49 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) ) a 5 ( 1 − a 5 ) ( w 58 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) + w 59 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) ) a 6 ( 1 − a 6 ) ( w 68 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) + w 69 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) ) a 7 ( 1 − a 7 ) ( w 78 y ^ 1 ( 1 − y ^ 1 ) ( y 1 − y ^ 1 ) + w 79 y ^ 2 ( 1 − y ^ 2 ) ( y 2 − y ^ 2 ) ) ] \begin{aligned}\vec{\delta}^{(2)} &= \vec{a}^{(2)}(1-\vec{a}^{(2)})W_2^T\vec{\delta}^{(3)} \\&= \left[ \begin{matrix} a_4 \\ a_5 \\ a_6 \\ a_7 \end{matrix} \right] (1-\left[ \begin{matrix} a_4 \\ a_5 \\ a_6 \\ a_7 \end{matrix} \right])\left[ \begin{matrix} w_{48} & w_{49} \\ w_{58} & w_{59} \\w_{68} & w_{69} \\ w_{78} & w_{79} \\ \end{matrix} \right] \left[ \begin{matrix} \hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1) \\ \hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)\end{matrix}\right] \\&= \left[ \begin{matrix} a_4(1-a_4) \\ a_5(1-a_5) \\ a_6(1-a_6) \\ a_7(1-a_7) \end{matrix} \right] \left[ \begin{matrix} w_{48}\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)+w_{49}\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2) \\ w_{58}\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)+w_{59}\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2) \\w_{68}\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)+w_{69}\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2) \\w_{78}\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)+w_{79}\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2) \end{matrix} \right] \\&= \left[ \begin{matrix}a_4(1-a_4)(w_{48}\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)+w_{49}\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)) \\a_5(1-a_5)(w_{58}\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)+w_{59}\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)) \\a_6(1-a_6)(w_{68}\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)+w_{69}\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2)) \\a_7(1-a_7)(w_{78}\hat{y}_1(1-\hat{y}_1)(y_1-\hat{y}_1)+w_{79}\hat{y}_2(1-\hat{y}_2)(y_2-\hat{y}_2))\end{matrix} \right]\end{aligned} δ(2)=a(2)(1−a(2))W2Tδ(3)=⎣⎢⎢⎡a4a5a6a7⎦⎥⎥⎤(1−⎣⎢⎢⎡a4a5a6a7⎦⎥⎥⎤)⎣⎢⎢⎡w48w58w68w78w49w59w69w79⎦⎥⎥⎤[y^1(1−y^1)(y1−y^1)y^2(1−y^2)(y2−y^2)]=⎣⎢⎢⎡a4(1−a4)a5(1−a5)a6(1−a6)a7(1−a7)⎦⎥⎥⎤⎣⎢⎢⎡w48y^1(1−y^1)(y1−y^1)+w49y^2(1−y^2)(y2−y^2)w58y^1(1−y^1)(y1−y^1)+w59y^2(1−y^2)(y2−y^2)w68y^1(1−y