复习—线性结构之数组与广义表

数组和广义表都可以看成是 表中数据元素本身也是数据结构的线性表

数组

定义

对于n维数组来说，每个元素都受到n个关系的约束，在每个关系中aj₁j₂…j_n都会有一个直接后继，因此，对于单个关系而言，仍为线性关系。
n维数组可以看为线性表的推广且所有数据元素都属于同一数据类型。

数组一旦被定义，它的维度和维界就不再改变。因此，除了初始化和销毁之外，数组只有存取元素和修改元素的操作
也就意味着不能插入和删除

另外，数组在计算机中存储时有行优先的规定
对于二维数组来说LOC(i，j)=LOC(0,0)+(b₂*i+j)*L
(b₂为第二维的长度，L为单个元素所占存储空间大小)

三维数组按照 页/行/列的顺序存储

对于n维数组
LOC(j₁,j₂,…,j_n)=LOC(0,0,…,0)+(b₂X…Xb_nXj₁+b₃X…Xb_nXj₂+…+b_nXj_n-1+j_n)XL

矩阵的压缩存储

特殊矩阵的压缩存储

特殊矩阵是指：值相同的元素或者非零元素在矩阵中的分布有一定规律的矩阵。

目的是为了节省存储空间，对可以不存储的元素（0或者对称元素）不再存储

常见的例子有对称矩阵和三对角矩阵

对称矩阵的压缩

因为对称矩阵中a_ij=a_ji
所以我们只存储上三角/下三角矩阵（对角线+对角线上/下部分的元素）

存储方法
将上/下三角矩阵存放到一个n(n+1)/2长度的一维数组中，称为对称矩阵的压缩。

对应关系
若存储下三角矩阵，则存储元素a_ij全都有i>=j（1= 当i>=j时，k=i(i-1)/2+j-1
当j>=i时，k=j(j-1)/2+i-1(即用a_ji对应了上三角的a_ij)

此时一位数组sa[k]=a_ij，有了对应关系。

这样的存储方法也适用于三角矩阵
所谓的上（下）三角矩阵就是矩阵的下（上）三角（不包括对角线）中元素都为0或常数c的n阶矩阵。
这样只需要存上（下）三角中的元素再加一个常数C即可压缩三角矩阵。

---

三对角矩阵的压缩

三对角矩阵除了主对角线和主对角线上、下相邻的两条对角线上的元素外，其他元素都为0。 共有n+n-1+n-1=3n-2个要存储的元素

三对角矩阵也是按照行优先的方式压缩到一维数组中

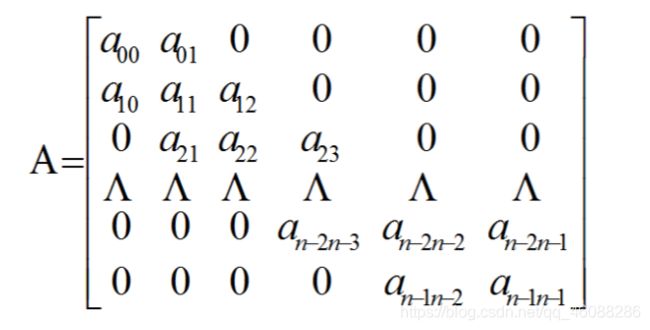
课本上这里的 i，j又从零开始了…

对于a_ij
第i行前有3*i-1个非零元素
本行中第j列前有j-i+1个非零元素
所以k=2*i+j
所以B[2*i+j]=A[i][j]

而且，i=（k+1）/3向下取整、j=k-2i

---

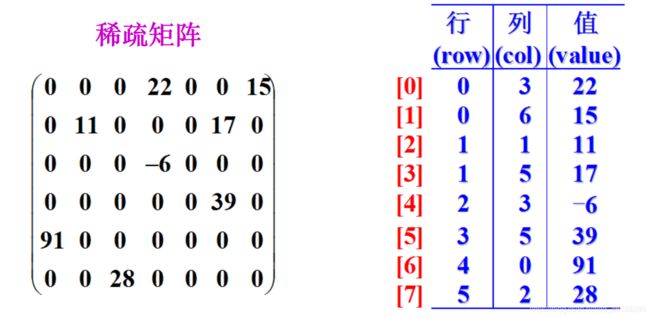
稀疏矩阵的压缩存储

稀疏矩阵0元素>>非零元素且分布无规律的矩阵。

常使用矩阵的稀疏因子来判断，δ=t/m*n（t为非零元素数，m，n为矩阵规格）
当δ<=0.05时，常认为是稀疏矩阵。

稀疏矩阵的存储和特殊矩阵的存储不同

特殊矩阵压缩不需要存储元素位置
而稀疏矩阵元素分布无规律，因此要存储元素所在的位置
且还要存储稀疏矩阵的规格M,N

三元组法

三元组的数据结构如下

class Tnode
{
     
public:
    int i,j; //每个结点的原来的位置
    int e;  // 结点的值
};
class Triple
{
     
public:
    int mu,nu,tu;       //矩阵的规格，和非零元素的个数
    Tnode data[Maxsize+1];//三元组，0号位未使用。
};

因为C语言的数组是行优先存储，所以我们的三元组大都是以行序排列的

---

三元组表示的稀疏矩阵的转置算法

方法1.按照三元组中的列数进行转置

对三元组扫描nu次，第k次对列数为k的项进行操作：将其行号列号互换，顺序存到三元组中。

 T.mu=nu;
    T.nu=mu;
    T.tu=tu;
    if(T.tu)
    {
     
        int q=1;
        for(int clo=1;clo<=nu;clo++)
        {
     
            for(int p=1;p<=tu;p++)
            {
     
                if(data[p].j==clo)
                {
     
                    T.data[q].i=data[p].j;
                    T.data[q].j=data[p].i;
                    T.data[q].e=data[p].e;
                    q++;
                }
            }
        }
    }

时间复杂度为O(nu*tu)
一般的矩阵转置算法的时间复杂度为O(munu)
当tu=munu时，为O(munu^2)
仅适用于tu<nu的情况

方法2.快速转置运算
核心预先确定矩阵每一行第一个非零元素在三元组中的位置，转置时就可以直接放进去。
算法就先不写了，溜了~~

行逻辑连接的顺序表可方便进行稀疏矩阵乘法

十字链表法适用于矩阵加法或减法运算。

---

广义表

定义

顾名思义，广义表是线性表的推广（也称为列表list）因此定义也相仿。
如下
广义表是n(>=0)个表元素组成的有限序列
记作LS=（a₀,a₁,a₂,…,a_n-1）
其中LS为表名，a_i为表元素，它可以是表(称为子表)，也可以是数据元素（称为原子）

常常以大写字母表示广义表，小写字母表示原子

n为表的长度，n=0的广义表为空表

n>0时，表的第一个元素称为广义表的表头(head)，除此之外，其他元素组成的表叫做广义表的表尾(tail)

---

举几个栗子
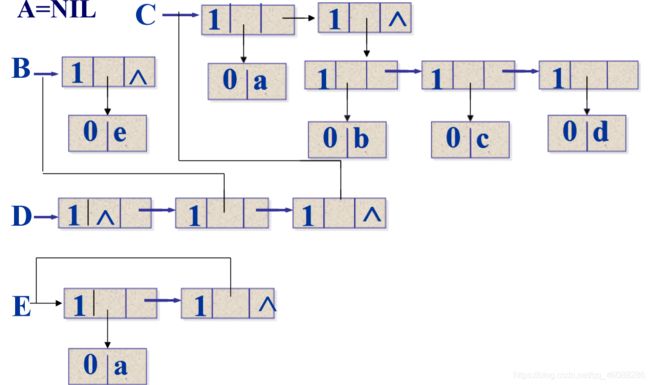
A=()
A为空表，长度为0；
B=(e)
列表B只有一个原子，长度为1
C=(a,(b,c,d))
列表C长度为2，两个元素分别为原子a和子表（b,c,d）
D=(A,B,C)
列表D长度为3,3个元素都为子表
E=(a,E)
列表E长度为2，是一个递归的表
F=( ( ) )
列表F长度为1，元素为空表

注意点
1.列表的元素可能是子表，子表的元素还可以是子表…因此，列表是一个多层次的结构。
2.列表可以被其他列表共享。/ / D中有A,B,C三个子表
3.列表可以为一个递归的表，即列表可以是本身的一个子表。

4.任何一个非空列表其表头可能是原子，也可能是列表，但其表尾一定是列表

存储结构

由于广义表中数据元素可以具有不同的结构，所以很难用顺序结构统一，所以一般使用链式存储结构

需要两种结点：
一是表结点，来表示列表。二是原子结点，来表示原子。
因为列表不空时可以分解成表头和表尾，且根据一对确定的表头和表尾可以确定唯一的列表
因此表结点需要由：标志位、指示表头的指针域、指示表尾的指针域三部分构成
而原子结点只需要：标志位、值域两部分即可。

typedef enum{
     ATOM,LIST}ElemTag;
typedef struct GLNode{
     
        ElemTag tag;
        union{
     
        AtomType atom；
        struct{
     struct GLNode *hp,*tp}ptr;
        };
}*GList;        

该方法的几种情况
1.除空表的表头指针为空外，任何非空列表，其表头指针都指向一个表结点。
且hp指向列表表头，tp指向列表表尾（除非表尾为空，否则必为表结点）

2.容易分清列表中原子和子表所在层次

3.最高层表结点的个数即为表的长度

前面例子用这样的方式表示

---

广义表的深度

即广义表中括号的重数
设非空广义表为LS=(a₁,a₂,…,a_n)
则求LS的深度可分解为n个子问题，即求a_i的深度
若a_i是原子，深度为0,；若a_i是广义表，则继续分解。

LS的深度为a_i深度中最大值+1
空表的深度为1