Matlab神经网络十讲(1): Basic
1. Simple Neural
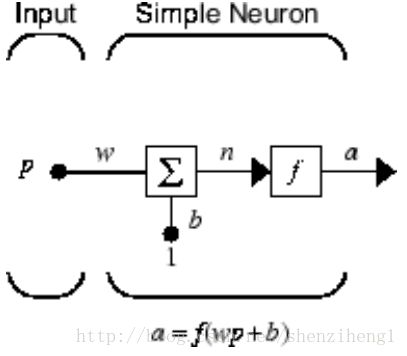First, the scalar input p is multiplied by the scalar weight w to form the product wp,again a scalar. Second, the weighted input wp is added to the scalar bias b to form the
net input n. (In this case, you can view the bias as shifting the function f to the left by an
amount b. The bias is much like a weight, except that it has a constant input of 1.)
Finally, the net input is passed through the transfer function f, which produces the
scalar output a. The names given to these three processes are: the weight function, the
net input function and the transfer function.
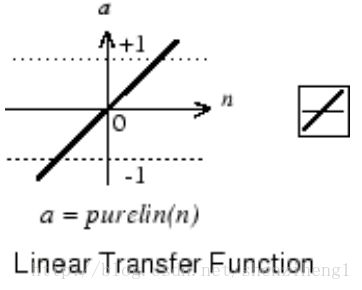
2.Transfer Functions
Neurons of this type are used in the final layer of multilayer networks that are used as function approximators.
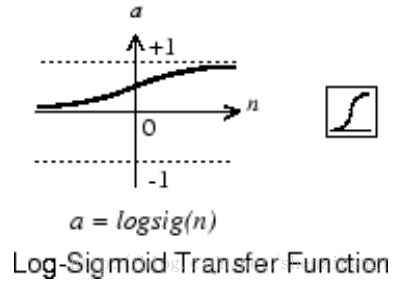The sigmoid transfer function shown below takes the input, which can have any value between plus and minus infinity, and squashes the output into the rang.
This transfer function is commonly used in the hidden layers of multilayer networks, in part because it is differentiable.
3. Neural with multi-inputs
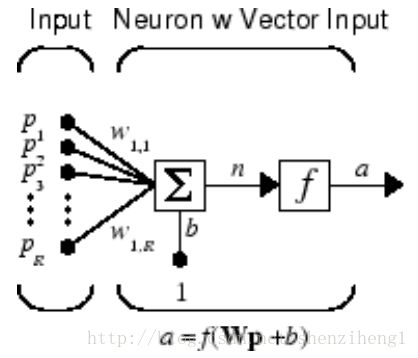
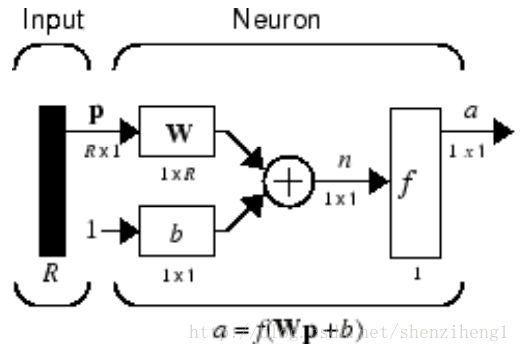
A neuron with a single R-element input vector is shown left.
Here the individual input elements pR are multiplied by weights
wR and the weighted values are fed to the summing junction. Their sum is simply Wp, the dot product of the (single row) matrix W and the vector p.
wR and the weighted values are fed to the summing junction. Their sum is simply Wp, the dot product of the (single row) matrix W and the vector p.
The neuron has a bias b, which is summed with the weighted inputs to form the net input n.
4. Abbreviated Notation
A layer includes the weights, the multiplication and summing operations (here realized as a vector product Wp), the bias b, and the transfer function f. The array of inputs, vector p, is not included in or called a layer.5.Netural Network Achitectures
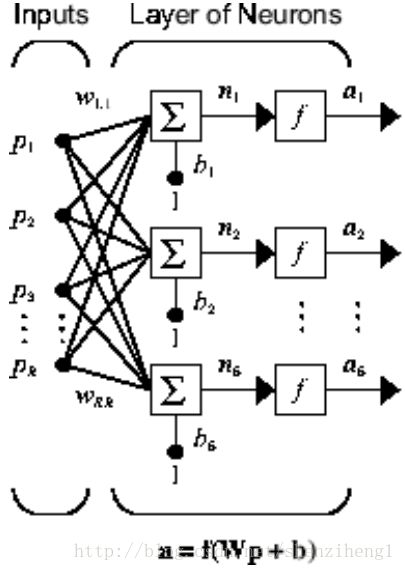
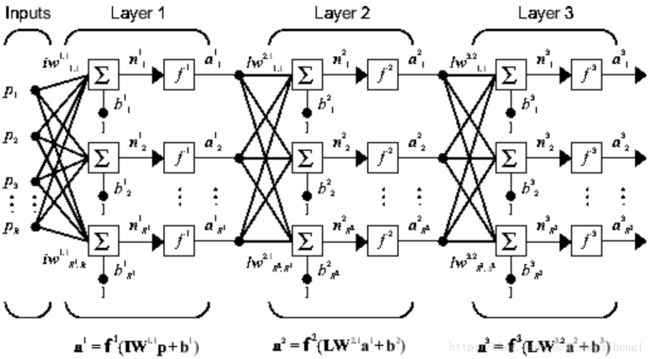
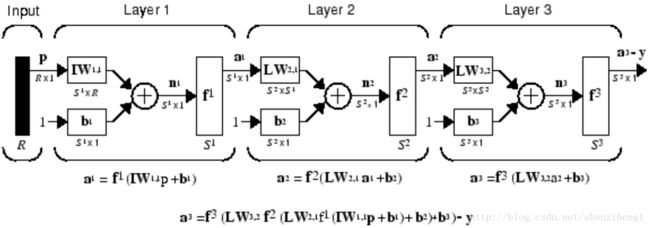
A one-layer network with R input elements and S neurons follows.
In this network, each element of the input vector p is connected to each neuron input through the weight matrix W. The ith neuron has a summer that gathers its weighted inputs and bias to form its own scalar output n(i). The various n(i) taken together form an S-element net input vector n. Finally, the neuron layer outputs form a column vector a. The expression for a is shown at the bottom of the figure.
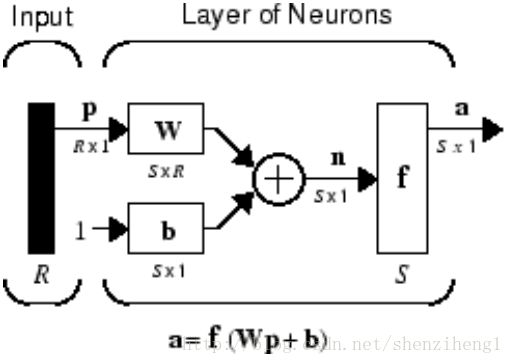
The S neuron R-input one-layer network also can be drawn in abbreviated notation.
Here p is an R-length input vector, W is an S × R matrix, a and b are S-length vectors. As defined previously, the neuron layer includes the weight matrix, the multiplication operations, the bias vector b, the summer, and the transfer function blocks.
6. Input and Layer
We will call weight matrices connected to inputs input weights; we will call weight matrices connected to layer outputs layer weights. Further, superscripts are used to identify the source (second index) and the destination (first index) for the various weights and other elements of the network.
As you can see, the weight matrix connected to the input vector p is labeled as an input weight matrix (IW1,1) having a source 1 (second index) and a destination 1 (first index). Elements of layer 1, such as its bias, net input, and output have a superscript 1 to say that they are associated with the first layer.
The network shown above has R1 inputs, S1 neurons in the first layer, S2 neurons in the second layer, etc. It is common for different layers to have different numbers of neurons. A constant input 1 is fed to the bias for each neuron.
The layers of a multilayer network play different roles. A layer that produces the network output is called an output layer. All other layers are called hidden layers. The three-layer network shown earlier has one output layer (layer 3) and two hidden layers (layer 1 and layer 2). Some authors refer to the inputs as a fourth layer. This toolbox does not use that designation.
Multiple-layer networks are quite powerful. For instance, a network of two layers, where the first layer is sigmoid and the second layer is linear, can be trained to approximate any function (with a finite number of discontinuities) arbitrarily well.
7. Input and Output Processing Functions
Network inputs might have associated processing functions. Processing functions transform user input data to a form that is easier or more efficient for a network.
7.1 Input Processing Functions
mapminmax : transforms input data so that all values fall into the interval [−1, 1]. This can speed up learning for many networks.
removeconstantrows : removes the rows of the input vector that correspond to input elements that always have the same value, because these input elements are not providing any useful information to the
network.
network.
fixunknowns : which recodes unknown data (represented in the user's data with NaN values) into a numerical form for the network. fixunknowns preserves information about which values are known and which are unknown.
7.2 Output Processing Functions
Output processing functions are used to transform user-provided target vectors for network use.Then, network outputs are reverse-processed using the same functions to produce output data with the same characteristics as the original user-provided targets.
Both mapminmax and removeconstantrows are often associated with network outputs. However, fixunknowns is not. Unknown values in targets (represented by NaN values) do not need to be altered for network use.