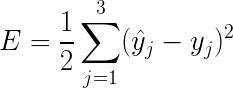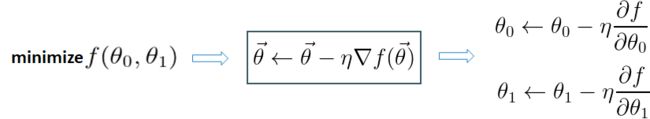第二周第一天第二天第三天第四天第五天
开会:
分好任务,wyl做语言模型,我和yyp做声学模型,还是想先看懂那个ARST系统的代码,然后做修改完成!
二:安装了feature特征包
三:ASRT可以运行
四:训练数据,关于项目文档、ppt,准备开会内容
五:看代码
举例---使用清华大学公开语音数据集data_thchs30(wav音频)
train:20000 / 2
dev:1786 / 2
test:4990 / 2
(一)人工神经网络发展
1、M-P神经元
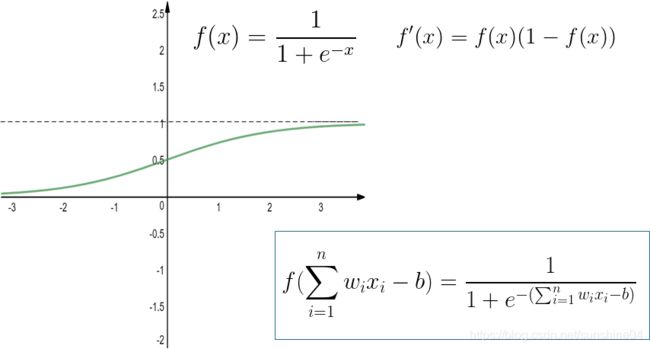
2、激活函数(响应函数)
将输入值映射为输出值”0“(神经元抑制)或”1“(神经元兴奋),
常用Sigmoid函数,把可能在较大范围内变化的输入值挤压到(0,1)范围内
3、感知机和多层感知机网络
单层感知机:2层神经元(输入层+输出层(M-P神经元))【输出层是功能神经元】
特点:
只能处理线性可分问题(异或问题就没办法处理)
影响:掀起人工神经网络第一波浪潮,对于简单的异或问题就没办法处理,就”退潮“了
多层感知机:多层:①单隐层(一层隐藏层)②多隐层(多层隐藏层) 【隐藏层和输出层都是拥有激活函数的功能神经元】
特点:
①全连接(每一层神经元都和前一层的所有神经元都有连接,不存在同层和跨层连接,且连接权各不相同)
②前馈神经网络
缺点:(前馈)当时很难进行训练学习,没有一个比较有效的学习方式,学习参数。
------->于是,后面【见下面的神经网络的第二次热潮】提出BP算法,用Sigmoid激活函数(使得神经网络有解决非线性问题的能力)
要解决非线性可分问题,就需要考虑使用多层感知机。
第一次打破非线性诅咒的是深度学习之父杰弗里·辛顿(Geoffrey Hinton),其在1986年发明了适用于多层感知器(MLP)的BP算法(反向传播算法),并采用Sigmoid激活函数进行非线性映射,有效解决了非线性分类和学习的问题。该方法引起了神经网络的第二次热潮。
1989 年。 Yann LeCun(乐困)利用反向传播的思想发明了卷积神经网络-LeNet,并将其用于数字识别,且取得了较好的成绩。
不幸的是,浪潮仅仅持续到90年代中期(mid-1990s)就”退潮“了
原因:
2006年左右,Hinton辛顿再次宣称他知道大脑是如何工作的,并提出了非监管的预训练和深度信念网的想法。使用这种策略,人们能够训练比以前更深层次的网络,促使“神经网络”更名为“深度学习”。
引起了神经网络的第三次热潮。
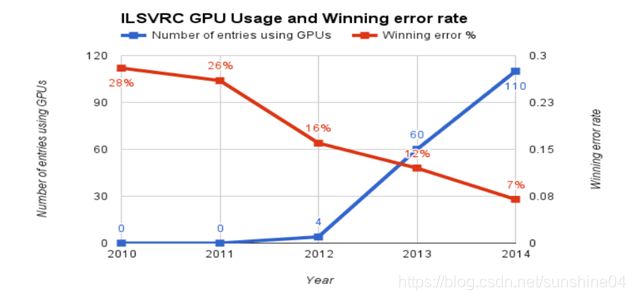
真正神经网络的大突破是在2012年,
2012年已经提出了GPU
on imagenet图像数据集(斯坦福大学制作), 举办了一个比赛
根据图片,随着GPU块数使用增多,随着改善网络结构,错误率在下降。
到现在讲完人工神经网络发展历史,在讲BP算法之前:
- How to build neural networks?
-
Learning or Training Process?
-
How to update parameters ?
-
How to efficiently update weights and bias ?
(1)How to build neural networks?
神经网络的学习过程就是调整人工参数,使得学习参数不断接近最优的过程
- 人工确定的参数:
隐含层数目;每个隐含层神经元数目;每个神经元的激活函数;损失函数E; 学习率 ; Batsch size ; Epoch
- 需要学习的参数:(开始在网络中是随机初始化的)
Weights ; Bias
(2) Learning or Training Process?
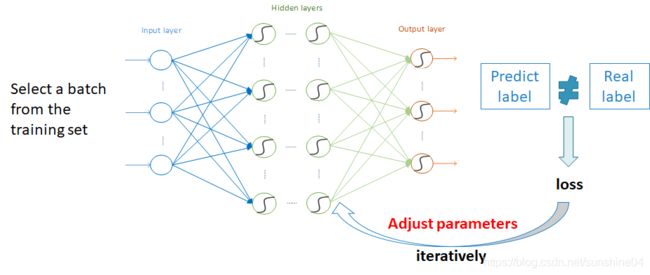
准备好数据(分为训练集和验证集),举个例子:
xi代表声学模型的输入(数据预处理之后的特征矩阵),yi代表声学模型的输出(拼音列表)
图解:假设训练集10000条wav文件,batch size =100,代表每次送入100条语音特征矩阵到神经网络,然后查看这100条的loss值,反向传播调整学习参数 w和b,然后这就是一次迭代。然后再传入batch size =100条语音,重复上述过程。当训练完10000条训练集的语音,这算是一轮,one epoch,一轮训练显然不够!!!验证集查看训练效果
打乱训练集,再选择一个batch,然后再训练 one epoch.验证集查看训练效果
打乱训练集,再选择一个batch,然后再训练 one epoch.验证集查看训练效果
训练停止:
1)人工确定epoch数目
2)每一轮确定在验证集上的loss,如果多轮没有下降,可以停止。
举个例子:
1)Stochastic Gradient Descent, SGD 随机梯度下降法
Basically, in SGD, we are using the loss of 1 sample to update parameters at each iteration
For this example, one epoch of training update the weight and bias 10000 times
每次放入一个样本batch size =1,一轮更新10000次连接权和偏置
2)Batch Gradient Descent, BGD batch梯度下降法
In BGD, we are using the mean of the loss of ALL examples in training set at each iteration
For this example, one epoch of training update the weight and bias 1 time
每次放入全部样本batch size =10000,一轮更新1次连接权和偏置
3)Mini-batch Gradient Descent mini-batch梯度下降法
Mini-batch gradient descent uses n samples(instead of 1 sample in SGD) at each iteration.
For this example, one epoch of training update the weight and bias 10000 / n times
每次放入全部样本batch size = n ,一轮更新(10000 / n )次连接权和偏置
(3)How to update parameters ?
其实是一个非常复杂的函数,常常用 梯度下降法
什么是梯度?
沿着梯度下降方向,容易找到函数最大值
即:沿着负梯度下降(是不是就是梯度上升?)方向,容易找到函数最小值
Θ = (Θ0 , Θ1)T
Θ(k+1) = Θ(k) + λd [ 下降方向: d = - Δf (Θ) ]
λ 步长 : 在神经网络中称为 " 学习率 ".
步长太大,可能越过最低点
步长太小,可能迭代次数太多
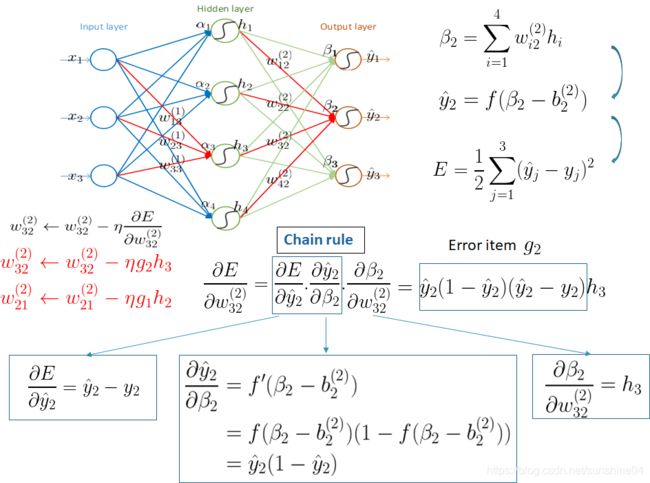
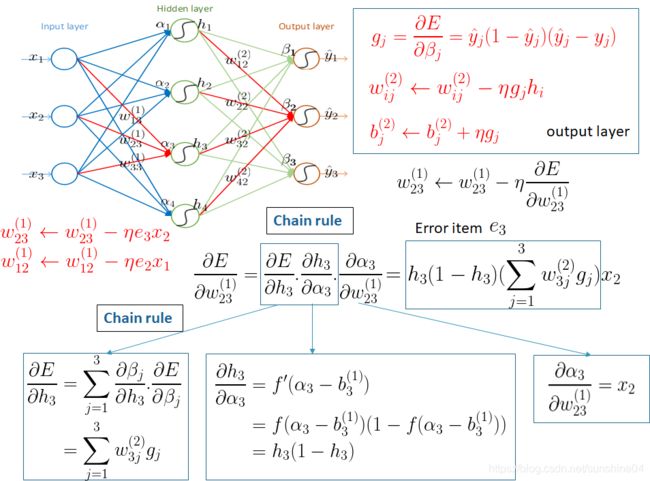
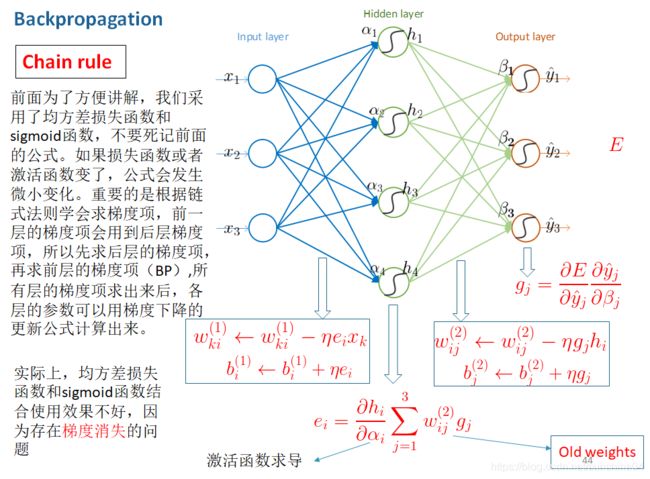
4、BP算法(反向传播算法)
(4) How to efficiently update weights and bias ?
举例如下:
由后向前计算,由后(反向传播)
1)先求输出层的每一个神经元的残差
2)再求输出层的前一个隐含层的残差
3)以此类推.....直到更新完所有的参数
MLP:多层感知机
将 softmax层作为输出层。(输出层的激活函数使用softmax函数)
总结:
sigmoid将一个real value映射到(0,1)的区间(当然也可以是(-1,1)),这样可以用来做二分类。
![]()
而softmax把一个k维的real value向量(a1,a2,a3,a4…)映射成一个(b1,b2,b3,b4…)其中bi是一个0-1的常数,然后可以根据bi的大小来进行多分类的任务,如取权重最大的一维。
![]()
————————————————
版权声明:本文为CSDN博主「trayfour」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/u014422406/article/details/52805924
多层感知机MLP的限制:
全连接------>使得连接权太多,要求内存大、计算强
如何减少网络中参数的数量?------->CNN
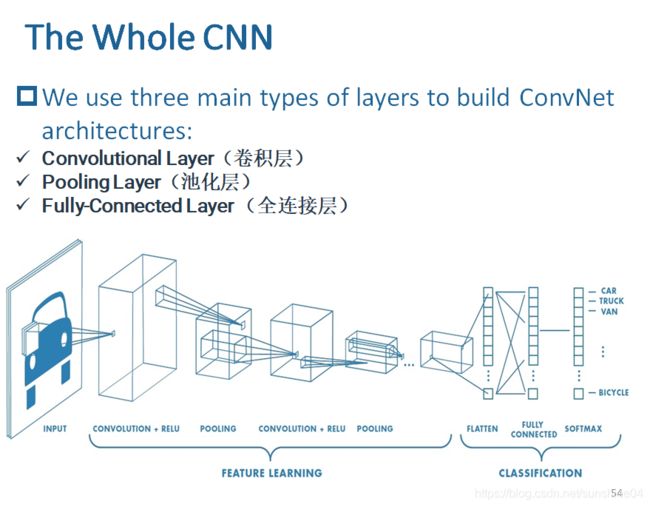
(二)深度学习
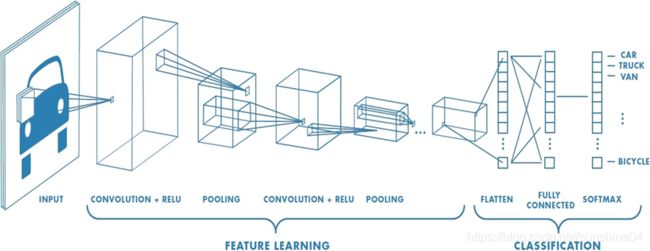
1、CNN
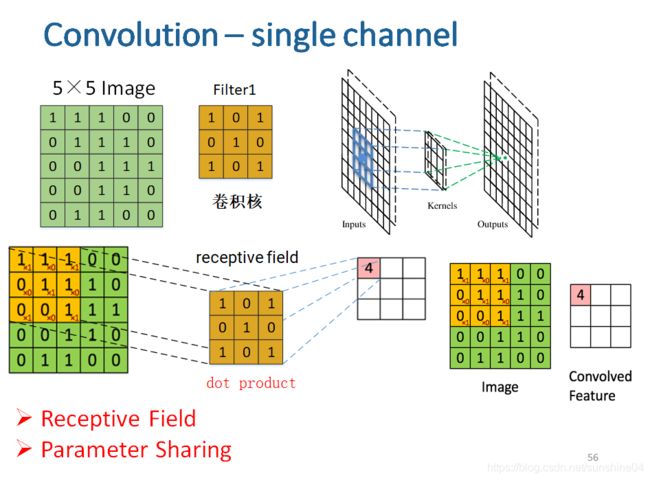
(1)Receptive Field(局部感受野)
每个隐层节点只连接到图像某个局部的像素区域,从而大大减少需要训练的权值参数。
(2)Parameter Sharing(权值共享)
(3)Pooling(Subsampling) (池化)
降维
2、典型的CNN结构
(1)输入层
保持image最原始的像素值,
input是一个向量,这里是一个多通道(RGB)的image
[width x height x channels ] = (here) [32 × 32 × 3]
(2)Convolution – single channel(单通道)
卷积核:权值w(权值共享)
有点像提取特征的意味
N × N Image F×F Filter -----> Output size = (N - F) / S + 1 Feature Map
Stride (S):步长
Trainable Parameters:The value in filter (Weights)
需要训练的参数:卷积核(是随机初始化的,所以需要学习)
问题:输出是小数
防止 Output size 出现小数, 输入通道外围要补0
外围加几圈0? 这是人工需要确定的参数,是一个超参。
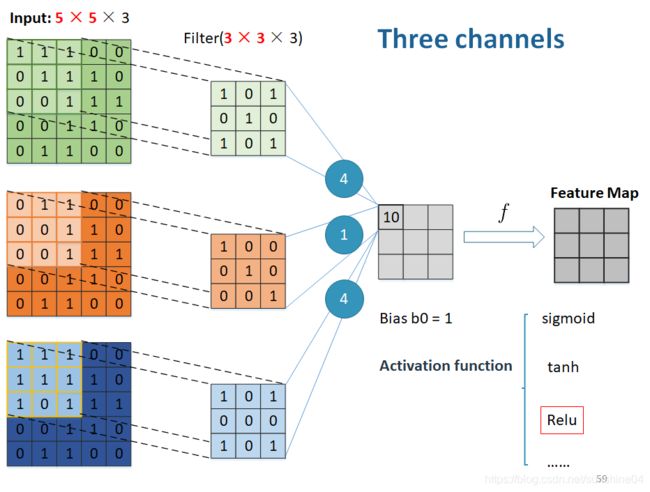
(3)Convolution – Three channel(三通道)
三个卷积求和 + bias(偏置)= 4+1+4+1 = 10
通过激活函数---->得到经过激活的Feature Map
(4)Activation Function(激活函数)
1)sigmoid
饱和时,梯度为0 ,梯度消失,学习参数就不怎么变了。
2)tanh(x)
sigmoid的改进,压缩到[-1 , 1]
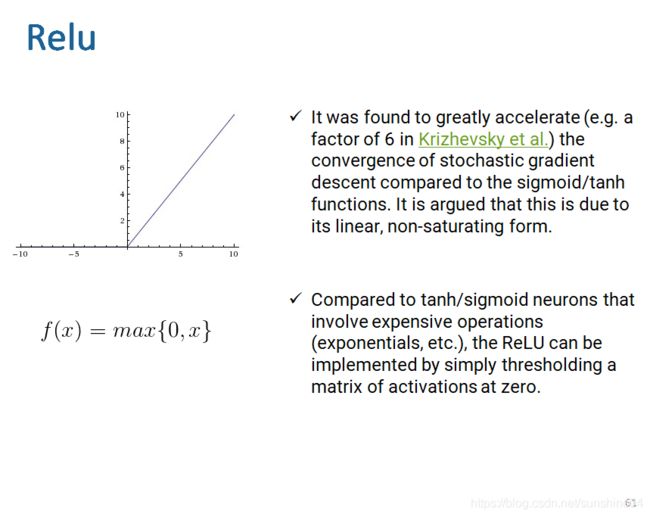
3)relu
比较好的激活函数,没有饱和区域,不会有梯度为0的情况,加快收敛。
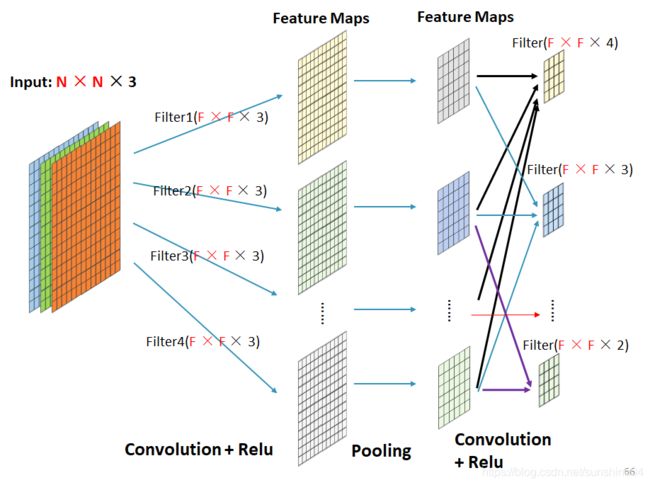
可以 (使用多个卷积核) 提取多组特征,形成多组Feature Map。
CNN中每一层的由多个map组成,每个map由多个神经单元组成,同一个map的所有神经单元共用一个卷积核(即权重),卷积核往往代表一个特征。
每一个Feature Map有一个bias, M个就有M个bias需要学习。
多了一个超参:M(卷积核的数目)
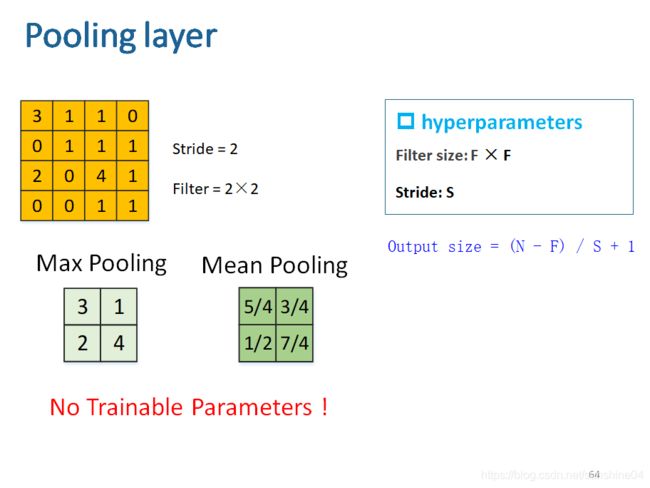
(5)Pooling layer (池化层)
缩小图片规模
最大池化:选某一区域的最大值
均值池化:选某一区域的平均值
无学习参数!!!无w和b
池化:对一个Feature Map进行池化
池化层----->卷积层
池化层好多Feature Map,每一个相当于一个卷积层的输入通道
假设一共四个输入通道,一个卷积核可能只用了其中3个,另一个卷积核可能只用了其中2个
卷积完了再池化
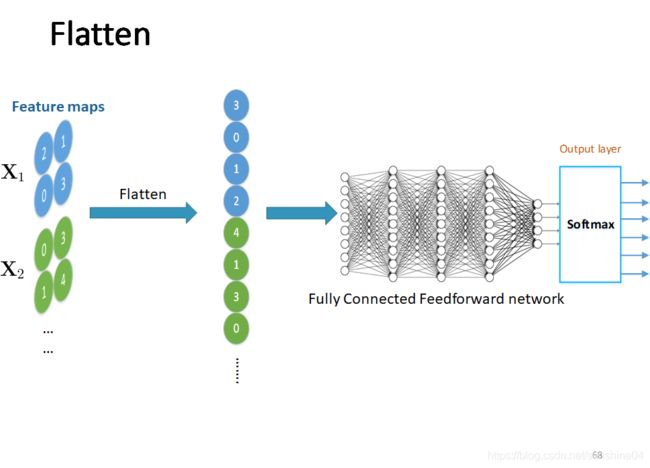
池化之后如果接全连接层,那么需要展开Flatten经过池化的Feature Map
再放入后面的全连接层
总结:
卷积层:深度 = Feature Map 的数量 (可能大于 通道数量吧???) (或者通道数量)
池化层:深度和卷积层一样 因为池化只是需要对每一个 Feature Map 进行池化
全连接层:
(softmax层)
3、手写数字识别
32个Feature Map
卷积核大小 3 × 3
激活函数 relu
最大池化 2 × 2
Dropout : 防止过拟合,训练时选择性忽略一些神经元0.25的概率
Dense 全连接 128个神经元
num_classes:类别数目
编译:
loss 前面用均值平方差,更多用交叉熵
优化:Adadelta,学习率是动态学习的,核心还是梯度下降
度量方式:精度
(三)实训平台内容
1、卷积神经网络
卷积:分为窄卷积、全卷积、同卷积
窄卷积
窄卷积(valid卷积),从字面上也可以很容易理解,即生成的feature map比原来的原始图片小,它的步长是可变的。假如滑动步长为S,原始图片的维度为N1×N1,那么卷积核的大小为N2×N2,卷积后的图像大小(N1-N2)/S+1×(N1-N2)/S+1。
同卷积
同卷积(same卷积),代表的意思是卷积后的图片尺寸与原始图片的尺寸一样大,同卷积的步长是固定的,滑动步长为1。一般操作时都要使用padding技术(外围补一圈0,以确保生成的尺寸不变)。
全卷积
全卷积(full卷积),也叫反卷积,就是把原始图片里的每个像素点都用卷积操作展开。如图所示,白色的块是原始图片,浅色的是卷积核,深色的是正在卷积操作的像素点。反卷积操作的过程中,同样需要对原有图片进行padding操作,生成的结果会比原有的图片尺寸大。
全卷积的步长也是固定的,滑动步长为1,假如原始图片的维度为N1×N1,那么卷积核的大小为N2×N2,卷积后的图像大小,即N1+N2-1×N1+N2-1
前面的窄卷积和同卷积都是卷积网络里常用的技术,然而全卷积(full卷积)却相反,它更多地用在反卷积网络中,关于反卷积网络的内容,将在后面的章节进行介绍。
反卷积神经网络
1反卷积是指,通过测量输出和已知输入重构未知输入的过程。在神经网络中,反卷积过程并不具备学习的能力,仅仅是用于可视化一个已经训练好的卷积网络模型,没有学习训练的过程。
注意:tf.nn.max_pool_with_argmax的方法只支持GPU操作,所以利用这个方法目前还不能在CPU机器上使用。
深度学习中的Epoch,Batchsize,Iterations,都是什么鬼?深度学习中的Epoch,Batchsize,Iterations,都是什么鬼?