图形学学习笔记2——点阵图形光栅化

点阵图形光栅化

将参数描述的图形转化为点阵的算法，评价指标有：精度、时间复杂度、空间复杂度。对实时性要求高的实时渲染场景比如游戏动画，应该需要更快的转化为点阵。类似制作动画片的离线渲染就对精度要求更高。

---

线条图形转化要求

• 线段端点准确
• 线段亮度均匀
• 算法速度快

直线光栅化算法

数值微分发（DDA）

DDA（Digital Differential Analyzer）基本思想使用直线的微分基本方程，从起始点向结束点前进，利用微分方程求出递推式，保证每次求出的点和前一个点相邻。

{xi+1¯¯¯¯¯¯yi+1¯¯¯¯¯¯=xi¯¯¯=yi¯¯¯ororxi+1¯¯¯¯¯¯yi+1¯¯¯¯¯¯=xi¯¯¯+1=yi¯¯¯+1

直线差分方程

kxi+1yi+1=dydx=xi+δx=yi+δy(1)(2)(3)

给定线段两点 p1 , p2 ，选取长边的步长作为一个像素，根据斜率计算另一边的步长。即：如果 |p1.x−p2.x|>=|p1.y−p2.y| ，则选取x方向为单位步长方向，否则选取y方向。

{δx=1δx=1/kδy=k0<|k|≤1δy=11<|k|

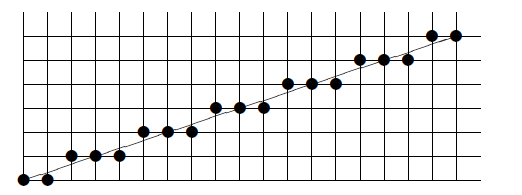
直线光栅化效果:

Bresenham直线算法

Wikipedia:Bresenham line algorithm

思想还是DDA，简化运算量。
当 0<k<1 时， xi¯¯¯ 每次增加1， yi¯¯¯ 每次增加0或1.因此只要判别 yi¯¯¯ 每次增量即可。
判别式是 y(xi) 分别到 yi¯¯¯+1 和 yi¯¯¯ 的距离差值，判别式大于0,离 yi¯¯¯+1 更近，则增量为1，否则0。
直线 y=kx+b ,假设 (0<k<1)

{d1d2=yi¯¯¯+1−k(xi¯¯¯+1)−b=k(xi¯¯¯+1)+b−yi¯¯¯

判别式

d1−d2pi=Δx∗(d1−d2)=2yi¯¯¯−2k(xi¯¯¯+1)−2b+1=2Δx∗yi¯¯¯−2Δy∗xi¯¯¯−(2k+2b−1)∗Δx

可以求得判别式的递推式

pi+1=pi+2Δy−2Δx⋅(yi+1¯¯¯¯¯¯−yi¯¯¯)

假设初始端点和结束端点都是整数点，则 y1¯¯¯=k(x1¯¯¯¯)+b , Δx 和 ΔY 均为整数。有：

p1xi+1=2Δy−Δx=xi+1

{yi+1pi+1=yi+1=pi+2(Δy−Δx)pi≥0

{yi+1pi+1=yi=pi+2Δypi<0

• 从上式可以看出，推导过程只涉及整数加减法和2的乘（移位操作），计算简单容易硬件实现。

圆的光栅化算法

根据圆的对称性，只用计算 θ∈[π/4,π/2] 圆弧即可。

一般方法

lθ 圆弧坐标

y=R2−x2−−−−−−−√x∈[0,R/2√]

在这一段圆弧上斜率 |k|<1 ，所以每次x步长增加1，由上式计算出相应的y。由于涉及到开方和乘法，效率很低。

折线逼近法

一段圆弧 [ts,te] 用n段折线逼近，每段折线对应弧度 δ=(ts−te)/n 。
最大误差：

ϵ=R(1−cos(δ/2))

令 ti=ts+i⋅δ ，假设圆心在原点，则有

xi+1=cos(ti+1)=xicos(δ)−yisin(δ)yi+1=sin(ti+1)=yicos(δ)+xisin(δ)

推导式中 cos(δ) 和 sin(δ) 是常数，只涉及到乘法和加法，效率更高。计算出折线端点后，找到最近的整数点得到 (xi¯¯¯,yi¯¯¯) ，再用直线算法绘制端点之间的部分。
不过随着迭代次数的增加，累计误差也会增大。

Bresenham 圆的算法

wikipedia: Bresenham’s circle algorithm
与Bresenham直线算法的思想一致，都是通过判定判别式来确定推导式的步长。

考虑圆心在原点的圆，根据对称性，只考虑 [π/4,π/2] 的圆弧， x∈[0,R/2√] 。这段圆弧上斜率 0≤|k|≤1 ，因此 xi¯¯¯ 步长为1， yi¯¯¯ 随着 x 增加，步长为0或-1。
在这段圆弧上:

xi=xi¯¯¯=i

yi+1¯¯¯¯¯¯ 的值取决于 yi+1 能被 yi¯¯¯ 与 y1¯¯¯−1 哪一个更好的 度量。

• 此处用词度量并没有说距离，是因为在Bresenham算法中是用平方之后的值的差值来比较，并不是距离。

即度量 yi+1 与 yi¯¯¯ 的差距 |yi¯¯¯2−y2i+1| , yi+1 与 yi¯¯¯−1 的差距 |yi¯¯¯2−(yi+1−1)2|

定义判别式

pi=|y2i+1−yi¯¯¯2|−|y2i+1−(yi¯¯¯+1)2|

最终可化为

pi+1={pi+4xi+6pi+4xi+10(pi<0)(pi≥0)

• 仍然只涉及到整数的加减法和移位操作。简单，效率高。

椭圆算法

算法思想和圆类似。考虑标准椭圆模型，根据对称性，只用计算第一象限的点，设 x∈[0,a] 。

• 为了保证点的连续性，随着 x 从 0 开始增大， |k| 逐渐从 0 变为 +∞ 。
• 当|k|<1时，x步长每次增加1。 当|k|>1时，y每次的步长增加1。

因此，我们先计算 |k|=1 时，在第一象限中 x 的值 xc 。

• 在 x∈[0,xc] 中，可使用圆中的Bresenham同样的思想，求出判别式推导公式。
• 在 x∈[xc,a] 中，以y为步长1，计算x步长变化的判别式，推导思路相同。

---

该系列学习笔记主要参考 郑州师范大学 柳朝阳的《计算机图形学的概念与方法》，如需要查阅更详细的公式推导，可参考原著。