Python数据结构与算法 DAY 01 引入概念&顺序表&链表
Python数据结构与算法 DAY 01 引入概念&顺序表&链表
一 数据结构与算法引入概念
学到至今我们对python的程序已经有了一定的认识 从现在开始我们需要继续跟深入了解 那么我们不只能局限于将一个程序写出来能运行即可 我们还需要研究使用什么样的方法才能让程序更加简洁 同等条件下计算的时间更小 程序的可读性更强
(首次尝试)
首先我们先看一个例题:
如果 a + b + c = 1000 , 且 a^2 + b^2 = c^2
(a,b,c都为自然数),
如何求出所有a,b,c可能的组合
首先我们肯定想到的是for循环嵌套 最简单想到的方法就是
for a in range(1001):
for b in range(1001):
for c in range(1001):
if a+b+c == 1000 and a**2 + b**2 == c**2:
print('a,b,c',a,b,c)
通过for循环嵌套 分别遍历a b c 三个部分 当然 不可否认 这样的确可以获得正确答案 但是我们做了很多不需要做的部分 比如 a或者b的值不可能大于500 又比如c实际上可以表示为1000-a-b 这样就可以省掉c的又一轮遍历 这样三层循环光是循环就需要循环1000**3次 并且还需要判断相同次数 无疑对计算机来说 这是一个十分巨大的工程
小编在运行这个程序的时候 使用了125秒
二 算法的提出
- 算法的概念
算法是计算机处理信息的本质 因为计算机程序本质上是一个算法来告诉计算机确切的步骤来执行一个指定的任务 一般的 当算法处理信息时 会从输入设备或者数据的地址读取数据 把结果写入输出设备或者某个储存地址供以后在调用
tips: 算法是独立存在的一种解决问题的方法和思想
对于算法而言 实现的语言并不重要 重要的是思想
算法可以有不同的语言描述实现版本(如C描述,C++描述,python描述等) , 我们现在使用的是python语言进行描述实现 - 算法的五大特征
- 输入 : 算法具有0个或者多个输入
- 输出 : 算法至少有1个或者多个输出
- 有穷性 : 算法在有限的步骤之后会自动结束而不会无限循环 并且每一个步骤可以在接受的时间内完成
- 确定性 : 算法中的每一步都有确定的含义 不会出现二义性
- 可行性 : 算法的每一步都是可行的 也就是说每一步都能够执行有限的次数完成
三 第二次尝试
import time
t_start = time.time()
for a in range(1001):
for b in range(1001-a):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print('a,b,c',a,b,c)
t_end = time.time()
print(t_end - t_start)
这个程序通过优化之后 只是用了两个循环 并且由于优化了b的循环此时 所以本程序运行完毕 得到与第一次尝试时的程序相同的结果 只需要0.1秒 这就是优化算法的魅力
四 算法效率的衡量
- 执行时间反应算法效率
对于同一个问题 我们给出了两种解决算法 在两种算法的实现中 两端程序执行的时间相差悬殊 由此我们可以得出:
实现算法程序的执行时间可以翻译出算法的效率 即算法的优劣 - 单靠时间值绝对可信吗
单纯依靠运行时间来比较算法的优劣并不一定是客观准确的
所以我们需要引入时间复杂度 ‘大O记法’ - 时间复杂度与 ‘大O记法’
- 时间复杂度的几条基本计算规则
- 基本操作 即只有常数项 时间复杂度为O(1)
- 顺序结构 时间复杂度按照加法进行计算
- 循环结构 时间复杂度按照乘法进行计算
- 分支结构 时间复杂度取最大值
- 判断一个算法效率时 往往只需要关注操作数量的最高次项,其他次要项和常数项可以忽略
- 没有特殊说明时 我们分析算法的时间复杂度都是指的是最坏时间复杂度
- 时间复杂度的几条基本计算规则
五 常见的时间复杂度
六 python的内置类型性能分析
- timeit模块
timeit模块可以用来测试一小段python代码的执行速度 - class(number = 1000000)
Timer类中测试语句执行速度的对象方法 number参数测试代码时的测试次数 默认为1000000此 方法返回的代码平均耗时 一个float类型的秒数 - 对list增加操作的操作测试
def test1():
l = []
for i in range(1000):
l = l + [i]
def test2():
l = []
for i in range(1000):
l.append(i)
def test3():
l = [i for i in range(1000)]
def test4():
l = list(range(1000))
from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "seconds")
# ('concat ', 1.7890608310699463, 'seconds')
# ('append ', 0.13796091079711914, 'seconds')
# ('comprehension ', 0.05671119689941406, 'seconds')
# ('list range ', 0.014147043228149414, 'seconds')
从这个可以看出 创建列表最快速的方法为list(range) 在列表后方插入的时间会比再前方插入的时间短
- 对list的pop操作测试
x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")
# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')
七 数据结构
- 概念
数据是一个抽象的概念 将其进行分类后得到程序设计语言中的基本类型 如 int float char等 属于元素之间不是独立的 而是存在特定的关系 这些关系便是结构 数据结构指数据对象中数据元素之间的关系
python给我们提供了很多现成的数据结构 这些是系统定义好的 不需要我们自己取定义的数据结构叫做python的内置数据结构 比如说列表 元组 字典 而有些数据结构组织方式python系统里面没有定义 需要我们自己取定义实现这些数据组织方式 这些数据组织方式称之为python的拓展数字结构 比如栈 队列 - 算法和数据结构的区别
数据结构只是静态的描述了数据元素之间的关系
高效的程序需要再数据结构的基础上涉及和选择算法
程序 = 数据结构 + 算法
总结 : 算法是为了解决实际问题而设计的 数据结构是算法需要处理的问题载体 - 抽象数据结构类型(Abstract Data Type)
最常用的数据运算的五种:
插入
修改
删除
查找
排序
八 顺序表
- 顺序表在内存中的储存
顺序表数据本身连续储存 每个元素所占的储存单元大小固定相同 元素下标是其逻辑地址 ,而元素的物理地址(实际内存地址)可以通过储存区的起始地址loc(e0)加上逻辑地址(第i个元素)与储存大小成绩计算得
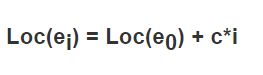
访问指定的元素无需从头遍历 通过计算便可获得对应的地址 其时间复杂度为O(1)

tips: 整型在内存中的储存一般为4个字节 如果本身储存的并不是整型 则会通过元素外置的方法 即在内存的另外一个地方开辟一片新的内存存储这个数据 而原来的位置储存的则是这个新开辟地方的内存地址 这这就叫元素外置方式 列表也是使用这样的方法
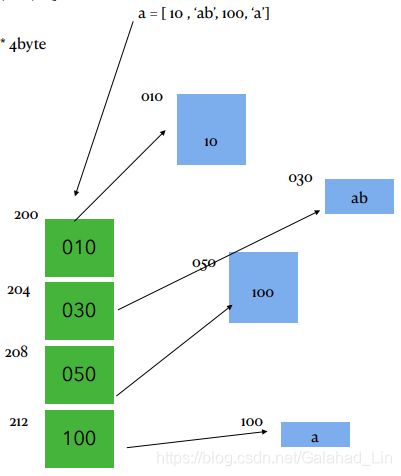
- 顺序表的结构与两种基本实现方式
一个顺序表的完整信息包括两个部分 一部分是表中元素的集合 另一部分是为实现正确操作而需记录的信息 即有关表的整体情况信息 这部分信息主要包括元素储存区的容量和当前表中已有的元素个数两项- 一体式结构
即储存表信息的单元与元素储存区以连续的方式安排在一块储存区中 两部分数据的整体形成一个完整的顺序表对象
一体式结构整体性强 易于管理 但是由于数据元素储存区域是表对象的一部分 顺序表创建以后 元素储存区就固定了
tips: 使用这种数据结构的最大的问题是 如果达到储存的上线 系统会在内存中的另外一个地方重新划一块更大的区域 并将当前的结构赋值给新的区域 并且销毁原来这个小的区域 那么创建新的区域以及销毁原来的区域会使用很多的资源 也会导致运行速度更慢
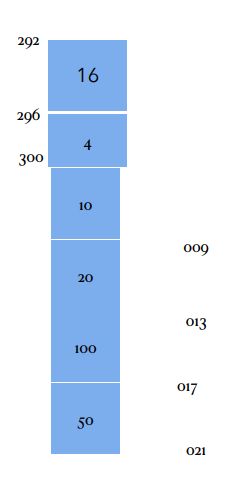
- 分离式结构
分离式结构 表对象里只保存与整个表有关的信息(即容量和元素个数),实际数据元素存放在另一个独立的元素存储区里 通过连接与基本表对象关联

- 一体式结构
- 元素储存区替换
- 一体式结构由于顺序表信息区与数据区连续储存在一起 所以如果想要更换数据区 则只能整体搬迁 及整个顺序表对象(存储顺序表的结构信息区域)改变了
- 分离式结构若想更换数据区 只需要将表信息中的数据区连接地址跟新就可以了 而该顺序表对象不用变
- 扩充的两种策略
- 每次扩充增加固定数目的储存位置 如每次扩充增加10个元素位置 这种策略可称为线性增长
特点: 节省空间 但是扩充操作频繁 操作次数多 - 每次扩充容量加倍 如每次扩充增加一倍的储存空间
特点: 减少了扩充操作的执行次数 但是可能浪费空间资源 以空间换时间 推荐的方式
- 每次扩充增加固定数目的储存位置 如每次扩充增加10个元素位置 这种策略可称为线性增长
九 顺序表的操作(增加和删除元素)
- 增加元素
a. 尾端加入元素 时间复杂度为O(1)

b. 非保序的加入元素(并不常见) , 时间复杂度为O(1)
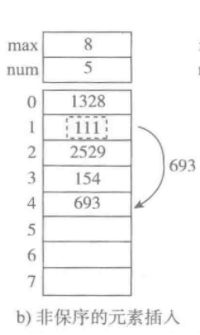
c. 保序元素加入 时间复杂度为O(n)
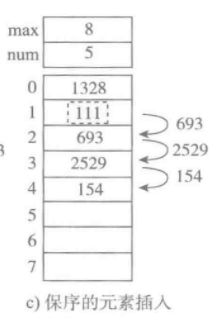
- 删除元素
a. 删除表尾的元素 时间复杂度为O(1)

b. 非保序的元素删除(不常见) 时间复杂度为O(1)

c. 保序元素删除 时间复杂度为O(n)

十 链表
- 使用链表的原因
顺序表的构建需要预先知道数据大小来申请连续的储存空间,而在进行扩充时有需要进行数据的搬迁 所以使用起来并不是特别灵活
链表结构可以充分利用计算机内存 实现灵活的内存动态管理 - 链表的意义
链表是一种常见的数据结构 是一种线性表 但是不想顺序表一样连续储存数据 而是在每一个节点(数据储存单元里)存放下一个节点的位置信息(内存地址)

十一 单项链表
单项链表也叫做单链表 是链表中最简单的一种形式 它的每一个节点包含两个域 一个信息域(元素域)和一个连接域 这个连接指向链表中的下一个节点 而最后一个节点的连接域则为指向一个空值(None)
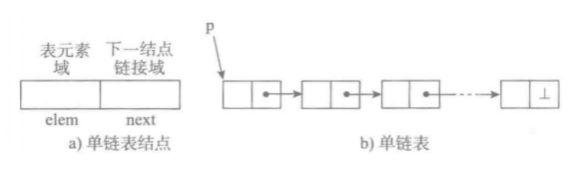
- 节点的创建实现
class Single(object):
def __init__(self,item):
self.item =item
self.next = None
- 单链表的增删改查操作的实现
class Method(object):
# 创建初始值 将代表链首个节点的__head 定义并设置为None 即默认该链没有长度 也没有节点
def __init__(self):
self.__head = None
# 判断 : 该链是否为空
def is_empty(self):
if self.__head == None:
return True
return False
# 链的长度判断:
# 这是其中一种判断方法 这种判断方法的优势在于 不会需要判断该链中是否有节点 因为如果本身是空链 是无法进入循环的 并且number的默认值为0
def length(self):
# 创建一个计数器 用于记录链的数量
number = 0
# 创建一个指针 首先指向链的第一个节点
cur = self.__head
# 创建一个循环 将这个循环从第一个节点进行到最后一个节点 (判断是否为最后一个节点的方法为判断 cur.next是否等于None)
while cur.next != None:
cur = cur.next
number += 1
return number
# 增: 在链的最前端进行插入
def insert_top(self,item):
# 首先创造新的节点(使用Single类创建一个对象) 包含 item 和 next
single = Single(item)
# 将对象的next指向目前第一个节点 因为目前__head的已经指向了第一个节点 所以我们只需要和head指向的内容相同即可
single.next = self.__head
# 将head的指向转向新的节点
self.__head = single
# 增: 在链的末尾增加
def insert_end(self,item):
# 首先先创建一个新的节点(使用Single类创建一个对象) 包含item 和 next
single = Single(item)
# 由于是加在最后的 所以我们需要定义一个指针 并且让指针指向目前的最后一个
cur = self.__head
# 使用循环实现将指针指向最后目前最后一个节点
while cur.next != None:
# 将指针一次一次向后移动 移动到cur.next == None 为止
cur = cur.next
# 目前cur指针已经指向目前链的最后一个节点了 那么就将最后一个节点的next指向新创建的新节点即可(由于新节点的next默认为None 所以不需要重新设置)
cur.next = single
# 增: 输入插入的位置 在指定的位置插入新的节点 类似于列表内的insert的效果
def insert_middle(self,indexs,item):
'''
:param indexs: 输入插入的索引 类型为整型int
:param item: 插入的值 (用于创建新节点的对象)
:return: None
'''
# 首先先创建一个新的节点
single = Single(item)
# 判断是否为空链
if self.is_empty() == False:
# 判断是否为输入的索引为开头
if indexs<=0:
self.insert_top(item)
# 判断是否输入的索引为末尾
elif indexs >= (self.length()-1):
self.insert_end(item)
# 如果插入的位置是在中间
else:
# 创建一个指针 初始值为指向链的第一个节点
cur = self.__head
# 创建一个计数器 目的是判断指针是否移动到需要插入的位置的前一个节点
count = 0
# 写入循环 逻辑是只要计数器(反应的是当前指针指向的索引位置)
while count < (indexs-1):
cur = cur.next
count += 1
# 将新的节点指向目前当前位置之后的节点
single.next = cur.next
# 将目前的节点的next指向新创建的节点
cur.next = single
else:
print('本链为空 默认插入的索引为0')
self.insert_top(item)
# 删除 : 删除其中一个元素
def _delete(self,indexs):
'''
:param indexs: 需要删除的元素的索引
:return:
'''
# 判断该链是否为空链
if self.is_empty() == False:
# 创建游标cur
cur = self.__head
# 创建新游标 precur 这个游标的进度会比cur慢一个单位 也就是指向的是cur上一个节点
precur = None
# 判断输入的indexs是否为链的首个
if indexs <= 0:
self.__head = cur.next
cur.next = None
# 判断输入的indexs是否为链的末尾
elif indexs >= (self.length() - 1):
# 这里写判断条件 目的是 经过循环之后 输出的cur指向的是最后一个节点 而pre指向的是倒数第二个节点
while cur.next != None:
precur = cur
cur = cur.next
# 变换指向 将需要删除目标的上一个节点的next 指向 None
precur.next = None
# 若输入的indexs是否为链的中间
else:
# 设置计数器 计数器反应的部分即为cur的索引
count = 0
# 设置循环 设置判断条件 让循环结束后 cur指向需要删除的目标索引节点 precur指向删除目标节点上一个节点
while count < indexs:
precur = cur
cur = cur.next
count += 1
# 变换指向 将需要删除目标的上一个节点的next 指向 需要删除目标后面的节点
precur.next = cur.next
# 将需要删除目标的next设置为None
cur.next = None
else:
print('error,该链为空')
# 查找该节点是否存在
def seaching(self,item):
# 设置指针 并默认指向head
cur = self.__head
# 设置循环 循环判断指向的节点的item值和输入的item值是否相同 相同则输出True 并且停止循环
while cur != None:
if cur.item != item:
return True
else:
cur = cur.next
# 如果遍历结束没有找到 则返回False
else:
return False
# 遍历链
def travel(self):
# 创建指针
cur = self.__head
while cur != None:
print(cur.item,end=' ')
cur = cur.next
else:
print()
- 测试该单链表
if __name__ == "__main__":
ll = Method()
ll.insert_top(1)
ll.insert_top(2)
ll.insert_end(3)
ll.insert_middle(2, 4)
print ("length:",ll.length())
ll.travel()
print( ll.seaching(3))
print (ll.seaching(5))
ll._delete(1)
print ("length:",ll.length())
ll.travel()
十一 链表与顺序表的对比
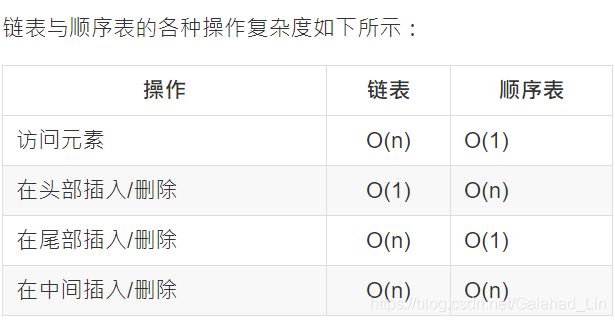
注意虽然表面看起来复杂度都是 O(n),但是链表和顺序表在插入和删除时进行的是完全不同的操作。链表的主要耗时操作是遍历查找,删除和插入操作本身的复杂度是O(1)。顺序表查找很快,主要耗时的操作是拷贝覆盖。因为除了目标元素在尾部的特殊情况,顺序表进行插入和删除时需要对操作点之后的所有元素进行前后移位操作,只能通过拷贝和覆盖的方法进行。