垃圾小肥羊leetcode刷题记录4
我的解法:
class Solution:
def trailingZeroes(self, n: int) -> int:
fives = 0
while n > 0:
n = n//5
fives += n
return fives
末尾的一个零表示阶乘中至少有一对2和5的因子,由于2因子的数量远多于5因子,因此只需考虑阶乘的所有乘数中一共有多少个5因子。需要注意的是有的乘数会包含多个5因子,如25包含两个5因子。因此,我们需要可以通过n/5来统计含有一个5因子的乘数数量,n//25统计含有两个5因子的乘数数量,以此类推,最终得到所有5因子的数量也就是阶乘后0的数量。
我的解法:
class Solution:
def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
carry = 0
dummy_node = ListNode()
curr = dummy_node
while l1 or l2 or (carry > 0):
if (not l1) and l2:
sumi = l2.val+carry
elif (not l2) and l1:
sumi = l1.val+carry
elif (not l1) and (not l2):
sumi = carry
else:
sumi = l1.val+l2.val+carry
carry, rem = sumi//10, sumi%10
curr.next = ListNode(rem)
curr = curr.next
if l1:
l1 = l1.next
if l2:
l2 = l2.next
return dummy_node.next
同时遍历两链表,记录对应元素的和的进位值和余数。若其中一个链表已经为空,则计算另一链表与进位值之和,更新进位值和余数;若两链表均为空,但进位值仍然大于0,则只考虑进位值,再运行一次创建新节点。开始时创建伪头节点,将各新增节点依次链接到尾部。时间复杂度O(n),空间复杂度O(n)。
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if not s:
return 0
hist, t, t_max, i = [], 0, 0, 0
while i < len(s):
if s[i] not in hist:
hist.append(s[i])
t += 1
i += 1
else:
hist = hist[hist.index(s[i])+1:]
t_max = max([t_max, t])
t = len(hist)
return max([t_max, t])
创建队列,遍历字符串,若当前字符不在队列中,则压入队列;若之前存在于队列中,则记录当前最大连续值,同时将之前出现过的当前字符及其之前字符从队列中推出,保证队列长度即为有效连续无重复字符串。时间复杂度O(n2)。
大佬解法:
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
if not s:
return 0
lp, rp, max_, hist= 0, 0, 0, []
while rp < len(s):
if s[rp] not in hist:
hist.append(s[rp])
rp += 1
else:
max_ = max([max_, rp-lp])
lp += 1
hist = hist[1:]
return max([max_, rp-lp])
定义左指针指向开始的元素,从第一个元素开始,右指针向后遍历寻找最长无重复子窜,用列表hist记录出现过的所有字符,记录当前最长子串数。左指针右移一格,删除hist中的第一个元素,右指针继续向后遍历,重复操作至右指针指向字符串尾部。时间复杂度O(n)。
大佬解法:
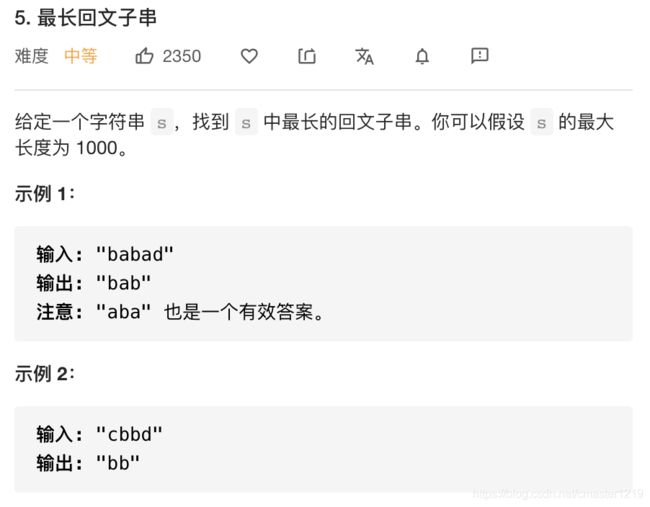
class Solution:
def longestPalindrome(self, s: str) -> str:
n, ans= len(s), ""
dp = [[False]*n for _ in range(n)]
for l in range(n):
for i in range(n):
j = i + l
if j == n:
break
if l == 0:
dp[i][j] = True
elif l == 1:
dp[i][j] = s[i] == s[j]
else:
dp[i][j] = dp[i+1][j-1] and s[i] == s[j]
if dp[i][j] and l+1>len(ans):
ans = s[i:i+l+1]
return ans
动态规划。定义状态dp[i][j]为字符串s[i:j]是否为回文串。定义l为字符子串的长度,即j=i+l。动态规划边界条件为,dp[i][i]为True;当l为1,即子字符长度为2时,dp[i][j]为两字符是否相等。其他情况下,状态转移条件为,若子字符串两端字符相等,且内部字符串为回文串,则该子字符串也为回文串,即dp[i+1][j-1] == True and s[i] == s[j]。遍历i和l后即可找到相应最长回文子串。时间复杂度O(n2)。
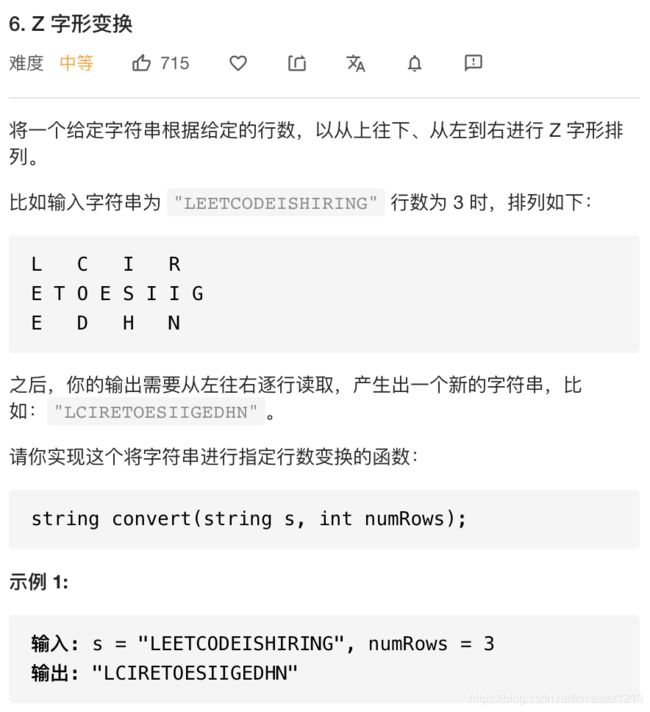
我的解法:
class Solution:
def convert(self, s: str, numRows: int) -> str:
if not s:
return ""
if numRows == 1:
return s
n = len(s)
main, res, add, res2 = n//(2*numRows-2), n%(2*numRows-2), 0, 0
mains = [n*(numRows-1) for n in range(main)]
if res > 0:
add = 1
if res//numRows >=1:
mains.append(main*2)
res2 = res%numRows
matrix = [[""]*(main*(numRows-1)+add+res2) for _ in range(numRows)]
i, row, col = 0, 0, 0
while 1:
while (i < n) and (row < numRows):
matrix[row][col] = s[i]
i += 1
row += 1
row -= 1
while (i < n) and (row > 1):
row -= 1
col += 1
matrix[row][col] = s[i]
i += 1
row -= 1
col += 1
if i == n:
break
ans = ''
for r in range(numRows):
ans += "".join(matrix[r])
return ans
暴力解法,生成目标z字形结构后,将结果逐一读取得到结果。
大佬解法:
class Solution:
def convert(self, s: str, numRows: int) -> str:
n = len(s)
if numRows <= 1:
return s
rows = [""]*numRows
i, r, flag = 0, 0, 1
while i < n:
rows[r] += s[i]
r += flag
i += 1
if r >= numRows-1:
flag = -1
if r == 0:
flag = 1
return "".join(rows)
并不需要真的做出一个题目描述的Z字形数组,关键在于找到字符串各个字母位于的行数。我们发现行数变化的规律为,当触及底部或顶部时,行数变化方向会改变,我们用flag来记录移动方向,1为向下,-1为向上。我们将位于不同行的字符按行数先后组合后即为最终答案。
class Solution:
def myAtoi(self, str_: str) -> int:
str_ = str_.lstrip()
if not str_:
return 0
sign, int_, i = 1, 0, 0
if str_[0] == '-':
sign = -1
str_ = str_[1:]
elif str_[0] == '+':
str_ = str_[1:]
if not str_ or not str_[0].isdigit():
return 0
while i < len(str_):
if str_[i].isdigit():
i += 1
else:
break
int_ = int(str_[:i])*sign
if int_ > 2**31-1:
return 2**31-1
elif int_ < -2**31:
return -2**31
else:
return int_
直接考虑各类特殊情况条件判断,得到最终结果。
大佬解法:
class Solution:
def __init__(self):
self.transfer = {
'start':['start', 'signed', 'number', 'end'], 'signed':['end', 'end', 'number', 'end'],
'number':['end', 'end', 'number', 'end']}
self.start_status = 'start'
# ' ', '+/-', 'number', 'other'
def myAtoi(self, str_: str) -> int:
c, sign, ans = self.start_status, 1, 0
for s in str_:
if s == ' ':
c = self.transfer[c][0]
elif s == '+':
c = self.transfer[c][1]
elif s == '-':
c = self.transfer[c][1]
if c == 'signed':
sign = -1
elif s.isdigit():
c = self.transfer[c][2]
ans = ans*10 + int(s)
else:
c = self.transfer[c][3]
if c == 'end':
break
return min([2**31-1,max([ans*sign, -2**31])])
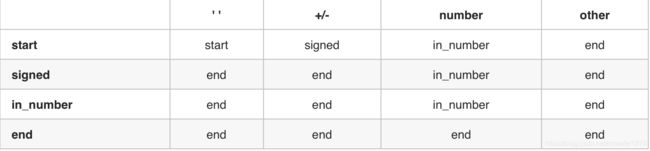
使用自动机方法,定义四个状态以及遇到不同字符后状态的变化方式,如上图所示。遍历字符串,设置初始状态为start,根据遍历到的字符变换状态,同时更新结果,直到状态变为end时,输出结果。
大佬解法:
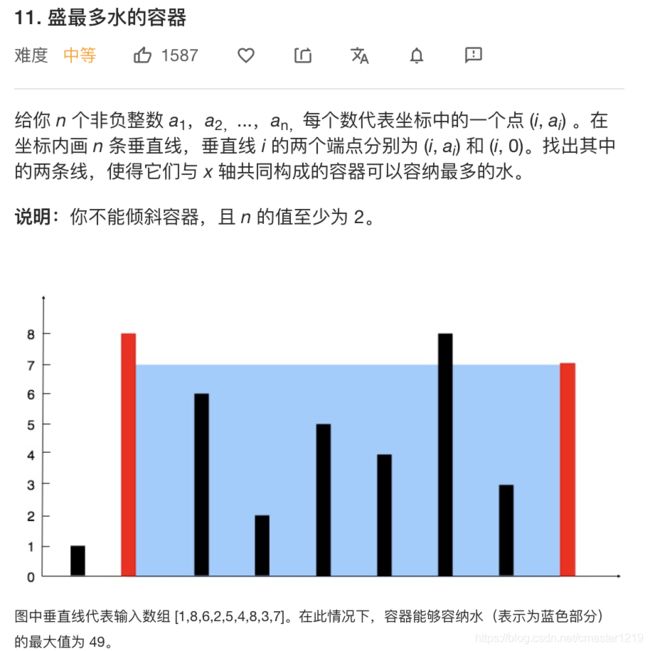
class Solution:
def maxArea(self, height: List[int]) -> int:
def volume(lp, rp):
return (rp-lp) * min([height[rp],height[lp]])
lp, rp, max_ = 0, len(height)-1, 0
while rp > lp:
max_ = max([volume(lp,rp), max_])
if height[lp] >= height[rp]:
rp -= 1
else:
lp += 1
return max_
双指针法,开始时左指针指向列表头部,右指针指向列表尾部,记录当前纳水量。将高度较小的指针向中间方向移动,记录最大纳水量,直到两指针相会。移动高度较小指针是因为若移动高度较大指针,纳水量一定小于不移动时纳水量,移动高度较小指针能考虑其他可能结果。时间复杂度为O(n)。
class Solution:
def intToRoman(self, num: int) -> str:
roms = ['I', 'V', 'X', 'L', 'C', 'D', 'M']
nums = [1, 5, 10, 50, 100, 500, 1000]
ans = ''
while num > 0:
for i in range(6, -1, -2):
ali = num//nums[i]
rem = num%nums[i]
if (ali < 4) & (ali >= 1):
ans += roms[i]*ali
num = rem
elif ali == 4:
ans += (roms[i]+roms[i+1])
num = rem
elif (ali > 4) & (ali < 9):
ans += (roms[i+1]+roms[i]*(ali-5))
num = rem
elif ali == 9:
ans += (roms[i]+roms[i+2])
num = rem
else:
continue
return ans
只考虑十进制数,如1、10、100、1000。将目标数从大到小依次除以这些十进制数,直到整除数大于等于1,根据整除数的大小a在答案中插入相应罗马数字符。若a<4,则插入a个该十进制数对应字符;若a=4,则插入该十进制字符及上一级五进制字符;若4 我的解法: 遍历所有二元组,用字典记录两数和与0的差值,若有多组二元组与0差值相同,用列表的形式储存在同一差值主键下。遍历一遍原数列,判断元素是否在字典的主键集中,若存在完成配对,加入结果集中。最终返回无重复的结果集。时间复杂度O(n2),超过时间限制。 大佬解法: 为避免出现重复,首先将数组排序。用两重循环遍历排序后的数组,因为第一个元素确定后,第二个第三个元素满足特定关系,故可在第二重循环安排首尾双指针,从而省去一重循环。左指针由第二个元素开始,从左向右移动,右指针从最后一个元素开始从右往左移动,若出现满足条件的三个元素,则记录在结果中。第一第二个元素在向后遍历时,必须保证和前一个元素不同,否则会产生重复的结果。时间复杂度O(n2)。 我的解法: 借鉴上一题“三数之和为零”,首先将原数组排序,遍历排序数组作为第一个数,第二第三个数在第一个数之后的数组中利用首尾双指针遍历。计算三数和与目标数之差,若大于0,移动右指针;若小于0,移动左指针;记录最小差值;若等于0,直接返回target。若之前未出现差值为0的情况,则返回目标值与差值的和。时间复杂度O(n2)。 小改进: 借鉴“三数之和为零”,每次移动指针时,保证移动到不同的数。 大佬解法: 回溯算法,将原问题分解为已合成字符串与余下输入数字组合的问题,若无需要输入的数字,则将合成字符加入数组。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
dic, n, ans = {
}, len(nums), []
for i in range(n):
for j in range(i+1, n):
if not dic.get((0-nums[i]-nums[j])):
dic[(0-nums[i]-nums[j])] = [(i,j)]
else:
dic[(0-nums[i]-nums[j])].append((i,j))
for k in range(n):
if dic.get(nums[k]):
for pair in dic.get(nums[k]):
if k in pair:
continue
else:
i, j = pair
new = sorted([nums[i],nums[j],nums[k]])
if new not in ans:
ans.append(new)
return ans
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n, ans = len(nums), []
nums = sorted(nums)
i = 0
while i < n:
j, k = i+1, n-1
while j < k:
if nums[i]+nums[j]+nums[k] < 0:
j += 1
elif nums[i]+nums[j]+nums[k] > 0:
k -= 1
else:
ans.append([nums[i], nums[j], nums[k]])
j += 1
while nums[j] == nums[j-1] and j<k:
j += 1
k -= 1
i += 1
while i<n and nums[i]==nums[i-1]:
i += 1
return ans
class Solution:
def threeSumClosest(self, nums: List[int], target: int) -> int:
n, mindif = len(nums), float(inf)
nums = sorted(nums)
for i in range(n-2):
j, k = i+1, n-1
while j<k:
dif = nums[i]+nums[j]+nums[k]-target
if dif > 0:
k -= 1
elif dif < 0:
j += 1
else:
return target
if abs(dif) < abs(mindif):
mindif = dif
return mindif+target
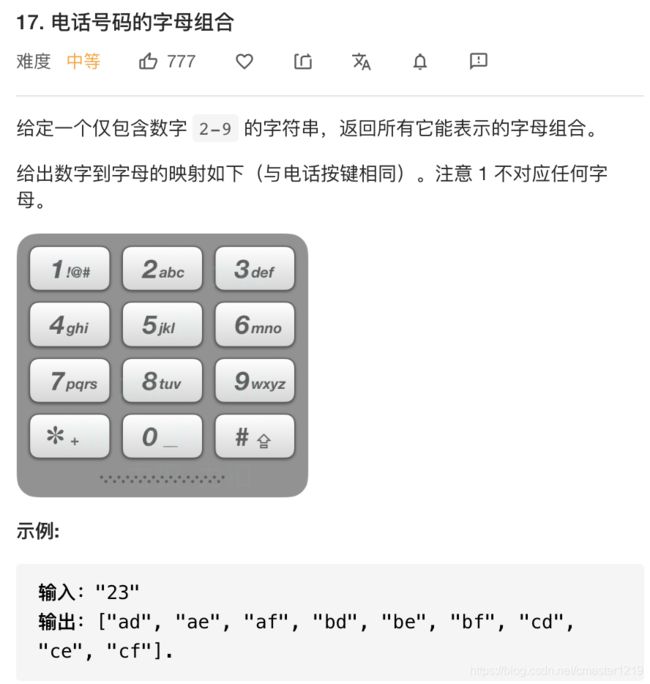
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
dic = {
'2':'abc', '3':'def', '4':'ghi', '5':'jkl', '6':'mno',
'7':'pqrs', '8':'tuv', '9':'wxyz'}
def backtrack(conbination, rest_digits):
if not rest_digits:
ans.append(conbination)
else:
for c in dic[rest_digits[0]]:
backtrack(conbination+c, rest_digits[1:])
ans = []
if digits:
backtrack("", digits)
return ans