【Graph Embedding】DeepWalk:图嵌入的一颗手榴弹
今天学习的是纽约州立大学石溪分校在 NetWork Embedding 的工作《DeepWalk Online Learning of Social Representations》,这篇文章于 2014 年发表于 ACM 会议,目前已经有 2700 多引用,是第一个将 Word2Vec 应用到 NetWork Embedding 并取得了巨大成功的方法。
由于论文比较简单,所以直接进入主题。
1. Introduction
这篇论文提出了一个新的算法——DeepWalk,大致为:通过在网络中随机游走捕获网络局部信息,将游走序列等效为句子利用 Skip-Gram 算法学习 Embedding 向量,从而完成 NetWork Embedding。
通常学习一个 NetWork Embedding 时会关注以下几个性质:
- 适应性:由于网络是动态的,网络表征应能够适应网络的正常演化;
- 社区意识:节点间的编码距离应该能反应出成员之间的社会相似性;
- 低维度:维度低占用内存小,且泛化能力强;
- 连续性:连续的表征不仅可以提供节点的可视化图,也可以在分类时更有健壮性。
作者在应用 Word2Vec 时针对性的提出了一些优化方法使得训练出的 NetWork Embedding 满足了以上需求。
2 DeepWalk
在介绍具体的优化方法之前,我们先来介绍一下随机游走和语言模型相关的知识。
2.1 Random Walks
随机游走是一个随机过程,顾名思义:每次在网络节点中行走时的选择都是随机的,即无法基于过去的行为预测未来的行为。作者采用定长的随机游走作为 DeepWalk 提取局部网络结构的基本工具。
除了提取网络结构外,随机游走还有其它特点:
- 并行化:容易并行化,在网络中可以多放几个 Walker 探索同一个网络的不同区域;
- 局部性:网络发生细微变化时只需重新提取局部网络结构,不需要重新计算全部的网络结构。
2.2 Power Laws
作者选择随机游走来捕获网络结构的原始结构,那如何去从这些结构中提取信息呢?
解决方案大家都知道,是利用 Word2Vec 技术去提取信息,但如何证明其合理性?
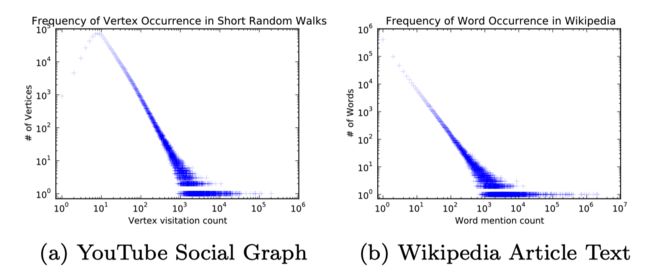
作者将随机游走序列从真实网络中提取到的顶点频率和从维基百科中提取到的单词频率进行对比,发现两者都是服从幂律分布的,如下图所示,这一定程度上说明了两者的相似性,所以 Word2Vec 可以应用于网络结构。
2.3 Language Modeling
简单看下语言模型,给定一个单词序列:
W 1 n = ( w 0 , w 1 , w 2 , . . . , w n ) W_1^n = (w_0, w_1, w_2,...,w_n) \\ W1n=(w0,w1,w2,...,wn)
我们的目标是利用先前的单词去预测下一个单词:
p ( w n ∣ w 0 , w 1 , w 2 , . . . , w n − 1 ) p(w_n|w_0,w_1,w_2,...,w_{n-1}) \\ p(wn∣w0,w1,w2,...,wn−1)
将其扩展到网络图中,以定长随机游走来探索网络结构,并根据先前走过的节点来预测下一个节点 v 的可能性:
p ( v i ∣ ( v 1 , v 2 , . . . , v i − 1 ) ) p(v_i | (v_1,v_2,...,v_{i-1})) \\ p(vi∣(v1,v2,...,vi−1))
这里要注意,我们的目标是获取节点的 Embedding 向量,而不仅仅是求解节点共现概率,所以在这里引入映射矩阵 $\Phi:v \in V \rightarrow R^{ |V| \times d} $ , Φ ( v ) \Phi(v) Φ(v) 代表节点 v 映射后的 d 维向量,有:
p ( v i ∣ ( Φ ( v 1 ) , Φ ( v 2 ) , . . . , Φ ( v i − 1 ) ) ) p(v_i | (\Phi(v_1),\Phi(v_2),...,\Phi(v_{i-1}))) \\ p(vi∣(Φ(v1),Φ(v2),...,Φ(vi−1)))
但随着随机游走的长度增加,概率函数没法计算。这时我们引入 Word2Vec 的 Skip-Gram 算法,利用一个节点来预测周围的节点,于是有:
m i n i m i a z e − l o g ( [ v i − w , . . . , v i − 1 , v i + 1 , . . . , v i + w ] ∣ Φ ( v i ) ) minimiaze \; -log\big( [{v_{i-w},}...,v_{i-1},v_{i+1},...,v_{i+w}] | \Phi(v_i) \big) \\ minimiaze−log([vi−w,...,vi−1,vi+1,...,vi+w]∣Φ(vi))
注:这里的预测是无序性的,不考虑上下文相对给定单词的偏移量, Word2Vec 的顺序无关性也恰好契合随机游走的无序性。
通过将定长随机游走和 Word2Vec 相结合得到了一个满足所有要求的算法,该算法可以生成低维的网络表征,并存在于连续的向量空间中。
2.4 Algorithm
我们来看下算法的具体细节。
下图展示了我们的算法,3-9 行为核心算法:
-
外层循环打乱遍历顶点的顺序(每个节点都会作为随机游走的起点),这样相比于从固定顺序的顶点开始随机游走而言可以加速收敛;
-
内层循环中,我们会遍历序列中的所有的顶点,通过对每个节点进行均匀采样产生定长的随机游走序列,并通过 Skip-Gram 算法完成训练。
这里采用 Skip-Gram 模型利用 Hierarchical Softmax 去优化训练时间,将时间复杂度从 O(|V|) 降低到 O(log|V|),并利用随机梯度下降去优化参数,学习率初始值为 0.025,并随着出现的顶点数量进行线性衰减。
下图总览下 DeepWalk 算法,图 a 为在网络图中进行随机游走并产生序列,图 b 训练 Skip-Gram 模型,并获得输入节点的 Embedding 向量, 图 c 为利用 Hierarchical Softmax 来加速训练。
2.5 Parallelizability
由于网络中随机游走采集到的节点服从幂律分布,所以节点也服从长尾分布(幂律分布的要求高于长尾分布),导致网络层参数的更新比较稀疏(一直更新头部节点)。所以我们采用异步随机梯度下降(ASGD)算法来实现并行化,下图展示了 DeepWalk 并行化的效果:
2.6 Variants
作者还提出了两种算法的变体,一种是改成流式处理,另一种的非随机游走。
2.6.1 Streaming
改成流式处理可以在不了解整个图结构的情况下直接更新模型,但也需要做一些修改:
- 由于没法使用衰减的学习率,所以使用较小的学习率代替;
- 如果预先知道节点的频率,可以继续使用 Huffman 树,否则可以先以最大基数构建树模型,并在发现节点时将其置入空余的叶子结点中。当然,这样构建的肯定不是 Huffman 树,所以会损失一定的训练效率。
2.6.1 Non-Random Walks
根据特定场景可以选择构建非随机游走的序列,这样采集到的图结构不仅可以捕获到网络结构,还可以捕捉到边的频率。一个很实用的场景:网站中的用户导航。这种方法可以在不显示改变模型结构的情况下适应具体的商业场景,并完成特定的商业目的。
3. Conclusions
这篇论文提出的 DeepWalk 打破了 NLP 和网络建模之间的壁垒,在较强的理论基础上将 Skip-Gram 算法应用于 NetWork Embedding 中,扩展了 Embedding 的应用范围,就像扔进 Embedding 领域的一颗手榴弹,将 Embedding 技术推向一个高潮同时也开启了 World Embedding 的时代。
这边我们做一个思考,想下 DeepWalk 有哪些局限性。
DeepWalk 依托随机游走和 Word2Vec,除了具有 Word2Vec 所拥有的局限性外,也包括随机游走带来的局限性。所以 DeepWalk 最大的局限是:只适用于无向图,不适用于有向图。
4. Reference
- 《DeepWalk: Online Learning of Social Representations》
关注公众号跟踪最新内容:阿泽的学习笔记。
![]()