计算机图形学——多边形区域填充算法
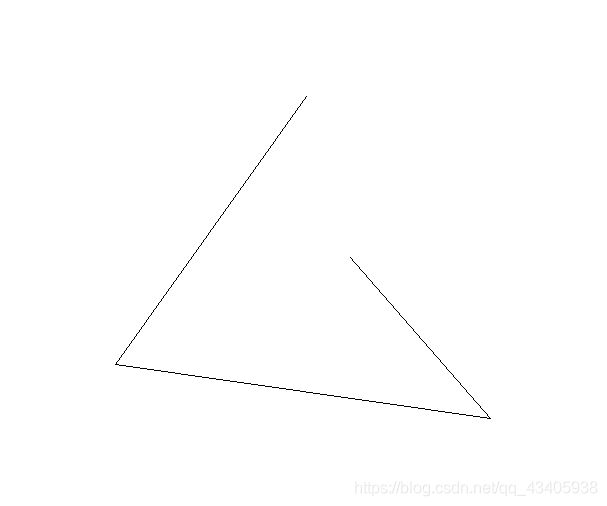
1.橡皮筋效果实现多边形交互输入
环境:使用vs2019提供的MFC框架,在鼠标交互输入中使用橡皮筋算法来实现多边形的输入。首先定义相应变量来保存输入的数据。
int m_pNumbers; //输入点的个数
CPoint m_pAccord[N], m_mousePoint; //保存输入的顶点信息和当前的鼠标所处位置
- 每次进行鼠标点击的时候,便调用OnLButtonDown(UINT nFlags, CPoint
point)函数,若输入的顶点个数不超过规定最大值,便保存当前输入点的信息。 - 在输入第一个点之后,移动鼠标,便会有一条线从上一个输入点A连接到鼠标当前位置,由OnMouseMove(UINT nFlags, CPoint point)函数实现该功能。每次鼠标移动时t1时刻,再一次绘制上一个点A到t1时刻鼠标位置的线段,将该直线隐藏。然后更新m_mousePoint的值,然后绘制当前t2时刻,上一个输入点A到当前t2时刻鼠标位置的线段。
- 在用户输入完成之后,双击完成输入。在这次也是发现了MFC的一个隐藏的知识点,就是在用户双击的时候,MFC会先触发单击事件函数,然后调用双击事件函数,所以这样我们就不用在双击时间函数中去保存双击的输入点信息,只需要将最后的输入点和起点相连即可。
- 以上操作便完成了橡皮筋效果。在完成多边形的绘制之后,便根据用户的选择来进行相应操作。
//橡皮筋效果
void OnLButtonDown(UINT nFlags, CPoint point)
{
// TODO: 在此添加消息处理程序代码和/或调用默认值
if (seedFlag) {
seed_Point = point;
ScanLineFill4(seed_Point.x, seed_Point.y, 0, m_pDC);
seedFlag = false;
}
else if (m_pNumbers < N) {
m_pAccord[m_pNumbers] = point;
m_pNumbers++;
m_mousePoint = point;
}
CView::OnLButtonDown(nFlags, point);
}
void OnLButtonDblClk(UINT nFlags, CPoint point)
{
// TODO: 在此添加消息处理程序代码和/或调用默认值
m_pDC->MoveTo(m_pAccord[m_pNumbers - 1]);
m_pDC->LineTo(m_pAccord[0]);
m_pAccord[m_pNumbers] = m_pAccord[0];
m_pNumbers++;
FillPolyDoc* pDoc = GetDocument();
if (pDoc->m_displayMode == 0 ) {
seedFlag = true;
}
else if (pDoc->m_displayMode == 1) {
Fillpolygon(m_pNumbers, m_pAccord, m_pDC);//有序边表法填充
}
else if (pDoc->m_displayMode == 2) {
PointFillpoly(m_pNumbers, m_pAccord, m_pDC);//逐点法填充
}
else if (pDoc->m_displayMode == 3) {
Triangulation(m_pAccord, m_pNumbers - 1, m_pNumbers - 1);//三角剖分
}
else if (pDoc->m_displayMode == 4) {
Fillpolygon(m_pNumbers, m_pAccord, m_pDC);//图案填充
}
else{
Triangulation(m_pAccord, m_pNumbers - 1, m_pNumbers - 1); //多边形顶点集合,当前多边形顶点数,多边形顶点数
}
m_pNumbers = 0;
CView::OnLButtonDblClk(nFlags, point);
}
void OnMouseMove(UINT nFlags, CPoint point)
{
if (m_pNumbers) {
m_pDC->SetROP2(2);
m_pDC->MoveTo(m_pAccord[m_pNumbers - 1]);
m_pDC->LineTo(m_mousePoint);
m_mousePoint = point;
m_pDC->MoveTo(m_pAccord[m_pNumbers - 1]);
m_pDC->LineTo(m_mousePoint);
}
CView::OnMouseMove(nFlags, point);
}
int OnCreate(LPCREATESTRUCT lpCreateStruct)
{
if (CView::OnCreate(lpCreateStruct) == -1)
return -1;
m_pDC = new CClientDC(this);
return 0;
}
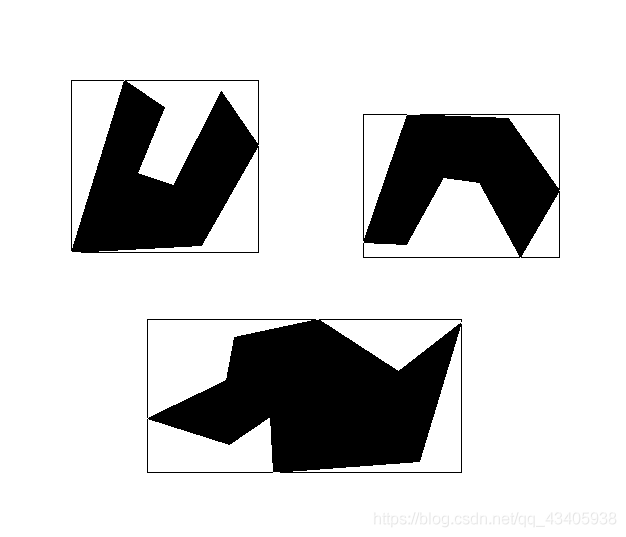
2.逐点法
在逐点法实现中,用到了两个函数。
其中的实现原理十分简单,不过PointInPolygon(int pointNumOfPolygon, CPoint tarPolygon[], CPoint testPoint)函数的实现比较复杂,但这个函数也十分实用,在后面的三角剖分中也有使用。
算法描述:
(1)将给定多边形输入;
(2)求出多边形的最小包含矩形;
(3)逐点扫描最小矩形的每一点,并判断是否位于多边形内部,从最小点到最大点一次判断,如果在该多边形内部,则将该点上色;
(4)判断位于多边形内部的方法是,过每一点水平向右作射线,与多边形边界求交点,如果交点个数为奇数,则说明该点在多边形内部,偶数则说明在多边形外部。
//逐点法填充
void PointFillpoly(int pNumbers, CPoint *points, CDC *pDC)
{
BoxRect_t polyRect;
polyRect = getPolygonRect(pNumbers, points);
m_pDC->MoveTo(polyRect.minX, polyRect.minY);
m_pDC->LineTo(polyRect.minX, polyRect.maxY);
m_pDC->LineTo(polyRect.maxX, polyRect.maxY);
m_pDC->LineTo(polyRect.maxX, polyRect.minY);
m_pDC->LineTo(polyRect.minX, polyRect.minY);
CPoint testPoint;
//从最小点到最大点一次判断,如果在该多边形内部,则进行填充
for (testPoint.x = polyRect.minX; testPoint.x < polyRect.maxX; testPoint.x++)
for (testPoint.y = polyRect.minY; testPoint.y < polyRect.maxY; testPoint.y++) {
if (PointInPolygon(m_pNumbers, m_pAccord, testPoint))
pDC->SetPixel(testPoint.x, testPoint.y, RGB(255, 255, 255));
}
}
//得到该多边形的最大、最小的y、x值
BoxRect_t getPolygonRect(int pointNumOfPolygon, CPoint tarPolygon[])
{
BoxRect_t boxRect;
boxRect.minX = 50000;
boxRect.minY = 50000;
boxRect.maxX = -50000;
boxRect.maxY = -50000;
for (int i = 0; i < pointNumOfPolygon; i++) {
if (tarPolygon[i].x < boxRect.minX) boxRect.minX = tarPolygon[i].x;
if (tarPolygon[i].y < boxRect.minY) boxRect.minY = tarPolygon[i].y;
if (tarPolygon[i].x > boxRect.maxX) boxRect.maxX = tarPolygon[i].x;
if (tarPolygon[i].y > boxRect.maxY) boxRect.maxY = tarPolygon[i].y;
}
return boxRect;
}
//判断点是否位于区域内
BOOL PointInPolygon(int pointNumOfPolygon, CPoint tarPolygon[], CPoint testPoint)
{
if (pointNumOfPolygon < 3)
return false;
bool inSide = FALSE;
float lineSlope, interSectX;
int i = 0, j = pointNumOfPolygon - 1;
for (i = 0; i < pointNumOfPolygon; i++) {
if ((tarPolygon[i].y < testPoint.y && tarPolygon[j].y >= testPoint.y ||
tarPolygon[j].y < testPoint.y && tarPolygon[i].y >= testPoint.y) &&
(tarPolygon[i].x <= testPoint.x || tarPolygon[j].x <= testPoint.x)) {
if (tarPolygon[j].x != tarPolygon[i].x) {
lineSlope = (float)(tarPolygon[j].y - tarPolygon[i].y) / (tarPolygon[j].x - tarPolygon[i].x);
interSectX = (int)(tarPolygon[i].x + (testPoint.y - tarPolygon[i].y) / lineSlope);
}
else
interSectX = tarPolygon[i].x;
if (interSectX < testPoint.x)
inSide = !inSide;
}
j = i;
}
return inSide;
}
3.有序边表法
首先给出有序边表法中定义使用的变量。
int m_Begin, m_End, m_edgeNumbers, m_Scan; //求交边集指针,有效边数,当前扫描位置
float m_yMax[N], m_yMin[N], m_Xa[N], m_Dx[N]; //每条边y最大值,y最小值,每条边与扫描线x的交点,每条边斜率倒数
基本思想:用水平扫描线从上到下(或从下到上)扫描由多条首尾相连的线段构成的多边形,每根扫描线与多边形的某些边产生一系列交点。将这些交点按照x坐标排序,将排序后的点两两成对,作为线段的两个端点,以所填的颜色画水平直线。
- 在实现中首先需要对多边形的每一条边进行处理操作,因为是采用水平线扫描填充,所以对于水平线不做处理。对其余边根据端点的y值大小进行排序,保存yMax,yMin,Xa(相对应的x坐标)以及Dx(斜率的倒数)。
- 在进行扫描的过程中,很重要的一部分操作便是求交边集指针的移动。初始状态位0,在扫描线开始向下移动后,调用Include()函数,检查是否有边进入扫描线交集(即判断所有y最大值大于扫描线当前y值的边线),此时将m_End++,即尾指针向后移动。在Include()函数中,也会调整起始点位置,将Dx调整为位移量。
- 之后调用UpdateXvalue()函数,判断是否有边退出求交边集。
- 如果没有边退出,则移动x,并根据x值大小进行排序。
- 有边退出,更新数组,删除该边,m_Begin++,即头指针向后移动。
- 调用pFillScan(pDC)函数,进行填充。
- m_Scan–,回到第二步进行循环,直到m_Begin==m_End。
算法描述:
- 建立边表的方法:
(1)与x轴平行的边不计入;
(2)多边形的顶点分为两大类:一类是局部极值点,另外一类是非极值点。当扫面线与第一类顶点相交时,应看作两个点;而当扫描线与第二类顶点相交时,应视为一个点,对于极值点则要记录两条边;
(3)扫描线按照y轴从低到高顺次记录;
(4)一条边按照y轴的高低记录;
(5)多条边以x轴递增顺序记录;
- 算法流程:
1、根据给出的多边形顶点坐标,建立NET表,求出顶点坐标中最大y值ymax和最小y值ymin。
2、初始化AET表指针,使它为空。
3、执行下列步骤直至NET和AET都为空.
(1)如NET中的第y类非空,则将其中的所有边取出并插入AET中;
(2)如果有新边插入AET,则对AET中各边排序;
(3)对AET中的边两两配对,(1和2为一对,3和4为一对,…),
将每对边中x坐标按规则取整,获得有效的填充区段,再填充.
(4)将当前扫描线纵坐标y值递值1;
(5)如果AET表中某记录的ymax=yj,则删除该记录 (因为每条边被看作下闭上开的);
(6)对AET中剩下的每一条边的x递增dx,即x’ = x+ dx .
//有序边表法填充
void Fillpolygon(int pNumbers, CPoint* points, CDC* pDC)
{
m_edgeNumbers = 0;
pLoadPolygon(pNumbers, points); // Polygon Loading, calculates every edge's m_yMax[],m_yMin[],m_Xa[],m_Dx[]
//求交边集范围,因为数组已经根据y值大小进行边的排序,所以end向后移动即代表有边进入,start向后移动,代表有边退出
m_Begin = m_End = 0;
m_Scan = (int)m_yMax[0]; //从顶向下扫描
Include(); //检查是否有边进入扫描线
UpdateXvalue(); //检查是否有边退出扫描线
while (m_Begin != m_End) {
pFillScan(pDC);
m_Scan--;
Include();
UpdateXvalue();
}
}
void pLoadPolygon(int pNumbers, CPoint* points)
{
float x1, y1, x2, y2;
x1 = points[0].x; y1 = points[0].y + 0.5;
for (int i = 1; i < pNumbers; i++) {
x2 = points[i].x; y2 = points[i].y + 0.5;
if (abs(int(y2 - y1)) >= 0) //水平线不做处理
{
pInsertLine(x1, y1, x2, y2);
x1 = x2; y1 = y2;
}
else
x2 = x1;
}
}
void pInsertLine(float x1, float y1, float x2, float y2)
{
int i;
float Ymax, Ymin;
Ymax = (y2 > y1) ? y2 : y1;
Ymin = (y2 < y1) ? y2 : y1;
i = m_edgeNumbers;
//根据y值的大小,进行排序插入,大的在前面
while (i != 0 && m_yMax[i - 1] < Ymax) {
m_yMax[i] = m_yMax[i - 1];
m_yMin[i] = m_yMin[i - 1];
m_Xa[i] = m_Xa[i - 1];
m_Dx[i] = m_Dx[i - 1];
i--;
}
m_yMax[i] = Ymax;
m_yMin[i] = Ymin;
if (y2 > y1) m_Xa[i] = x2; //根据y大小确定Xa的值,y大的会先于扫描线相交
else m_Xa[i] = x1;
m_Dx[i] = (x2 - x1) / (y2 - y1); //斜率的倒数
m_edgeNumbers++;
}
void Include()
{
//end向后移动,找出所有边最高点y值大于当前扫描线的边,看是否有新的边进入交集
while (m_End < m_edgeNumbers && m_yMax[m_End] >= m_Scan) {
//有边进入,调整起始点位置,然后将Dx调整为位移量
m_Xa[m_End] = m_Xa[m_End] + (-0.5) * m_Dx[m_End];
m_Dx[m_End] = -m_Dx[m_End];
m_End++;
}
}
void UpdateXvalue()
{
int i, start = m_Begin;
for (i = start; i < m_End; i++) {
if (m_Scan > m_yMin[i]) {
//当前边没有退出,则移动x,然后在进行排序
m_Xa[i] += m_Dx[i];
pXsort(m_Begin, i);
}
else {
//有边退出,更新数组,然后begin++
for (int j = i; j > m_Begin; j--) {
m_yMin[j] = m_yMin[j - 1];
m_Xa[j] = m_Xa[j - 1];
m_Dx[j] = m_Dx[j - 1];
}
m_Begin++;
}
}
}
void pXsort(int Begin, int i)
{
float temp;
while (i > Begin&& m_Xa[i] < m_Xa[i - 1]) {
temp = m_Xa[i]; m_Xa[i] = m_Xa[i - 1]; m_Xa[i - 1] = temp;
temp = m_Dx[i]; m_Dx[i] = m_Dx[i - 1]; m_Dx[i - 1] = temp;
temp = m_yMin[i]; m_yMin[i] = m_yMin[i - 1]; m_yMin[i - 1] = temp;
i--;
}
}
void pFillScan(CDC* pDC)
{
int x, y;
FillPolyDoc* pDoc = GetDocument();
for (int i = m_Begin; i < m_End; i += 2) {
if (pDoc->m_displayMode == 1) {
pDC->MoveTo(m_Xa[i], m_Scan);
pDC->LineTo(m_Xa[i + 1], m_Scan);
}
else if (pDoc->m_displayMode == 4) {
//图案填充
y = m_Scan;
for (int x = m_Xa[i]; x < m_Xa[i + 1]; x++)
if (m_patternData[y % 12][x % 12])
pDC->SetPixel(x, y, RGB(255, 0, 0));
}
}
}
4.图案填充
只需要给出填充的图案,然后存放在二维数组m_patternData中即可,利用取余运算巧妙实现。
//图案
int m_patternData[12][12] = {
{
0,0,0,0,0,1,1,0,0,0,0,0 },
{
0,0,0,0,0,1,1,0,0,0,0,0 },
{
0,0,0,0,0,1,1,0,0,0,0,0 },
{
0,1,1,1,1,1,1,1,1,1,1,1 },
{
0,1,1,0,0,1,1,0,0,1,1,0 },
{
0,1,1,0,0,1,1,0,0,1,1,0 },
{
0,1,1,0,0,1,1,0,0,1,1,0 },
{
0,1,1,1,1,1,1,1,1,1,1,0 },
{
0,0,0,0,0,1,1,0,0,0,0,0 },
{
0,0,0,0,0,1,1,0,0,0,0,0 },
{
0,0,0,0,0,1,1,0,0,0,0,0 },
{
0,0,0,0,0,0,0,0,0,0,0,0 }
};
5.种子填充
点填充有好几种方法,其中比较简单实现的是四连通泛填充算法。基本思路就是给定种子,然后去填充种子上下左右四个方向的像素点,如果为空,则进行填充。
实现代码如下:
void FloodFill4(int x, int y, int fillColor, int oldColor)
{
int current;
current = GetPixel(x,y);
if( current == oldColor ){
SetPixel(x,y,fillColor);
FloodFill4(x+1,y,fillColor,oldColor);
FloodFill4(x-1,y,fillColor,oldColor);
FloodFill4(x,y+1,fillColor,oldColor);
FloodFill4(x,y-1,fillColor,oldColor);
}
}
不过如果运行这一段代码很容易就会导致栈溢出,,,虽然代码简单,但是没法用。
所以更多的是使用扫描线种子填充算法。
算法描述:
- 种子像素入栈。 当栈非空时,重复执行一下操作。
- 栈顶像素出栈。
- 沿扫描线对出栈像素的左右像素进行填充,直到遇到边界像素为止。
- 将上述区间内的最左、最右像素记为 x l e f t x_{left} xleft和 x r i g h t x_{right} xright
- 在区间[ x l e f t x_{left} xleft , x r i g h t x_{right} xright]内检查与当前扫描线相邻的上下两条扫描线是否全为边界像素或已填充的像素,若为非边界和未填充,则把每一区间的最右像素 x r i g h t x_{right} xright作为种子像素压入堆栈,重复执行上述操作。
//扫描线种子填充
int SetRP(int x, int y, COLORREF color, COLORREF mColor, CDC* pDC) {
while (pDC->GetPixel(CPoint(x, y)) == mColor) {
pDC->SetPixel(x, y, color);
x++;
}
return x - 1;
}
int SetLP(int x, int y, COLORREF color, COLORREF mColor, CDC* pDC) {
while (pDC->GetPixel(CPoint(x - 1, y)) == mColor) {
pDC->SetPixel(--x, y, color);
}
return x + 1;
}
void NewLineSeed(std::stack<CPoint>* stk, int lx, int rx, int y, COLORREF color, COLORREF mColor, CDC* pDC) {
int x, e;
for (x = lx + 1, e = rx + 1; x < e; x++) {
//找出每一个区间的最右像素,入栈
if (pDC->GetPixel(CPoint(x, y)) != mColor) {
if (pDC->GetPixel(CPoint(x - 1, y)) == mColor)
stk->push(CPoint(x - 1, y));
}
}
//把rx所在点入栈
if (pDC->GetPixel(CPoint(x - 1, y)) == mColor)
stk->push(CPoint(x - 1, y));
}
void ScanLineFill4(int x, int y, COLORREF color, CDC* pDC)
{
int pRight, pLeft;
std::stack<CPoint> stk;
int mColor = pDC->GetPixel(x, y); //给定种子
stk.push(CPoint(x, y));
while (!stk.empty()) {
CPoint p = stk.top(); //栈顶像素出栈
stk.pop();
pRight = SetRP(p.x, p.y, color, mColor, pDC); //向左向右进行填充
pLeft = SetLP(p.x, p.y, color, mColor, pDC);
//上下两条扫描线处理
NewLineSeed(&stk, pLeft, pRight, p.y + 1, color, mColor, pDC);
NewLineSeed(&stk, pLeft, pRight, p.y - 1, color, mColor, pDC);
}
}
void FloodFill4(int x, int y, int fillColor, int oldColor, CDC* pDC)
{
int current;
current = pDC->GetPixel(x, y);
if (current == oldColor) {
pDC->SetPixel(x, y, fillColor);
FloodFill4(x + 1, y, fillColor, oldColor, pDC);
FloodFill4(x - 1, y, fillColor, oldColor, pDC);
FloodFill4(x, y + 1, fillColor, oldColor, pDC);
FloodFill4(x, y - 1, fillColor, oldColor, pDC);
}
}
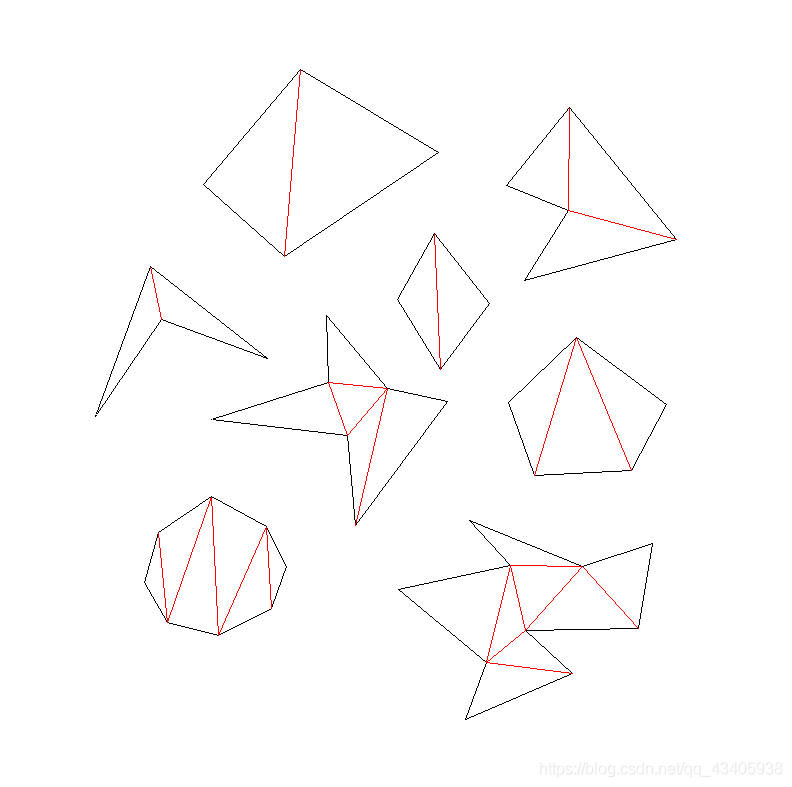
6.多边形三角剖分
关于这个拓展功能的实现,当时在网上看了不少资料,,然后大部分都没有看懂。不过上课的时候老师给了一种使用递归实现的方法,后来发现和网上的耳切法比较相似。
算法描述:
- 选择多边形的最左顶点L+前后顶点,构成一个三角形。
- 检查该三角形内是否有其他顶点。
- 不包含其他顶点。则分割该三角形,递归调用第一步。
- 若包含其他顶点。则连接L与进入的顶点中最左侧的点,这样便会分割该多边形,然后对两个多边形再递归调用第一步。
//多边形三角剖分
void Triangulation(CPoint* points, int pNumbers, int number)
{
if (pNumbers == 3) {
//出口
return;
}
int k, xMin = 100000;
for (int j = 0; j < pNumbers; j++) //找出当前多边形的最左侧顶点
{
if (points[j].x < xMin) {
k = j;
xMin = points[j].x;
}
}
CPoint arry[3];
arry[0] = points[k]; //最左侧顶点
int next = (k + 1) % pNumbers;
arry[1] = points[next]; //后一个顶点
int pre = k - 1;
if (pre < 0)
pre += pNumbers;
arry[2] = points[pre]; //前一个顶点
//围成的该三角形内是否有其他顶点
CPoint in_point[N];
int in_number = 0, i = 0;
xMin = 1000;
for (int j = 0; j < pNumbers; j++)
{
if (j == k || j == next || j == pre) //三角形的三个顶点不算
continue;
if (PointInPolygon(3, arry, points[j])) {
//找出在该三角形内的顶点,并找到其中的最左侧顶点
in_point[in_number] = points[j];
if (in_point[in_number].x < xMin) {
i = j;
xMin = in_point[in_number].x;
}
in_number++;
}
}
if (in_number >= 1) {
//若存在,则链接三角形内的最左侧点,分割多边形,递归调用
CPen pen(PS_SOLID, 1, RGB(255, 0, 0));//创建画笔对象
CClientDC dc(this);
CPen* pOldPen = dc.SelectObject(&pen);
dc.MoveTo(arry[0].x, arry[0].y); //连接线到该最左侧顶点
dc.LineTo(points[i].x, points[i].y);
dc.SelectObject(&pOldPen);
CPoint arry_1[N], arry_2[N]; //分割成两个多边形
int pNumbers_1 = 0, pNumbers_2 = 0;
if (k > i) {
int temp = i; i = k; k = temp;
}
for (int j = 0; j < pNumbers; j++)
{
if (j >= k && j <= i) {
arry_1[pNumbers_1++] = points[j];
}
if (j <= k || j >= i) {
arry_2[pNumbers_2++] = points[j];
}
}
Triangulation(arry_1, pNumbers_1, pNumbers_1);
Triangulation(arry_2, pNumbers_2, pNumbers_2);
}
else {
//若不存在,则分割该三角形,递归调用
CPen pen(PS_SOLID, 1, RGB(255, 0, 0));//创建画笔对象
CClientDC dc(this);
CPen* pOldPen = dc.SelectObject(&pen);
dc.MoveTo(arry[1].x, arry[1].y); //剖分线
dc.LineTo(arry[2].x, arry[2].y);
dc.SelectObject(&pOldPen);
for (int j = k; j < pNumbers - 1; j++) //删除k顶点
{
points[j] = points[j + 1];
}
pNumbers--;
Triangulation(points, pNumbers, number);
}
}
7.MFC画线功能(补充)
关键:
- 鼠标按下时记录初始位置为线的起始端点;
- 利用不同的方法实现画线。下面着重学习总结画线功能实现方法。
在OnLButtonDown函数中记录起始端点,CPoint m_ptOrigin = point;
在OnLButtonUp函数中实现画线。
方法总结如下:
画线方法一:利用SDK全局函数实现视图窗口画线功能
//获取设备描述表
HDC hdc;
//调用全局函数获得当前窗口的设备描述表,CWnd::m_hWnd根据继承原理,CDrawView继承了CWnd类的数据成员
hdc = ::GetDC(m_hWnd);
//移动到线条的起点
MoveToEx(hdc,m_ptOrigin.x,m_ptOrigin.y,NULL);//第四个参数用于保存鼠标移动前的位置,此处不需要,设为NULL
//画线
LineTo(hdc,point.x,point.y);
//释放设备描述表
::ReleaseDC(m_hWnd,hdc);
画线方法二:利用MFC的CDC类实现画线功能
说明:CDC类封装了所有与绘图相关的操作
CDC* pDC = GetDC();//定义CDC类型的指针,利用CWnd类的成员函数GetDC获得当前窗口的设备描述表对象的指针
pDC -> MoveTo(m_ptOrigin);//利用CDC类的成员函数MoveTo和LineTo完成画线功能
pDC -> LineTo(point);
ReleaseDC(pDC);
画线方法三:利用CClientDC类
说明:此类派生于CDC类,在构造时调用GetDC()函数,在析构时调用ReleaseDC()函数,因此无需显示调用这两个函数。
//CClientDC dc(this);//在当前视图窗口画线方法
CClientDC dc(GetParent());//获取当前视图窗口的父窗口,可以在父窗口画线
dc.MoveTo(m_ptOrigin);
dc.LineTo(point);
画线方法四:利用CWindowDC类
//CWindowDC dc(this);//只能在视类中画线
CWindowDC dc(GetParent());//可以在父窗口中画线
dc.MoveTo(m_ptOrigin);
dc.LineTo(point);
如果我们要更多功能的绘制方法,可以利用更多的资源和方法,如:
更多方法之:绘制彩色线条(设备描述表中默认有一个黑色画笔)
CPen pen(PS_SOLID,5,RGB(255,255,0));//创建画笔对象
CClientDC dc(this);
CPen* pOldPen = dc.SelectObject(&pen);
dc.MoveTo(m_ptOrigin);
dc.LineTo(point);
dc.SelectObject(pOldPen);
更多方法之:绘制连续线条
此时需要添加鼠标移动消息响应函数OnMouseMove,当鼠标移动时记录位置并绘制短线,然后需要将此时鼠标位置设置为下一次绘制的起点坐标,
这样便可以绘制连续线条了。为此,添加一个判断是否在画线的布尔变量m_bTrue,在视类构造函数中初始化为true,在OnLButtonDown中初始化为true,
在OnLButtonUp中初始化为false,OnMouseMove函数如下:
CClientDC dc(this);
//创建一个红色的、宽度为1的实线画笔
CPen pen(PS_SOLID,1,RGB(255,0,0));
//把创建的画笔选入设备描述表
CPen *pOldPen = dc.SelectObject(&pen);
if(m_bTrue == true)
{
dc.MoveTo(m_ptOrigin);
dc.LineTo(point);
m_ptOrigin = point;//如果不修改起点 坐标,画线效果是扇形
}
//恢复设备描述表
dc.SelectObject(pOldPen);
这样就可以绘制连续线条了。
更多方法之:使用画刷绘图
//创建一个红色画刷
CBrush brush(RGB(255,0,0));
//创建并获得设备描述表
CClientDC dc(this);
//用红色画刷填充鼠标拖动过程形成的矩形区域
dc.FillRect(CRect(m_ptOrigin,point),&brush);
更多方法之:位图画刷
注:需要先添加一个位图资源,ID为IDB_BITMAP1
//创建位图对象
CBitmap bitmap;
//加载位图资源
bitmap.LoadBitmapW(IDB_BITMAP1);
//创建位图画刷
CBrush brush(&bitmap);
//创建并获得设备描述表
CClientDC dc(this);
//用位图画刷填充鼠标拖动过程形成的矩形区域
dc.FillRect(CRect(m_ptOrigin,point),&brush);