CT 系统参数标定及反投影重建成像-2017数模国赛论文A298编程分析

CT 系统参数标定及反投影重建成像-2017数模国赛论文A298编程分析

之前的同学已经讲解清楚了这篇论文建模的主要思路，我主要讲解代码对建模思路的实现。

本文提到的论文下载地址：http://dxs.moe.gov.cn/zx/qkt/sxjm/lw/2017qgdxssxjmjslwzs/

---

一、读题-快速数据可视化

首先，论文中巧妙地使用Excel作为数据可视化的工具，如下引文：

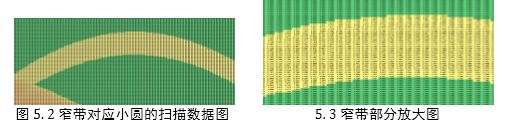
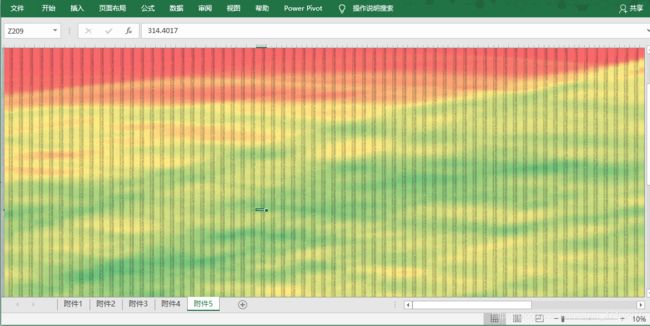
首先，我们在 Excel 中使用条件格式对数据进行了整体分析，附件 2 中非零的数据 进行标记，将数据中为零的数据与非零数据进行区分，缩放后得到了如下图形：

…… ……

…… ……

这种方法虽然简单，但有如下优点：

• 读题时，我们看到题目的数据时第一眼就是Excel。该篇文章巧妙地使用的Excel的条件格式功能，直观的让我们知道数据的内容，有助于前期读题的效率提升，在刚拿到数据时对数据产生直观判断。
• 另一个优点是可以直接在可视化的视图中选取原始数据，做一些初步的数据分析。这是MATLAB中所不太方便的。

以下是使用这种方法审阅数据的一个示意：

这启发我们不限制与只用MATLAB等软件分析处理数据的思维。更进一步，在比赛过程中，按照实际情况，应以效度和信度为准则，突破传统思维，发散性地运用工具。

二、模型建立与求解

问题一中的计算探测机间距d、确定增益函数、确定180个角度部分论文附录并未给出具体代码，而且程序实现比较简单，故不作讲解。

题目所示模型看起来非常复杂，对我们来说是一个全新的领域。但是只要知道了CT扫描问题的常用解法是拉东变换，知道了MATLAB有工具箱函数iradon就可以轻松实现逆拉东变换，这样子就可以为我们优化和处理其他问题节约出大量时间。同时建模时使用的均值滤波、自适应滤波（维纳滤波）、中值滤波，在MATLAB中都有直接的函数可以使用（medfilt2、wiener2、 filter2），这些函数的使用方法和原理在MATLAB的帮助文件中有详尽的介绍。

• A298中代码的体现：

% 逆拉东变换
img_1=iradon(data2,theta,512,'Hann');

% 这三列数据用来计算去噪后的误差值，比较各个去噪函数的优劣
img_1= medfilt2(img_1);
img_1= wiener2(img_1,[3 3]);
img_1= filter2(fspecial('average',3),img_1);

• 这几行代码就能初步地完成二三题的题解：

% iradon
clear
load theta.mat

load data2.mat
I1 = iradon(data2,theta,512,'Hann');
imshow(I1,[])

load data3.mat
I2 = iradon(data3,theta,512,'Hann');
imshow(I2,[])

load data5.mat
I3 = iradon(data5,theta,512,'Hann');
imshow(I3,[])

MATLAB代码运行示范

知道了这些，看似非常复杂陌生的模型就变得简单了，模型的核心内容已经完成，剩下的就是优化和完善的工作了。

---

这启发我们要善于使用已有的“轮子”，不盲目地去实现代码，能节省大量的时间，更能拓展思路。当然有时间和能力的话，如果觉得轮子不太优秀，也可自己去优化和重写：

比如另一篇范文A053中，编程队员是直接改动了MATLAB的库函数来实现了优化效果，引用如下：

在滤波反投影解算过程中，我们以 MATLAB 库函数iradon 和 radon 为基础， 根据需要对库函数做了相应的改动，具体的改动在支撑材料 iradon_reveise 函数 中已经标出。在求解时适时对函数的各个参数进行了修正，使得结果更为精确。

他们根据需要改变了库函数来适应与他们的模型

比如另一篇论文A090中把逆拉东变换离散化修正建立了ART模型，引用如下：

由于 FBP（滤波反投影）算法具有的缺陷与限制，对于不完全的投影数据，可以使用迭代法进行重建，这类算法在求解时把图像离散化。**ART（代数迭代法）**是常用的一种算法，其求解速度相对较快，结果较优，并且在求解过程中可以使用先验信息对数据进行修正。

该模型直接把问题转化为一组线性方程组，用代数迭代法的方法求解该方程组，便于理解且代码效率更高。

---

三、代码呈现

该论文的代码注释十分完善，可读性强；

但是呈现在论文中没有进行排版（缩进和高亮），且未呈现完整代码。

---

总结代码优缺点

• 优点
  • 注释完整
  • 使用库函数简化工作
• 缺点
  • 未放出完整代码
  • 论文中代码无排版

另外，在代码书写方面，代码封装性差（野数字多），且并行度低（使用MATLAB语言特性少）。但考虑到竞赛时间紧张，也没多大关系。

---

附录

以下我把论文所附代码追加了注释，在不影响实现的情况下对其部分代码进行了优化，对论文中未给出的代码进行了补全，附在下面：

clear
%数据读取
data1 = readmatrix("A题附件.xls",'Sheet','附件1');
data2 = readmatrix("A题附件.xls",'Sheet','附件2');
data3 = readmatrix("A题附件.xls",'Sheet','附件3');
data4 = readmatrix("A题附件.xls",'Sheet','附件4');
data5 = readmatrix("A题附件.xls",'Sheet','附件5');

save data1.mat data1
save data2.mat data2
save data3.mat data3
save data4.mat data4
save data5.mat data5

clear,clc
% 此程序用来求解第二问与第三问的反投影图以及 10 个点的吸收率

load data1.mat
load data2.mat
load theta.mat
load data3.mat
load data5.mat

% 此块程序利用模板反演进行校正
xc=0;yc=0;d=0.2776;
img_1=iradon(data2,theta,512,'Hann');
m=size(img_1,1);

% 这三列数据用来计算去噪后的误差值，比较各个去噪函数的优劣
img_1= medfilt2(img_1);
% img_1=wiener2(img_1,[3 3]);
% img_1=filter2(fspecial('average',3),img_1);

% 绘制附件二中的数据大小分布图;
figure(1)
imagesc(data2)

figure(2)
hold on
%绘制反投影图像
imagesc([-m/2 m/2],[m/2 -m/2],img_1)
%绘制旋转中心
plot(xc,yc,'xg')
% 原旋转中心坐标为（-9.2996,5.5520），由xzzx得出
dxc = 9.2996;
dyc = -5.5520;
% 绘制原正方形托盘的边框
plot(([-50 50 50 -50 -50]+dxc)/d,([-50 -50 50 50 -50]+dyc)/d,'r')
% 绘制原正方形托盘几何中心
plot(33.5,-20,'or')
% 绘制大正方形托盘的边框
plot([-256 256 256 -256 -256],[-256 -256 256 256 -256],'green')


%% 求解计算机与题目所给数据的比例系数

%取出原正方形托盘边框内的图像进行绘制
RED_1=img_1(96:455,110:469);

% k为所求比例系数
k=mean(data1,'all')/mean(RED_1,'all');
RED_1=RED_1.*k;
% 降低上图的像素
red_1=imresize(RED_1,256/360);

% 绘制经比例系数放大后的模板的反演图
figure(4)
imagesc(red_1)

%% 同第一图部分 绘制问题二的图
img_2=iradon(data3,theta,512); 
img_2=wiener2(img_2,[3 3]);
m=size(img_2,1);
figure(5),plot([-256 256 256 -256 -256],[-256 -256 256 256 -256],'r')
hold on
imagesc([-m/2 m/2],[m/2 -m/2],img_2)
plot(xc,yc,'ok')
plot(([-50 50 50 -50 -50]+dxc)/d,([-50 -50 50 50 -50]+dyc)/d,'r')
RED_2=img_2(96:455,110:469).*k;
% figure(6),imagesc(RED_2)
red_2=imresize(RED_2,256/360);
% 将矩阵中小于 0 的项变为 0;
red_2(red_2<0)=0; 
figure(7),imagesc(red_2)	

%% 同第一图部分 绘制问题三的图
img_3=iradon(data5,theta,512);
%对数据进行维纳滤波，减少噪声的影响
img_3=wiener2(img_3,[3 3]);

m=size(img_3,1);
figure(8)
plot([-256 256 256 -256 -256],[-256 -256 256 256 -256],'r')
hold on
imagesc([-m/2 m/2],[m/2 -m/2],img_3)
plot(xc,yc,'ok')
plot(([-50 50 50 -50 -50]+dxc)/d,([-50 -50 50 50 -50]+dyc)/d,'r')
RED_3=img_3(96:455,110:469).*k;
red_3=imresize(RED_3,256/360);

% 将矩阵中小于 0 的项变为 0;
red_3(red_3<0)=0;

figure(10),imagesc(red_3)

%% 误差计算
cha_1=abs(red_1-data1); s_1=sum(sum(cha_1));
wucha=s_1/256/256
% 算特殊值的结果
xishoulv2=[red_2(210,25),red_2(192,88),red_2(172,111),red_2(63,115),red_2(114,125),red_2(63,128),red_2(61,143),red_2(162,167),red_2(210,203),red_2(145,252)]
xishoulv3=[red_3(210,25),red_3(192,88),red_3(172,111),red_3(63,115),red_3(114,125),red_3(63,128),red_3(61,143),red_3(162,167),red_3(210,203),red_3(145,252)]

% 此程序用来求解一系列间距 d 产生的归一化方差结果在变量 fc 中
clc
clear
load data1
load data2
load theta
xc=0;
yc=0;
fc = zeros(37,2);
for i=1:37
    % 相邻两线间距
    d=0.2758+0.0001*i;	
    zd=sum(data2>0);
    [val1,wz1]=max(zd);
    [val2,wz2]=min(zd);
    num=find(data2(:,wz1)>0);
    y=(256-(max(num)+min(num))/2)*d;
    num=find(data2(:,wz2)>0);
    num=num(num>100);
    x=-(256-(max(num)+min(num))/2)*d;
    img_1=iradon(data2,theta,512,'Hann');
    m=size(img_1,1);
    x1=-x/d;
    y1=-y/d;
    xx=round(256-(50+x)/d); 
    yy=round(256-(50-y)/d);
    RED_1=img_1(yy:yy+359,xx:xx+359);
    k=mean(data1,'all')/mean(RED_1,'all');
    RED_1=RED_1.*k;
    % 降低上图的像素
    red_1=imresize(RED_1,256/360);	
    fc(i,1)=d; 
    fc(i,2)=dIF(red_1,data1);
end
fc

function [result]=dIF(img1,img2)
%dIF 此函数用来计算两个图像的归一化均方差
% 其中 img1 为重建后的图像 img2 为原图像
c=img1-img2;
c=c.^2; 
d=img2.^2; 
h=sum(sum(c));
hm=sum(sum(d)); 
result=1-h/hm;
end

% 导入theta
clear
theta = [-60.2152,-58.8587,-58.3008,-57.2081,-56.1751,-55.2026,-54.1989,-53.1945,-52.1913,-51.1883
    -50.1841,-49.1784,-48.1748,-47.1711,-46.167,-45.0092,-44.1559,-43.1498,-42.1464,-41.1399
    -40.1346,-39.1288,-38.1194,-37.1142,-36.1026,-35.094,-34.0861,-33.08,-32.0708,-31.0575
    -30.0481,-29.1362,-28.0209,-27.0104,-25.9942,-24.9819,-23.9634,-22.9444,-21.9239,-20.9011
    -19.8815,-18.8563,-17.8288,-16.799,-15.7555,-14.7159,-13.6685,-12.6137,-11.5409,-10.4695
    -9.373,-8.2484,-7.1066,-5.8943,-4.5786,-3.0205,-2.5839,-2.1474,-1.7108,-1.2742
    -0.8377,-0.4011,0.0354,0.472,0.9085,1.3451,3.5747,4.8814,6.2408,7.4525
    8.5643,9.73211,10.7974,11.844,12.9171,13.989,15.0196,16.0352,17.1078,18.1144
    19.1525,20.1918,21.2181,22.2248,23.2439,24.2613,25.1502,26.2951,27.1125,28.3244
    29.33,30.3405,31.3545,32.3644,33.3739,34.3827,35.3912,36.3992,37.4067,38.4139
    39.4208,40.4272,41.5339,42.4392,43.4449,44.4501,45.4553,46.4601,47.465,48.4692
    49.4734,50.4776,51.4813,52.485,53.4886,54.4919,55.4949,56.498,57.5007,58.5034
    59.5059,60.5081,61.5102,62.512,63.5138,64.5152,65.5166,66.5176,67.5183,68.5188
    69.5188,70.5186,71.5179,72.5168,73.5151,74.5128,75.5097,76.5056,77.5004,78.4938
    79.4853,80.4743,81.4601,82.4415,83.4162,84.3812,85.3301,86.2507,87.1162,87.8583
    88.3061,91.7791,92.3391,93.1286,94.0144,94.9453,95.8998,96.868,97.845,98.8278
    99.8147,100.8045,101.7966,102.7904,103.7858,104.7818,105.7789,106.7768,107.7753,108.7744
    109.7738,110.7737,111.7741,112.7745,113.7751,114.7763,115.7775,116.7791,117.7812,118.7725 ]';



theta = theta(:)+90;
save theta