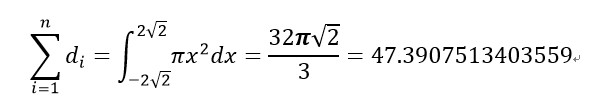校赛C题题解

http://acm.sdut.edu.cn/sdutoj/problem.php?action=showproblem&problemid=2617

思想是向中位数移动。详见代码，下面是证明（即为何向中位数移动总和最少）

抽象，并普遍化：

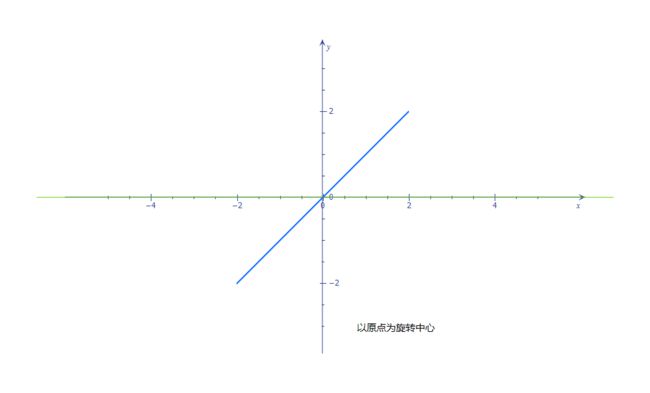
证明，一条直线，以中点为圆心和以非中点为圆心，旋转，求各点旋转路径之和。

法一：在直角坐标系下，

对于任意一点，其移动距离可表示为：

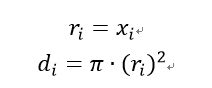
故各点运动距离的和为：

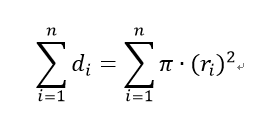
由积分定义知：

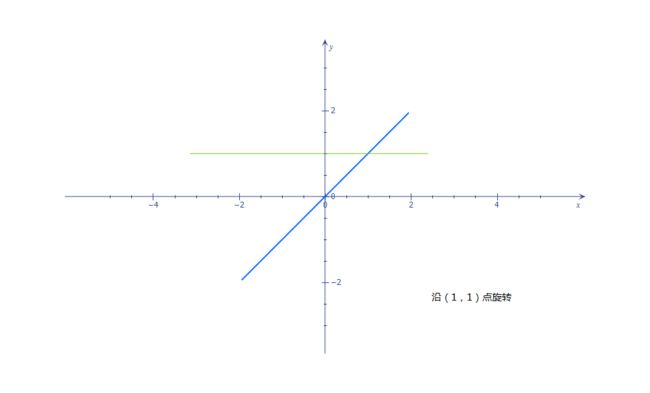
同理，为简化运算，将图二坐标系向右，向上均移动一个单位，得：

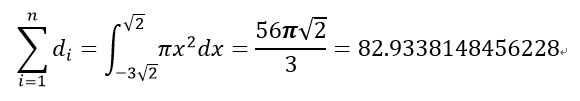
法二：利用极坐标系，详解不写了

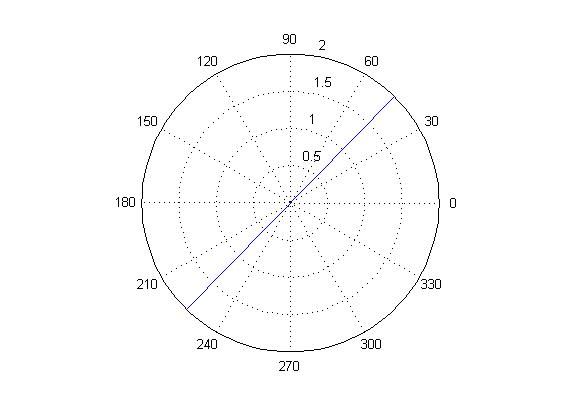
法三：初等数学方法

各点移动距离之和就是其扫过面积，故在中点处时旋转扫过面积一定小于非中点旋转扫过面积。

 

综上，C题可采用移动到中位数位置作为最短移动。

证毕。

以下是代码：

#include 
#include 
#include 
#include 

using namespace std;

#define mytype long long int

int main()
{
    int n, m, d;
    while(cin>>n>>m>>d && (n || m || d))
    {
        vector a;
        mytype t = n * m;
        mytype const_of_number = n * m;
        while(t--)
        {
            mytype temp;
            cin>>temp;
            a.push_back(temp);
        }

        mytype middle = const_of_number / 2;
        //sort(a.begin(),a.end());

        random_shuffle(a.begin(),a.end());
        nth_element(a.begin(),a.begin()+middle,a.end());

        vector::iterator it = a.begin();
        vector::iterator it_middle = a.begin() + middle;

        mytype count_of_steps = 0;

        mytype flag = 0;

        for(; it != a.end(); ++it)
        {
            if( (abs(* it - *it_middle)) % d == 0 )
            {
                count_of_steps += (abs(( *it - *it_middle))) / d;
            }
            else
            {
                flag = 1;
                break;
            }
        }

        if(flag)
        {
            cout<<-1<