图论——寻找无向连通图割点算法

查看原文：http://www.wyblog.cn/2016/12/20/%e5%9b%be%e8%ae%ba-%e5%af%bb%e6%89%be%e6%97%a0%e7%9b%b8%e8%bf%9e%e9%80%9a%e5%9b%be%e5%89%b2%e7%82%b9%e7%ae%97%e6%b3%95/

割点定义

首先，如果一个连通的无向图中的任意顶点删除之后，剩下的图如果仍然连通，那么这样的无向图称为是双连通的。如果一个图不是双连通的，那么，将其删除后图将不再连通的那些顶点叫做割点。 割点在实际应用中是很重要的，割点越少的系统显然越可靠，例如对于公共运输系统，如果不存在割点，那么当任意一个节点出现问题时，我们总可以找到另一条运输路径。

例子

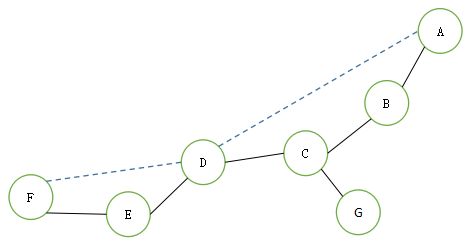以下例子引用《数据结构与算法分析》教材。 对于上图，C与D为其割点。当断开C，顶点G则与原图不连通。若断开D，顶点E、F与原图不再连通。 对其进行深度优先遍历，则能够导出其深度优先树： 图中虚线为背向边，表示的是遍历的是已知定点。

算法

根据割点的描述，首先可以想到一种暴力破解法。可以遍历每一个顶点，若当前顶点去掉之后，如果图不再连通，那么当前顶点就是一个割点，若不是割点，则将当前点恢复到图里。此算法涉及到所有顶点个数次DFS来判断图是否还连通，所以其复杂度为O（V*（V+E）），其中V为顶点个数，E为边的条数。 以上算法复杂度较高，在《数据结构与算法分析》教材里给出了一个厉害的算法，只用了一次深度优先搜索，便将割点给寻找出来了，具体做法如下。

1. 首先定义一个Num[V]数组，用于深度优先遍历时对树顶点进行编号。
2. 接着定义Low[V]数组，此数组记录的是顶点V能通过其子顶点或者子顶点的一条背边，所能达到的最低顶点编号。
3. 另外，在程序里还会定义几个辅助数组，Visit[V]用来标记顶点V是否被遍历到了，Parent[V]用于记录顶点V的父节点，isArt[V]用于记录顶点V是否已经被断定为割点了(避免重复输出)。

根据以上方式，可以得到上边例子里被编号的顶点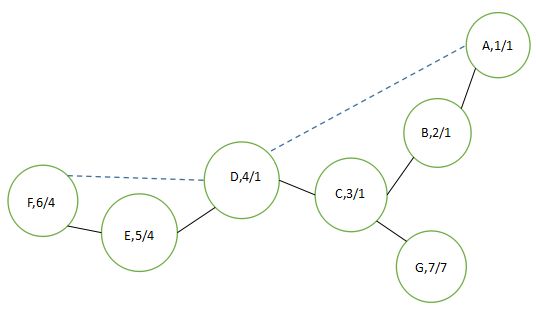： 圈里的数字分别为顶点的Num[v]与Low[V]。 计算Num[V]的方法很简单，就是经过一次先序深度优先遍历，就能对顶点编号了。 计算Low[V]复杂一些，采用的是后序深度优先遍历。根据Low[]数组的定义，可知顶点V的Low[V]值实际上以下三种情况中的最小值。

1. 顶点V的Num[V]
2. 顶点V的所有背向边（v，w）中的最低Num[W]
3. 顶点V的所有邻接边（v，w）中的最低Low[V]

只有第三种情况需要提前知道邻接顶点的Low[V]值，所以需要后序遍历，从叶子节点到根倒推回来。而第一二种情况是在先序遍历时就能编号的。 然而，对于先序遍历与后序遍历的区别，就在于递归语句的位置。执行语句在递归语句之前，则是先序遍历；执行语句在递归语句之后，则是后续遍历。基于此，先序遍历与后续遍历就能同时存在于程序段里了。 对于任何顶点V，它是割点当且仅当它有某个儿子w，使得 Low[W] ≥ Num[V]。 想一想为什么？ 实际上，Low[W]代表的是顶点W能通过或者不通过一条回边而达到另外顶点的Num[]值中的最小一个。若 Low[W] ≥ Num[V] ，w是v的子节点，那就说明w通过前向通路回不到v的父节点以及祖先节点，那么去掉v过后，w将被孤立，所以v是割点。

算法缺点

此算法有一个小缺点，那就是根所在的顶点，无论如何它都是满足 Low[W] ≥ Num[V] 的，所以对于根需要特殊检验。可以预见，当根是割点时，在深度优先树里，它一定有不止一个儿子，当断开根时，树则变为了森林。所以，在程序里，会有一个children变量，来记录每个顶点的儿子个数，然后去检查根有多少儿子，如果超过一个，那么根也是割点。

代码

最后附上完整代码。

#include< cstdio>
#include< iostream>
#include< queue>
#include< algorithm>

using namespace std;

#define MAX_VERTEX_NUM 100

int Counter;
int Visit[MAX_VERTEX_NUM]; //标记是否被访问过 
int Num[MAX_VERTEX_NUM];
int Low[MAX_VERTEX_NUM]; //记录从当前顶点通过树边跟一条背向边能达到的最低顶点编号 
int Parent[MAX_VERTEX_NUM];
int isArt[MAX_VERTEX_NUM]; //用于标记是否已经被输出为割点了 

void Init_Globalpara(void)
{
    Counter=1;
    memset(Visit,0,sizeof(Visit));
    memset(Num,0,sizeof(Num));
    memset(Low,0,sizeof(Low));
    memset(Parent,0,sizeof(Parent));
    memset(isArt,0,sizeof(isArt));
}

typedef struct EdgeNode
{
    int adjVertex;
    EdgeNode *nextEdgeNode;
}EdgeNode;

typedef struct VerNode
{
    int data;
    EdgeNode *firstedge;
}VerNode;

typedef struct Graph
{
    VerNode verNode[MAX_VERTEX_NUM];
    int vertex_num,edge_num;
}Graph;

void CreateDAG(Graph &G,int n,int e)
{
    int k;
    char v,i,j;
    G.vertex_num=n;
    G.edge_num=e;
    EdgeNode *p;

    for(k=1;k<=n;k++)
    {
        cin>>v;
        G.verNode[k].data=(v-'A'+1);
        G.verNode[k].firstedge=NULL;
    }
    for(k=1;k<=e;k++) //创建无向图
    {
        cin>>i>>j;

        p=new EdgeNode;
        p->adjVertex=(j-'A'+1);
        p->nextEdgeNode=G.verNode[i-'A'+1].firstedge;
        G.verNode[i-'A'+1].firstedge=p;

        p=new EdgeNode;
        p->adjVertex=(i-'A'+1);
        p->nextEdgeNode=G.verNode[j-'A'+1].firstedge;
        G.verNode[j-'A'+1].firstedge=p;
    }
}

void FindArt(Graph &G,char Vert) //一次DFS搞定，复杂度O(V+E)，前序遍历后序遍历混合使用 
{
    int children=0;
    int Vnum=(Vert-'A'+1);
    EdgeNode *w;
    w=G.verNode[Vnum].firstedge;
    Visit[Vnum]=1;

    Low[Vnum]=Num[Vnum]=Counter++; //CASE1 

    while(w)
    {
        int Wnum=w->adjVertex;
        if(!Visit[Wnum])
        {
            children++;
            Parent[Wnum]=(Vert-'A'+1);
            FindArt(G,char(Wnum-1+'A'));
            //考虑根是否为割点，当且仅当深度优先树的根有不止一个儿子时，根才为节点 
            if(Parent[Vnum]!=0 && Low[Wnum]>=Num[Vnum] && !isArt[Vnum])
            {
                isArt[Vnum]=1;
                cout<1)
            {
                isArt[Vnum]=1;
                cout<nextEdgeNode;
    }
}

int main()
{
    Graph G;
    Init_Globalpara();
    CreateDAG(G,7,8);
    FindArt(G,'A');
}

/**************
A B C D E F G
A B
B C
C G
C D
D E
E F
F D
D A
输出：
D is an articulation point.
C is an articulation point. 
**************/

查看原文： http://www.wyblog.cn/2016/12/20/%e5%9b%be%e8%ae%ba-%e5%af%bb%e6%89%be%e6%97%a0%e7%9b%b8%e8%bf%9e%e9%80%9a%e5%9b%be%e5%89%b2%e7%82%b9%e7%ae%97%e6%b3%95/